ВОПРОСЫ ПО КЛАССИЧЕСКОМУ ВАРИАЦИОННОМУ ИСЧИСЛЕНИЮ.
Основные понятия вариационного исчисления: функционал, непрерывный функционал, линейный функционал, вариация функционала.	1
Основные понятия вариационного исчисления: функционал, сильный и слабый экстремум функционала, условия экстремума.	2
Формировка простейшей вариационной задачи классического вариационного исчисления. Вывод уравнение Эйлера.	3
Вывод уравнение Эйлера. Основная лемма вариационного исчисления.	3
Функционалы, зависящие от высших производных: уравнение Эйлера - Пуассона, условие Лежандра.	5
Задачи на условный экстремум: метод множителей Лагранжа.	7
Вариационные изопериметрические задачи. Особенности их решения.	9
Функционалы, зависимые от многих функций: уравнения Эйлера, условие Лежандра.	11
Применение классического вариационного исчисления к задаче оптимального управления, двухточечная краевая задача.	12
Применение классического вариационного исчисления к задаче оптимального управления, уравнения Эйлера - Лагранжа в канонической форме.	12
ВОПРОСЫ ПО НЕКЛАССИЧЕСКОМУ ВАРИАЦИОННОМУ ИСЧИСЛЕНИЮ
Определение функции Гамильтона, вспомогательные переменные, их смысл.	14
Понятия игольчатой вариации управления, принцип максимума Л. С. Понтрягина.	15
Применение принципа максимума к объектам с линейным вхождением сигнала управления, двухточечная краевая задача.	17
Вид управления оптимального по быстродействию, теорема об n-интервалах.	19
Структура управления оптимального по быстродействию, определение моментов переключения.	22
Структура управления оптимального по быстродействию, определение знака управления на первом интервале.	25
Принцип оптимальности, понятие функции Беллмана.	26
Функция Беллмана, вывод функционального уравнения Беллмана.	28
Функциональное уравнение Беллмана, техника определения оптимального управления в методе динамического программирования.	30
Техника определения оптимального управления в методе динамического программирования, достоинства и недостатки динамического программирования.	31
ВОПРОСЫ ПО ТЕОРИИ АКОР
Постановка задачи управления Летовым А. М., ее решение методом динамического программирования.	32
Постановка задачи АКОР для линейных многомерных объектов, вывод уравнения Риккати.	34
Постановка нелинейной задачи АКОР, метод степенных рядов в ее решении.	36
Критерий обобщенной работы, основная теоремы Красовского А. А.	38
Основная теорема Красовского А. А., особенности применения метода синтеза систем управления по критерию обобщенной работы к линейным объектам.	40
Основные понятия адаптивного управления. Адаптивная система со стабилизацией частотной характеристики разомкнутого объекта.	42

Основные понятия вариационного исчисления: функционал, непрерывный функционал, линейный функционал, вариация функционала.

Задача синтеза оптимальных систем в конечном счете сводится к отысканию вектора U(t) управления, обеспечивающего экстремальное (т. е. минимальное или максимальное) значение некоторого критерия качества – некоторого функционала. Как известно, методы отыскание экстремальных значений функционалов составляют основу вариационного исчисления.

1. Переменная величина V называется функционалом, зависящим от функции x(t) V = V[x(t)], если каждой функции из некоторого класса соответствует значение V, т. е. функции x(t) соответствует число V.

Пример 1: .

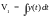Набору функций e^-t/T1, e^-t/T₂ , …, e^-t/T_n будут соответствовать числа , …, _.

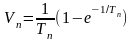Пример2: функционал зависит не только от функции , но и ее производной x(t). Известно, что длина кривой x(t) сое диняющей на плоскости x, t точки t=0, x=0 и t=1,x=1 будет равна интегралу 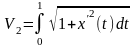; x^’(t)=

2. Приращением или вариацией x аргумента x(t) функционала V[x(t)] называется разность между двумя функциями , причем x(t), x₁(t) .

3. Функционал V[x(t)] называется непрерывным, если малому изменению x(t) cоответствует малое изменение функционала V[x(t)].

3a) Функционал V[x(t)] непрерывен при x₀(t) в смысле близости k-го порядка, ес ли для любого можно подобрать такое 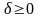, что |V[x(t)-V[x₀(t)]| 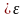при , ,- - - - - - - .

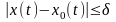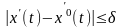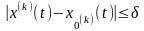4. Линейным функционалом называется функционал L[x(t)], удовлетворяющий условиям: L[C*x(t)] =C*L[x(t)], где С - произвольная постоянная, и L[x₁(t)+x₂(t)]=L[x₁(t)]+L[x₂(t)]

Примером является

5. Если приращение функционала V = V[x(t)+x]-V[x(t)] можно представить в виде V=L[x(t),x]+B(x(t),x)*(x+x,x), где L[x(t),x] – линейный по отношению к x функционал, и B(x(t),x)0 при (x+x,x)0, то линейная по отношению x часть приращения функционала, т.е. L[x(t),x], называется вариацией функционала и обозначается V.

6. Теорема. Если функционал V[x(t)], имеющий вариацию, достигает минимума при x₀(t), где x₀(t) – внутренняя точка области определения функционала, то V = 0.

Если V0, то при достаточно малом расстоянии (x+x,x) знак правой части совпадает со знаком V, но V меняет знак при изменении знака x вследствие линейности, следовательно, при достаточно малом (x+x,x) и знак V изменяется при изменении знака x, т.е. при x₀(t) не достигается ни макс, ни мин. Т.о., необходимым условием экстремума функционала явл. V=0.

Основные понятия вариационного исчисления: функционал, сильный и слабый экстремум функционала, условия экстремума.

Переменная величина V называется функционалом, зависящим от функции x(t) V = V[x(t)], если каждой функции из некоторого класса соответствует значение V, т. е. функции x(t) соответствует число V.Пример: ; Набору функций e^-t/T1, e^-t/T₂ , …, e^-t/T_n будут соответствовать числа , …, _.

Функции, обеспечивающие экстремум функционала, называются экстремалями.

По определению функционал V[x(t)] достигает на кривой x₀(t) минимума, если его значение на любой, достаточно близкой к х₀(t) кривой не меньше, чем V[x₀(t)], т.е. V = V[x(t)] - V[x₀(t)] = 0. Говоря о максимуме или минимуме функционала, мы подразумеваем наибольшее или наименьшее значение функционала по отношению к его значениям на близких кривых, но близость кривых может быть понимаема различно. Так например, если значение функционала на некоторой кривой меньше, чем на всех других допустимых кривых, близких в смысле близости нулевого порядка, то говорят, что на этой кривой достигается сильный минимум.

Если же на кривой х₀(t) достигается минимум по отношению к более узкому классу (множеству) кривых, для которых не только модуль разности 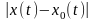мал, но мал также и , т.е. имеет место близость первого порядка, то минимум называется слабым.

Подчеркнем, что сильный минимум является одновременно и слабым, но не наоборот. Необходимо отметить, что в сформулированной простейшей задаче вариационного исчисления определяется слабый минимум. И вообще для классического вариационного исчисления характерно в основном исследование задач на слабый экстремум функционалов. Условия сильного экстремума устанавливает принцип максимума Л.С. Понтрягина.

Если приращение функционала V = V[x(t)+x]-V[x(t)] можно представить в виде V=L[x(t),x]+B(x(t),x)*(x+x,x), где L[x(t),x] – линейный по отношению к x функционал, и B(x(t),x)0 при (x+x,x)0, то линейная по отношению x часть приращения функционала, т.е. L[x(t),x], называется вариацией функционала и обозначается V.

Теорема. Если функционал V[x(t)], имеющий вариацию, достигает минимума при x₀(t), где x₀(t) – внутренняя точка области определения функционала, то V = 0.

Если V0, то при достаточно малом расстоянии (x+x,x) знак правой части совпадает со знаком V, но V меняет знак при изменении знака x вследствие линейности, следовательно, при достаточно малом (x+x,x) и знак V изменяется при изменении знака x, т.е. при x₀(t) не достигается ни максимум, ни минимум. Таким образом, необходимым условием экстремума функционала является V=0.

Введенное понятие вариации функционала, как главной линейной части приращения, известное также как сильного дифференциала (диф. Фреше) функционала, относительно сложно вычислить. В связи с этим появилось понятие слабого дифференциала (дифференциала Гато) , где функция *(t) есть вариация аргумента x(t) и принадлежит тому же классу функций, что и x(t);  - параметр.Доказана теорема, что если существует сильный дифференциал функционала, то существует и слабый дифференциал (но не наоборот), причем в этом случае дифференциалы совпадают.