5. Законы распределения носителей в зонах полупроводника.

Для определения концентрации свободных носителей в зонах полупроводника необходимо знать число мест, на ко­торых могут находиться свободные носители, т. е. плотность квантовых состояний и вероятность заполнения этих мест — квантовых состояний — носителями. Плотность квантовых состояний — это число квантовых состояний, приходящихся на единичный интервал энергии в единичном объеме полупроводника. При нормальных усло­виях концентрация свободных носителей в зонах обычно много меньше плотности квантовых состояний в них. Поэто­му свободные носители занимают квантовые состояния лишь в узком энергетическом интервале около краев зон. Для кра­ев зон плотность квантовых состояний определяется уравне­нием:

(1.1)

где Е — энергия носителя; E_гр — энергия, соответствующая границе зоны; А — некоторая постоянная. В дальнейшем бу­дем считать A_C=A_V. Зависимость N(E) для краев зон показана на рис. 1.12.Вероятность заполнения квантовых состояний носителями определяется функцией распределения носителей по энергиям. Для электронов - частиц, подчиняющихся принципу Пау­ли, вероятность нахождения электрона на энергетическом уровне, соответствующем энергии E_F при некоторой темпера­туре Т определяется функцией распределения Ферми — Дира­ка, имеющей вид:

(1.2)

где E_F — уровень Ферми. Формально из уравнения (1.2) сле­дует, что уровень Ферми соответствует энергетическому уровню, вероятность заполнения которого при Т0 К равна 1/2, так как при Т>0 и E=E_F, f_n(E,T)=1/2. По физиче­скому смыслу энергия, соответствующая уровню Ферми, яв­ляется средней свободной энергией, приходящейся на один электрон при постоянной температуре. Отсюда следует важ­ное свойство уровня Ферми: в любой единой системе в со­стоянии термодинамического равновесия положение уровня Ферми постоянно. Ещё одно определение: положение уровня Ферми соответствует работе, которую необходимо затратить для изменения числа частиц на единицу. Уровень Ферми называют также химическим потенциалом.

Рис. 1.12. Зависи­мость плотности кван­товых состояний от энергии

Рис. Рис. 1.13. График функции распределе­ния Ферми — Дирака при различных тем­пературах

Рассмотрим основные свойства функции Ферми—Дирака. При Т=0К для E>E_F f_n(E, T)=0, т.е. все квантовые со­стояния с энергией, лежащей выше уровня Ферми, при Т=0 К будут свободны. При Т=0К для E<E_F f_n(E, T) =1, т.е. все квантовые состояния с энергией, лежащей ниже уровня Ферми, будут заняты электронами. Следовательно, для температур абсолютного нуля график функции распределения Ферми—Дирака имеет ступенчатый вид (рис. 1.13).При Т>0 и E<E_F f_n(E, T)<1, а при Т>0 и Е>Е_F f_n(E, T)>0, т. е. при Т выше абсолютного нуля появляется вероятность нахождения электронов на энергетических уров­нях, расположенных выше уровня Ферми, и вероятность их отсутствия на уровнях, расположенных ниже уровня Ферми. Причем эти вероятности тем больше, чем выше температура (рис. 1.13). Вероятность того, что энергетический уровень в валентной зоне не занят электроном, есть вероятность нахождения на этом уровне дырки. Так как сумма этих вероятностей есть событие достоверное, то для энергетических уровней в ва­лентной зоне:

(1.3)

Отсюда следует, что вероятность нахождения дырки в ва­лентной зоне на уровне с энергией Е при данной температу­ре Т равна:

(1.4)

На графике функции Ферми—Дирака для электронов и ды­рок совпадают, но имеют противоположные начала отсчета значений функций (рис. 1.13). Следует отметить, что функ­ция распределения Ферми—Дирака симметрична относитель­но уровня Ферми. В полупроводниковой электронике наиболее часто при­меняются полупроводники, для которых выполняется условие . В этом случае экспоненциальный член в знаменателе функции Ферми—Дирака оказывается намно­го больше единицы и эту функцию можно представить в виде:

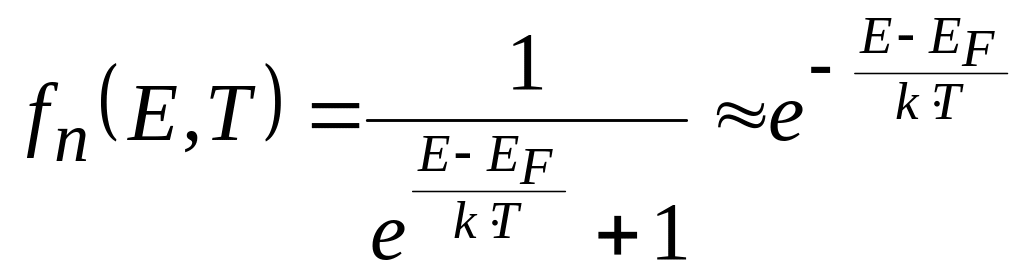(1.5,а)

(1.5,б)

При этом функция Ферми—Дираки переходит в функцию Максвелла—Больцмана, которая описывает распределение по энергиям классических частиц. Такая замена справедли­ва вследствие того, что при концентра­ция свободных носителей в зонах полупроводника оказыва­ется намного меньше плотности квантовых состояний в них. В этом случае принцип Паули теряет силу, так как вероят­ность попадания на один и тот же энергетический уровень более двух электронов при этих условиях становится очень малой. Замена функции Ферми—Дирака функцией Максвелла— Больцмана, когда это возможно, значительно упрощает рас­четы концентрации свободных носителей и анализ ее зави­симости от различных факторов.