12. Факторы, определяющие подвижность носителей.

определяется средней скоростью дрейфа носителей.

Эта скорость зависит от интенсивности рассеивания носителей в кристаллической решётке полупроводника. Это рассеивание в основном происходит на тепловых колебаниях атомов решётки и ионизированных атомов примеси.

Пусть - подвижность, обусловленная только рассеиванием на тепловом колебании решётки. При увеличении температуры амплитуда колебаний увеличивается. Рассеивание носителей увеличивается и - уменьшается с ростом температуры по закону

.

Рассеивание носителей на ионах примеси вызывается взаимодействием заряженных носителей с полем ионов. Подвижность, обусловленная рассеиванием на ионах . Как известно, в широком диапазоне температур, все атомы примеси ионизованы, каждый ион создаёт вокруг себя кулоновское поле. Носители, пролетая мимо иона, попадают в область действия поля, и испытывают кулоновское рассеивание или отталкивание. В результате их траектория искривляется.

Р ис. Рассеивание на ионах примеси

Очевидно, чем выше температура, тем больше тепловая скорость носителей V, тем меньшее времени носители пребывают вблизи иона, тем меньше отклонение траектории его движения, то есть меньше его рассеивание. Поэтому увеличивается с ростом температуры:

.

Результирующая подвижность носителей находится с помощью соотношения:

.

П ри этом при низких температурах тепловые колебания малы, рассеяние на них мало, поэтому подвижность в основном растёт с увеличением температуры, так как растёт .При высоких температурах уменьшается с ростом температуры, так как - мало, а - уменьшается.

Рис. Зависимость подвижности от температуры

В области положительных температур уменьшается с ростом температуры. Электроны и дырки имеют неодинаковую подвижность, связано это с тем, что движение электронов в кристалле – это движение почти свободных частиц. Дрейф дырок – процесс поэтапного передвижения незаполненных ковалентных связей. Поэтому дырки больше «связаны» с кристаллической решёткой: и полупроводниковые приборы, использующие в качестве носителей электроны, а не дырки, могут работать на более высоких частотах.

Значения при T=300 К:

Ge: , .

Si: , .

GaAs: , .

13. Температурная зависимость удельной проводимости полупроводников.

Температурная зависимость удельной проводимости или удельного сопротивления полупроводников определя­ется температурной зависимостью концентрации носителей и их подвижности. В области естественных температур по­движность носителей уменьшается с ростом температуры, примерно подчиняясь зависимости:

(1.19)

где A —постоянный коэффициент. Уменьшение подвижности с ростом температуры объясняется увеличением рассеивания носителей на тепловых колебаниях атомов кристаллической решетки полупроводника. В примесных полупроводниках в достаточно широком температурном диапазоне концентрация свободных носите­лей тока в основном определяется постоянной концентрацией носителей примесного происхождения и ее изменение с тем­пературой малозаметно. Поэтому в области естественных температур температурная зависимость удельной проводи­мости примесных полупроводников почти полностью опреде­ляется слабой зависимостью подвижности от температуры (1.19), и с ростом температуры проводимость уменьшается, а удельное сопротивление возрастает. Однако при увеличе­нии температуры до критической температуры полупровод­ника Т_кр концентрация носителей собственного происхожде­ния начнет сравниваться с концентрацией носите­лей примесного происхож­дения, а при Т>Т_кр пре­вышать ее. В этом случае зависимость удельной проводимости от темпера­туры повторяет в основ­ном температурную зави­симость концентрации собственных носителей, которая определяется уравнением (1.11). Поэ­тому при Т>Т_кр проводи­мость полупроводника резко возрастает, а сопротивление уменьшается. Для нагляд­ности на рис. 1.19 показана зависимость удельного сопротив­ления германия n-типа от температуры при различной сте­пени легирования.

Следует отметить, что с повышением степени легирования полупроводника температурная зависимость его проводимо­сти и сопротивления ослабевает, так как уменьшается роль носителей собственного происхождения.

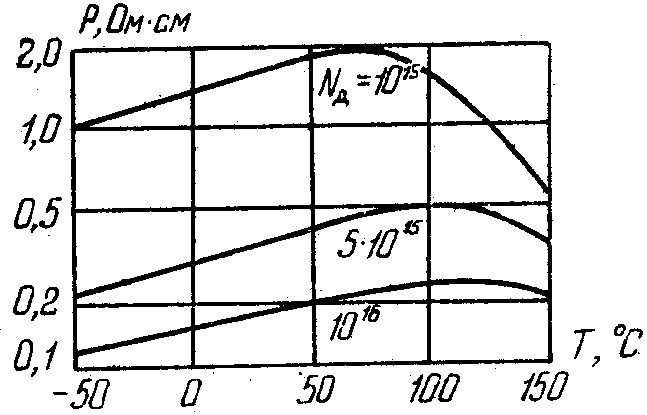
Рис. 1.19. Зависимость удельного сопро­тивления германия n-типа от темпера­туры при различных концентрациях до­норов. Кроме направленного дрейфового движения носителей под действием сил электрического поля, в полупроводниках могут существовать направленные потоки носителей, обус­ловленные градиентом концентрации носителей. Механизм появления таких потоков можно пояснить на двухмерной модели полупроводника с неоднородной концентрацией примеси, показанной на рис. 1.20, где градиенту концентраций носителей соответствует различное количество носителей в каждой точке х. Как уже отмечалось, при хаотичном тепло­вом движении носителей в отсутствие электрического поля перемещение каждого носителя в любом направлении равно­вероятно. Поэтому на рис. 1.20 половина носителей переме­щается по направлению х, а другая половина — встречно х.

Р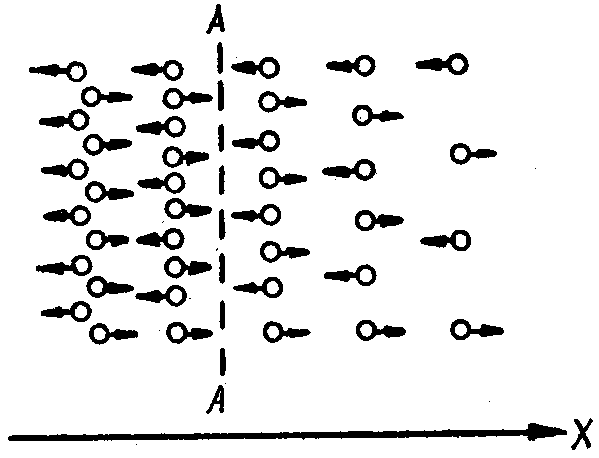 ис. 1.20. Картина появления на­правленных диффузионных потока носителей в неоднородном полупро­воднике

Движение носителей в на­правлениях, нормальных к оси х, для рассматриваемо­го случая можно не учиты­вать. Из рис. 1.20 видно, что наличие градиента концент­рации носителей приводит к тому, что из области их вы­сокой концентрации носите­лей уходит больше, чем из области их низкой концент­рации. Это неравенство по­токов носителей определяет существование направленного потока этих носителей (например, через плоскость А—А) в сторону уменьшения их концентрации. Всякое направленное движение носителей заряда есть электрический ток. Ток, обусловленный градиентом концен­трации носителей, называют диффузионным током, а само движение носителей под действием этого градиента — диф­фузионным движением носителей. Диффузионное движение носителей описывается уравне­ниями Фика. Согласно первому уравнению Фика, плотность потока носителей f пропорциональна градиенту их концен­трации, взятому с обратным знаком. Для одномерного случая:

где D_n — коэффициент пропорциональности, называемый ко­эффициентом диффузии. Численно D_n равен потоку носите­лей при единичном градиенте концентрации и имеет размер­ность см²/с.

Умножая величину плотности потока на величину заряда носителей, получаем плотность диффузионного тока. Для одномерного случая:

(1.20,а) (1.20,б)

Из уравнений (1.20, а, б) следует, что направление диффу­зионного тока отрицательных электронов совпадает с направ­лением возрастания их концентрации, а диффузионный ток положительных дырок направлен в сторону убывания их концентраций (рис. 1.21, а, б).

а)

б)

Рис. 1.21. Направление диффузионного тока, пере­носимого электронами (а) и дырками (б)

Величина коэффициента диффузии D, как и величина по­движности , определяется интенсивностью рассеивания но­сителей на тепловых колебаниях атомов кристаллической решетки. Поэтому эти две величины оказываются взаимно связанными. Эту связь устанавливает уравнение Эйнштейна: . (1.21)