Модель задачи о назначениях

i=m j=n

L( X ) = ∑ ∑c_ijx_ij->min;

i=1j=1

n

∑x_ij = 1 ( j = 1,n) (5.1)

j=1

m

∑x_ij = 1 ( i = 1,m),

i=1

х_ij ={0, 1}, i=1, j=1

Специфическая структура задачи о назначениях позволила разработать так называемый "Венгерский метод" ее решения. Поэтому, хотя в Excel такие задачи решаются обычным симплекс-методом, в лабораторной работе требуется построить модель задачи о назначениях вида (5.1). В некоторых случаях, например, когда c_ij - это компетентность, опыт работы, или квалификация работников, условие задачи может требовать максимизации ЦФ, в отличие от (5.1). В этом случае ЦФ L ( X) заменяют на L₁(X)=-L(X) и решают задачу с ЦФ L₁(X) ->min, что равносильно решению задачи с ЦФ L(X) ->max.

РЕКОМЕНДАЦИИ К РЕШЕНИЮ ЗАДАЧИ О НАЗНАЧЕНИЯХ

1. Процесс приведения задачи о назначениях к сбалансированному виду имеет свои особенности по сравнению с ТЗ. Если условие сбалансированности задачи (4.2) не выполняется из-за нехватки работ или исполнителей в количестве k_ab, то для создания баланса надо ввести такое же количество k_ab фиктивных строк или столбцов.

2. Особенностью решения данной задачи является моделирование системы предпочтений, сложившейся у руководства предприятия по описанному в условии задачи кадровому вопросу.

3. В задаче о назначениях увольнение прежнего сотрудника или непринятие на работу нового сотрудника моделируется попаданием единицы в фиктивный столбец матрицы решений задачи, поэтому для запрещения или разрешения таких ситуации необходимо использовать соответствующие "тарифы".

4. Значения "тарифов" c_ij^з выбираются в зависимости от направления

оптимизации ЦФ задачи о назначениях (L(X)→max или L(X)→min). При этом руководствуются принципом "невыгодности" запрещенных назначений. Так, если L(X) - это общая компетентность работников, то в качестве

запрещающих надо выбирать нулевые компетентности c_ij^з, А если L(X) - это общее время прохождения машинами транспортных маршрутов, то в качестве запрещающих надо выбирать значения c_ij^з, превосходящие по величине максимальные реальные значения c_ij.

5. При решении задач о назначении в Excel необходимо учитывать, что переменные x_ij являются булевыми.

18. Постановка задачи динамического программирования (дп). Основные принципы дп. Функциональные уравнения Беллмана.

Задачи для поиска оптимальных решений в системе с многошаговой структурой.2 типа: естественный ( когда нужно определить оптимальное решение на несколько лет вперед и частичное решение на каждый из годов – задача календарного планирования) и искуственный ( когда задача очень параметрична и большое пространство решений. Разбиение на подзадачи (проще решать много раз простые, чем 1 раз сложную) – планирование развитие мощностей на предприятии.

Пример: имеется группа из н-предприятий, причем известно какую прибыль (эффективность), которую мы хотели бы иметь. Z1(T)- за Т лет, но в данный момент Z0 0 неэффективный. Построить стратегию, чтобы через Т лет был оптимальный.

Особенности:

1. Будем описывать систему, состояние которой на каждом шаге определяется вектором Хт. Дальнейшее изменение состояния зависит только от этого данного состояния Хт и не зависит от того каким образом система пришла к данному состоянию. Такого рода система-система без последствия.

2. В каждом новом состоянии система переходит под воздействие какого-либо решения, т.е. можно сказать что каждое состояние есть функция состояния предыдущего шага и решение, принимаемое на очередном шаге.

X1=f1(x0, u1), x2= f2(x1, u2)

3. Можем связать с функцией выигрыша и дохода (ЦФ) Zt=φ(Xt-1,Ut) в предыдущий момент времени и принятие решения.

4. Очевидно, что на вектор Хт могут накладываться разные ограничения определяю ОДР (G)

Требуется: Найти такую допустимую последовательность действий для каждого шага, переводящего систему из некоторого начального состояния в некоторое конечное состояние так, чтобы получить максимум или минимум значение ф-ции цели за все Н-этапов. Любая последовательность действий, переводящая систему из начального состояния Х0 в Хт называется стратегией управления. Любая допустимая стратегия управления, приносящая целевой ф-ции экстремум будет называться оптимальной.

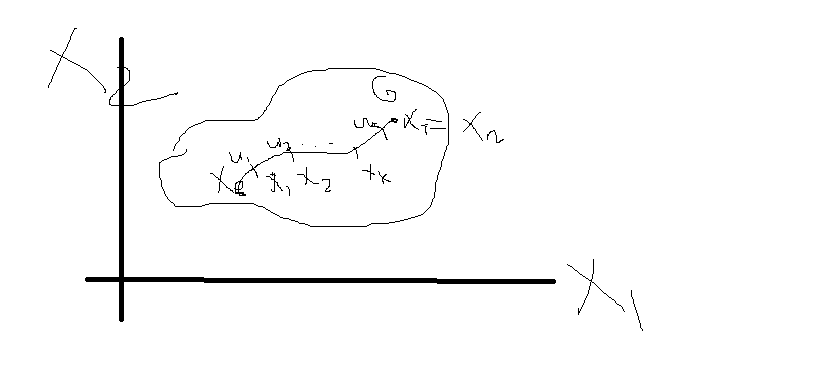
Геометрическая интерпретация:

Выбор оптимальной траектории.

Система с фазовым пространством - система, где каждая точка ОДР является некоторым состоянием.

Где Х0 и Хт известны – задача с закрепленными концами.

Где задана область – задача с незакрепленными концами( совбодная)

Принципы динамического программирования.

1. Принцип оптимальности. Оптимальная траектория перехода из некоторого начального состояния в целевое, есть сумма оптимальных траекторий движения на каждом из шагов. На систему могут накладываться ограничения которые и образуют область допустимых решений.

2. Принцип погружения. Природа задачи не меняется при изменении числа шагов по переходу системы из одного состояния в другое. Т.е. форма задачи инварианты по отношению к числу шагов Н.

Метод динамического программирования основан на применении принципа оптимальности Беллмана: каково бы ни было состояние системы перед очередным шагом, необходимо выбирать управление на этом шаге так, чтобы доход на данном шаге вместе с оптимальным доходом на всех последующих шагах был максимальным.

Из принципа оптимальности следует, что оптимальную стратегию управления можно получить, если сначала найти оптимальную стратегию управления на ом шаге, затем на двух последних шагах, затем на трёх последних шагах и т. д., вплоть до первого шага. Таким образом, решение рассматриваемой задачи динамического программирования целесообразно начинать с определения оптимального решения на последнем, ом шаге. Для того чтобы найти это решение, очевидно, нужно сделать различные предположения о том, как мог окончиться последний шаг, и с учётом этого выбрать управление обеспечивающее максимальное значение функции дохода Такое управление, выбранное при определённых предположениях о том, как окончился предыдущий шаг, называется условно оптимальным управлением.

Итак, принцип оптимальности требует находить на каждом шаге условно оптимальное управление для любого из возможных исходов предшествующего шага.

Для того чтобы построить алгоритм решения задач динамического программирования, дадим математическую формулировку принципа оптимальности Беллмана.

Пусть − максимальный доход, получаемый за шагов при переходе системы S из начального состояния в конечное состояние при реализации оптимальной стратегии управления а максимальный доход, получаемый при переходе из любого состояния в конечное состояние при оптимальной стратегии управления на оставшихся шагах. Тогда

при

Последнее выражение представляет собой математическую запись принципа оптимальности Беллмана и называется основным функциональным уравнением Беллмана. С использованием этого уравнения находится решение рассматриваемой задачи динамического программирования.