Параметры элементов для прямой и обратной последовательностей
Все сопротивления,
которыми характеризуются отдельные
элементы в нормальном симметричном
режиме, а также в симметричном переходном
процессе, по сути, являются сопротивлениями
прямой последовательности (исключение
составляет реактивность, используемая
при определении постоянной времени
).
Такими элементами можно практически
считать реакторы.
Система токов нулевой последовательности резко отличается от систем токов прямой и обратной последовательностей, вследствие чего сопротивления нулевой последовательности в общем случае весьма существенно отличаются от соответствующих сопротивлений двух других последовательностей.
Синхронные машины
Магнитный поток, созданный токами обратной последовательности синхронной частоты, вращаясь относительно ротора с двойной синхронной скоростью, встречает на своем пути непрерывно изменяющееся магнитное сопротивление. Это обусловлено магнитной не симметрией ротора и тем, что наведенные в продольных и поперечных контурах ротора токи создают различные реакции. Таким образом, поток обратной последовательности гармонически изменяется с двойной синхронной скоростью в пределах между наибольшим и наименьшим значениями.
Поток обратной последовательности синхронной частоты в общем случае вызывает в статоре нечетные гармоники, которые искажают синусоидальную форму магнитного поля статора.
Для синхронной машины без демпферных обмоток выражение реактивности имеет вид:
.
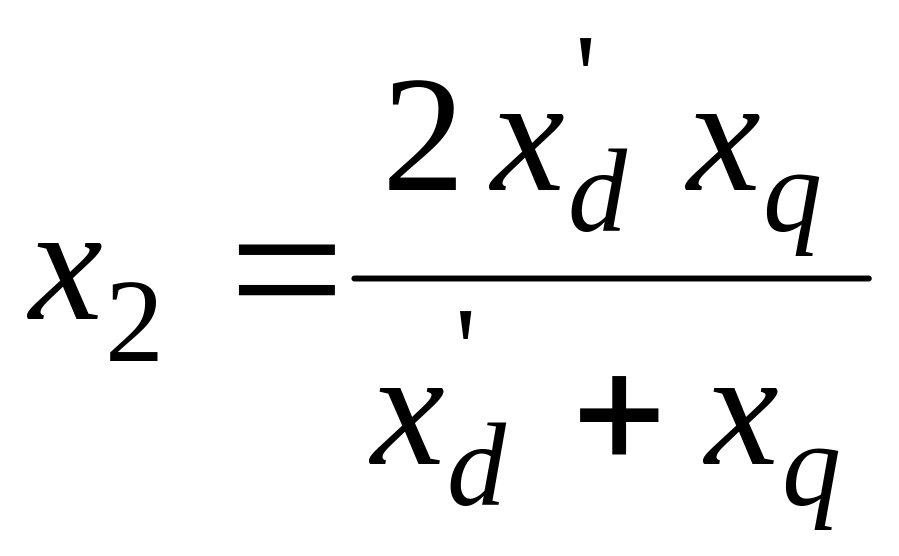(61)
Она представляет собой реактивность обратной последовательности и определяется как отношение подведенного синусоидального напряжения обратной последовательности синхронной частоты к основной гармонике тока обратной последовательности. Данная реактивность может быть представлена следующей схемой замещения (рис.28):
Рис.28. Схема замещения, определяющая реактивность синхронной машины
Представим, что
напряжение обратной последовательности
приложено не непосредственно к статору
машины, а через произвольную реактивность
.
Тогда общая реактивность обратной
последовательности всей цепи будет:
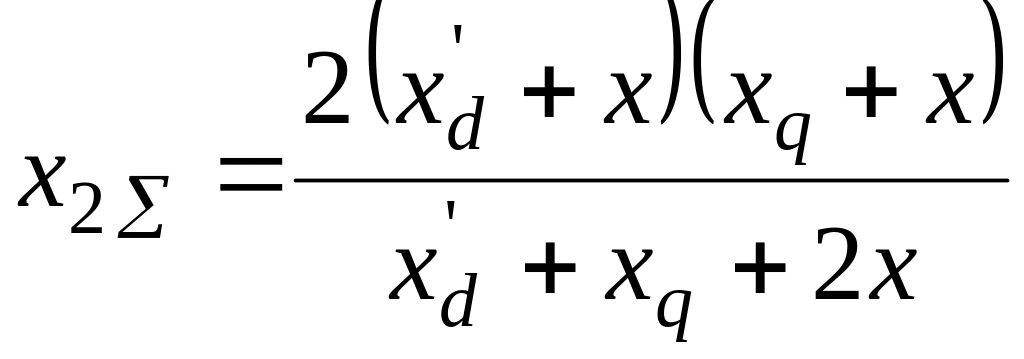(62)
и на долю самой машины приходится величина
.
(63)
Как видно из (63) реактивность зависит от внешней реактивности . С увеличением внешней реактивности реактивность обратной последовательности машины стремится в пределе к
,
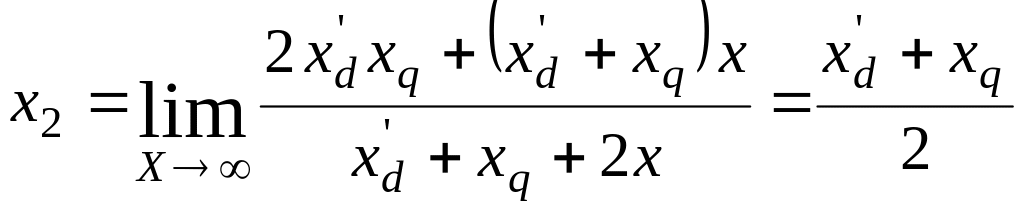(64)
что соответствует третьей гармонике тока. Для получения данной реактивности необходимо разомкнуть рубильник Р в схеме рис.28.
При несимметричном режиме машины поле обратной последовательности основной частоты вызывает в статоре весь спектр нечетных гармоник. В этом случае схема замещения рис.28 может быть развита в бесконечную цепную схему замещения, результирующая реактивность которой составляет:
.
(65)
Для машины с
демпферными обмотками реактивность
может быть определена по тем же выражениям,
если заменить в них
и
на
и
.
Величины реактивностей
и
обычно ближе друг к другу, чем
и
.
Поэтому у машин с полным демпфированием
разница в значениях
очень мала.
В практических расчетах для синхронных машин целесообразно принимать реактивность по выражению (64). Однако если необходимо учитывать высшие гармоники, то надлежит использовать более точное выражение (65).
В качестве приближенных принимают соотношения, указанные в таблице 3.
Табл.3 Соотношения реактивностей
Машины без демпферных обмоток |
|
Турбогенераторы и машины с продольно-поперечными демпферными обмотками |
|
При практических расчетах используют дополнительное упрощение и принимают для турбогенераторов и машин с продольно-поперечными демпферными обмотками
.
(66)
Токи нулевой
последовательности создают практически
только магнитные потоки рассеяния
статорной обмотки, которые меньше токов
прямой и обратной последовательности.
Поэтому величину
принимают
.
(67)