Отношения

Пусть дано множество А. Если вектор (a₁, a₂,... a_n) Î G, то говорят, что элементы, составляющие его, вступают в n – местно отношение Ф. Ф=(А,G), причем GÍАⁿ.

1. Если n=1, то отношение называется свойством.

2. Если n=2, то отношение называется бинарным.

Диагональю множества A² называется график _A={(x,x)|xA}.

Операции :

Пусть даны Ф=(А,G) и Ψ=(А,F) =>

если (x,y) G  xφy;

ФÈΨ=(A,GÈF);

не Ф=(A,A²\G);

Ф^-1=(A,G^-1);

ФΨ=(A,GF);

Ф\Ψ=(A,G\F);

ФΨ=(A,GF).

Свойства отношений:

1. Рефлексивность. _xÎА (xφx) или _A²G – все точки диагонали включены в график ;

2. Антирефлексивность _xÎА не (xφx) или _AG= -диагональ не принадлежит графику ;

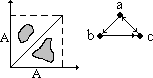3. Симметричность _xÎА"_yА(xφyyφx) или G=G^-1 – симметрично относительно диагонали ;

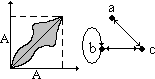4. Антисимметричность. _xÎА"_yА (xφy и yφxx=y) или _xÎА"_yА (xφy и xy  не(yx)) или GG^-1 D_A – нет точек, симметричных относительно главной диагонали:

;

5. Транзитивность _xÎА"_yА _zА(xφy и yφz xφz) или GGG

;

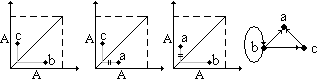6. Связность "_xÎА"_yÎА(x≠y => xφy или yφx) или A²\D_AGG^-1:

• Отношение называется частичного порядка, если выполняются свойства 1,4,5;

• Отношение называется строгого порядка, если выполняются свойства 2,4,5;

• Отношение называется строго линейного порядка, если выполняются 2,4,5,6;

• Отношение называется отношение эквивалентности, если выполняются 1,3,5.

Пример:

Пусть дано отношение xφy ↔ x тёща y:

Д оказать: утверждение «если выполняются свойства 3, 5, то выполняется 1» - ложно.

Док-во:

Пример, когда отношение на множестве А={a,b,c} обладает свойствами :

Разбиения

П усть дано множество А. Разбиением этого множества называется система непустых попарно непересекающихся множеств m={{A_i}| A_i0, ik→A_iA_k=, A_i=A}, в объединении дающих множество А. Отношение называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Теорема (о разбиении отношения эквивалентности): Каждое разбиение множества порождает на нем отношение эквивалентности.

Док–во:

Пусть имеется множество А и m. Введём отношение Ф_m=xφ_my  найдётся k : xA_k и yA_k. Тогда это отношение является отношением эквивалентности.

1. Рефлексивно: _x xφ_mx – очевидно, т.к. при разбиении x попал в один класс сам с собой;

3. Симметрично: _x,_y xφ_my→yφ_mx ;

5. Транзитивно: _x_y_z xφ_my и yφ_mz→xφ_mz – так как множества A_i и A_k не пересекаются.

ч.т.д.

Ф_m - отношение, порождённое разбиением m; оно является отношением эквивалентности.

Фактор-множество – множество классов эквивалентности.

Теорема (о порождении отношением эквивалентности разбиения множества): Каждое отношение эквивалентности, заданное на множестве A, порождает разбиение этого множества.

Пусть имеется множество А и отношение эквивалентности Ф, заданное на этом множестве.

Док-во: Пусть [a]=a/φ={x | xφa}, [b]=… Продолжаем, пока один эл­емент не попадёт в один и тот же класс. m={[a]|aA} – фактор – множество

1. a[a]  [a]0;

2. [a][b]. Пусть [a][b]0, тогда с[a] и c[b] → cφa и cφb (из симметричности cφaaφc) → aφc и сφb (из транзитивности получаем ab) → b[a] противоречие, разные классы не имеют общих элемен­тов. ч.т.д.

Индекс разбиения – мощность фактор-множества.