Самарский Государственный Аэрокосмический Университет

Лекции по математической логике

Лектор: Тишин В. В.

Напечатал: Студент СГАУ 6 факультета, гр № 622

Соловьёв Илья

Самара 2006

Теория множеств 2

Основные понятия 2

Способы задания множеств 2

Декартово произведение и векторы 3

Соответствия 4

Отношения 6

Разбиения 7

Факторизация отображения 8

Отношения порядка 8

Теория алгоритмов. 10

Понятие алгоритма. 10

Машина Тьюринга. 10

Числовая функция 10

Кодировка машин Тьюринга. 11

Алгоритмически неразрешимые проблемы. 11

Проблема применимости. 11

Нормальные алгоритмы Маркова 12

Рекурсивные функции. 13

Операция минимизации. 14

Предикаты 15

Основные понятия 15

Операции над предикатами 15

Предикатные формулы. 17

К – значные логики 18

Основные понятия 18

Функции k-значной логики. 18

Законы Моргана: 18

Формальные теории 21

Основные понятия 21

Свойства вывода из гипотез 21

Классическое исчисление высказываний 21

Теория множеств Основные понятия

Запись означает, что элемент a принадлежит множеству А. Запись означает, что b не является элементом множества А.

Если множество не содержит элементов, то оно называется пустым и обозначается символом Ø.

Примеры множеств:

N = {1, 2, 3…} – множество натуральных чисел;

N₀ = {0, 1, 2, 3…} – множество натуральных чисел и ноль;

Z = {-2, -1, 0, 1, 2…} - множество целых чисел;

Q = { - несократимая дробь, где } – множество рациональных чисел;

R – множество действительных чисел (кроме числа 0,999…, запись которого запрещена);

I – множество иррациональных чисел;

C – множество комплексных чисел;

Множество конечно, если существует такое , которое равно количеству элементов множества. Число элементов множества - мощность множества, обозначается |A|=k.

Если для любого можно найти k различных элементов из множества В, то В – бесконечное множество:

Запись означает: множество А включено во множество В, т.е. каждый элемент множества А является элементом множества В (обратное неверно). Таким образом, если . В этом случае А – подмножество, В - надмножество.

Для любого множества А выполняется: .

Теорема (о транзитивности включений):

то .

Док-во:

Для любого x, , если , то . А т.к. , то . Значит, по определению включения . ч.т.д.

Если , то - множество А строго включено во множество В. Если и , то А – собственное подмножество В.

Если и .

Пример: Пусть А={1}; B={{1},2}; C={{{1},2},3}. Тогда запись , неверна, т.е. принадлежность не обладает свойством транзитивности.

Способы задания множеств

1. Перечисление: A={a,b,c}; B={1,2,3,...,100} (повтора элементов быть не должно)

2. Порождающая процедура – алгоритм получения элементов множества из элементов другого (заранее известного) или получение элементов множества из элементов этого же множества, полученных ранее: .

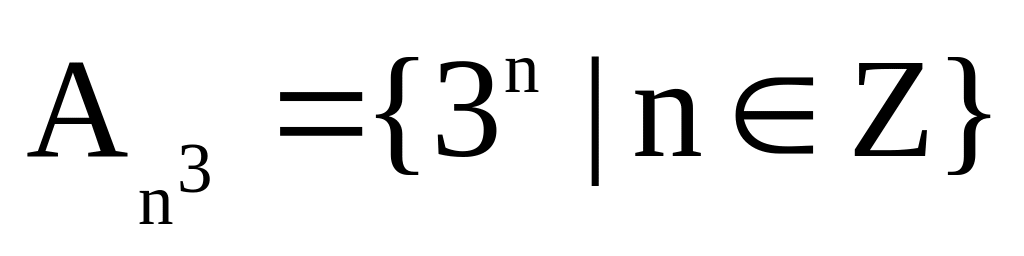3. Распознающая процедура – алгоритм который для любого элемента а определяет принадлежность его множеству А: А_е={271, 828,182,845,…} – знаки числа e.

1. АВ = {х | хÎA или хÎВ} – объединение:

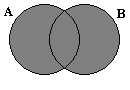
2. А∩В ={х | xÎA и хÎВ} – пересечение:

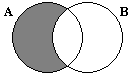
3. А\В ={x | xÎA и xÏB} – разность:

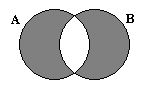
3. А Δ В=(A\B)È(B\A) – симметрическая разность:

4. Ā = {x | xU\A } – дополнение, где U – универсальное множество:

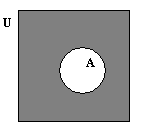
Второе определение разности: А Δ В=(AÈB) \ (A  B).

Докажем равенство: (A\B)È(B\A)=(AÈB) \ (A B).

Док-во: Пусть А={1, 2}; B={2, 3}. Тогда (AÈB)\(AB) ={1, 2, 3}\{2}={1, 3}, а (A\B)È(B\A)={1}È{3}={1, 3}. ч.т.д.

Опр: Множества А и В находятся в общем положении, если:

1. существует такое а, что аÎА, но а ÏВ;

2. существует такое b, что bÎB, но b ÏA;

3. существует такое c, что c ÎА и c ÎВ.

Теорема (о четырех возможных): для любых множеств А и В справедливо хотя бы одно из четырех возможных утверждений:

1.AÍB;

2.BÍA;

3.AB=Æ;

4.A∞B.

Док-во: Допустим, что есть пара множеств, для которых ни одно из вышеперечисленных утверждений не выполняется:

1. AB => существует такое a, что aÎA и aÏB;

2. BA => существует такое b, что bÎB и bÏA;

3. AB≠Æ => существует такое с, что сÎA и cÎB;

4. .

Т.о. получаем противоречие, т.к. из 1,2,3 следует, что A∞B. ч.т.д.

1. класс множеств (класс А): А={X | XÎX};

2. класс множеств (класс B): B={X | XÏX}.

В результате получаем парадокс:

B Î (I) => BÎB => BÏB;

B Î (II) => BÎB => BÏB.