Колебания и волны.

1 .Свободные механические и электрические колебания. Дифференциальное уравнение свободных колебаний и его решения.

Колебания — повторяющийся в той или иной степени во времени процесс. 

Колебания называются свободными, если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.

Дифференциальное уравнение свободных незатухающих колебаний:

Решение уравнения:

Гармоническими называются колебания, происходящие по законам синуса или косинуса.

 x₀ амплитуда колебаний – максимальное смещение колеблющейся величины относительно положения равновесия.

 - фаза колебаний. Показывает, какая часть колебаний завершена к данному моменту времени.

  - начальная фаза колебаний.

Математический маятник - механическая система, состоящая из материальной точки, подвешенной на невесомой нерастяжимой нити длины l.

Пружинный маятник - механическая система, состоящая из пружины жёсткостью k, один конец которой жёстко закреплён, а на втором находится груз массы m.

Электромагнитные колебания - взаимосвязанные колебания электрических (E) и магнитных (Н) полей, составляющих единое электромагнитное поле. Распространение Э. к. происходит в виде электромагнитной волны . Э. к. представляют собой дискретную совокупность фотонов, и только при очень большом числе фотонов их можно рассматривать как непрерывный процесс.

2. Колебания координаты, скорости и ускорения. Колебания энергии.

Ускорение колебаний меняется во времени по закону синуса или косинуса:

Зная уравнение колебаний скорости v(t) всегда можно найти уравнение колебаний ускорения a(t), взяв производную от функции v(t) или вторую производную от функции координаты x(t).

Отсюда максимальное ускорение (амплитуда ускорения а max) равно произведению амплитуды скорости маятника и циклической частоты (или произведению амплитуды координаты маятника и квадрата циклической частоты).

Во времени максимумы ускорения, максимум скорости и максимум координаты не совпадают:

- когда а = а max, тогда v = 0 и x = - x max (максимальное отклонение от положения равновесия);

- когда v = v max, тогда a = 0 и x = 0 (положение равновесия).

Скорость колебаний v меняется во времени по закону синуса или косинуса:

Зная уравнение колебаний x(t) всегда можно найти уравнение колебаний скорости v(t), взяв производную от функции x(t).

Отсюда максимальная скорость (амплитуда скорости v max) равна произведению амплитуды координаты маятника и циклической частоты.

Во времени максимум скорости и максимум координаты не совпадают:

- когда v = v max, тогда x = 0 (положение равновесия);

- когда x = x max, тогда v = 0 (максимальное отклонение от положения равновесия).

Энергия гармонических колебаний.

        При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W:

(Скорость тела v = ds/dt)

        Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы:

где U - потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.

        Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил (направленная к центру О сила модуль которой пропорционален расстоянию r от центра О до точки приложения силы)) мы имеем:

для кинетической и потенциальной энергии механического маятника, можно сделать следующие выводы:

1. Полная механическая энергия тела не изменяется при колебаниях 

  2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника.  3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на p (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная - минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно.

        В случае электрических колебаний энергия в конуре представляет собой сумму энергии электрического поля, запасенной между обкладками конденсатора, и энергии магнитного поля, запасенной в катушке с индуктивностью. Вычислим обе составляющие.

        Сравнивая эти формулы, можно сделать следующие выводы:

1. Полная энергия в контуре остается неизменной:

 

2. Частота колебаний энергий в 2 раза превосходит частоту колебаний заряда и тока в контуре.  3. Электрическая и магнитная энергии сдвинуты по фазе на полпериода друг относительно друга; происходит непрерывное перекачивание энергии из одной формы в другую и обратно.

        Поскольку в контуре происходят колебания электрической и магнитной энергий, электрический колебательный контур также называют электромагнитным.

3 .Сложение гармонических колебаний

        Если колебательная система одновременно участвует в двух (или более) независимых колебательных движениях, возникает задача - найти результирующее колебание. В случае однонаправленных колебаний под этим понимается нахождение уравнения результирующего колебания; в случае взаимно перпендикулярных колебаний - нахождение траектории результирующего колебания.

Метод векторных диаграмм

        Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А. Очевидно, что угол j = wt + j₀ где j₀ - начальный угол.

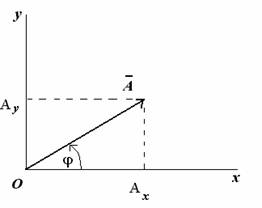
        Проекции вектора А на оси координат запишутся:

Видно, что проекции вращающегося вектора на оси координат по форме совпадают с уравнением гармонических колебаний, если угловой скорости вектора сопоставить угловую частоту колебаний, а начальному углу - начальную фазу.

        Проводя аналогию дальше, можно сказать, что результат сложения двух однонаправленных колебаний можно получить следующим путем: необходимо сложить два вектора, а проекции суммарного вектора на оси координат будут являться уравнениями результирующего колебания. Рассмотрим этот метод на примере сложения двух колебаний с произвольными частотами. Пусть наше тело участвует в двух совпадающих по направлению колебаниях:

        Сопоставим этим колебаниям два вектора А₁ и А₂, вращающихся с соответствующими угловыми скоростями.

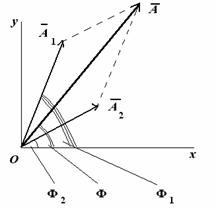
        Сопоставляем колебаниям проекции векторов на ось y. Задача сложения колебаний сводится к нахождению проекции вектора А на ось y (амплитуда результирующего колебания) и угла f(фаза результирующего колебания).

        Из очевидных геометрических соображений находим:

        Отметим, что в общем случае сложения колебаний с разными частотами амплитуда результирующего колебания будет зависеть от времени. Если же частоты одинаковы, то , то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так:

        Рассмотрим сложение двух однонаправленных колебаний с неравными, но близкими частотами, то есть , и пусть для определенности  . Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний

получим уравнение суммарного колебания:

        Полученное результирующее колебание не является гармоническим (сравним с уравнением (1)); такого вида колебания носят название биений, название понятно, если посмотреть на график колебаний.

        Величина, стоящая перед синусом, меняется со временем относительно медленно, так как разность частот мала. Эту величину условно называют амплитудой биений, а разность складываемых частот   - частотой биений (циклической).

        При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x).

например, сложим два колебания с одинаковыми частотами:

исключив время, получим:

        В общем случае это - уравнение эллипса. При A₁=A₂ - окружность, при   (m - целое) - отрезок прямой.

        Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур Лиссажу.