Загвязинский, в.И. Теория обучения. Современная интерпретация /в.И. Загвязинский. – м.: Академия, 2001. – 297 с.
.Качалко,в.Б. Поисково-исследовательская технология начального обучения математике /в.Б. Качалко.-- Мозырь: уо мгпу им. И.П. Шамякина, 2008.-149 с.
3.Загвязинский,В.И. Методология и методика дидактического исследования / В.И. Загвязинский.–М.:Высшая школа, 2002. - 136 с. Начальным этапом осуществления поис-ковой деятельности является поста-новка учебной задачи, которая отличается от конкретно–практической задачи, в кото-рой ищут способ решения, чтобы най-ти ответ на вопрос именно данной задачи, а не общий способ решения всего класса таких задач. Задача может превратиться в учебную только в том случае, если ученик самостоятельно или под руководством учи-теля осуществляет её переформулировку, чтобы найти обобщённый способ решения данного класса задач. Это становится возможным при условииях: учитель и ученики участники поиска, действия учителя разрешается учащимся критико-вать; учитель не должен грубо вмешивать-ся в поиск и навязывать ученикам правильный путь решения; учитель после решения задачи организует оценку дан-ного способа для решения задач других задач данного класса [3], [4], [5].
Однако наиболее действенной для формирования умений решать задачи, приобретая при этом осознанные ЗУНы, может быть не методика, а поисково-исследовательская технология обучения математике в начальных классах.
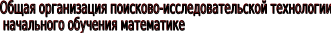
1.ВЫЯВЛЕНИЕ ОПОРНЫХ ЗУНов, ПРИЁМов И ПЛАНов ПДУ, уровней РАЗВИТИЯ с помощью ВХОДНЫХ тестов .
2.СОСТАВЛЕНИЕ СЕРИЙ ЗАДАЧ постепенно повышающейся трудности с приёмами, планами ПДУ и эвристическими подсказками, находящимися в зоне ближайшего развития учащихся .
3.СОСТАВЛЕНИЕ ТЕСТОВ (ВХОДНЫХ, ФОРМИРУЮЩИХ, ИТОГОВЫХ) ДЛЯ МОНИТОРИНГА ПОИСКА РЕШЕНИЯ ЗАДАЧ И ИССЛЕДОВАНИЯ РЕШЕНИЯ ЗАДАЧИ.
4.СОСТАВЛЕНИЕ ТЕХНОЛОГИЧЕСКОЙ МАТРИЦЫ с указанием вида задач и уровня их решения, тестов, заданий и объёма времени
5.ОРГАНИЗАЦИЯ ПОИСКА И ИССЛЕДОВАНИЯ НА УРОКАХ с мониторингом процесса поиска способов решения задач на основе тестов, а также коррекции отклонений от прогноза.
6.ВЫЯВЛЕНИЕ КОНЕЧНЫХ запрогнозированных ЗУНов, уровней РАЗВИТИЯ учащихся Сприменением итоговых тестов.
7. ОПРЕДЕЛЕНИЕ статистической достоверности результатов
Проблема мониторинга процесса обучения требует применения тестов в начальном обучении математике приобрела особую актуальность в связи со внедрением инновационных технологий, которые требуют не только чёткого планирования процесса обучения, но и выявления исходных и итоговых знаний, умений и навыков (ЗУНов), а также осуществления постоянного контроля за их усвое-нием в процессе решения учебных задач, Это значит осуществления оперативного мониторинга самостоятельного поиска решения учебных задач на разном содержании. Такие задачи в отличие от практических требуют нахождения не конкретного ответа, а общего способа решения.
Наиболее подходящими для мониторинга являются тесты, позволяющие оперативно выявлять и корректировать отклонения от запланированного уровня усвоения ЗУНов на каждом этапе и в конце процесса обучения.
Ставится задача их применять:
для выявления исходных ЗУНов перед изучением темы (входные тесты),
при формировании новых ЗУНов (формирующие тесты),
для диагностики процесса овладения ЗУНами обучаемыми (диагностические тесты)
для проверки ИТОГОВЫХ ЗУНов этого процесса (итоговые тесты).
Чёткое выделение исходных и результативных ЗУНов и тестов к ним позволяет учителю контролировать весь про-цесс обучения, т.е. осуществлять его мониторинг от начала до конца. Если к тому же предоставить каждому ученику возможность самостоятельно работать над усвоением ЗУ-Нов в зоне своего ближайшего развития, то тогда уже говорят не о методике, а о технологии обучения, которое связывают с самостоятельным решением учебных задач при минимальной эвристический помощи со стороны.
Тест - это объективное и обычно стандар-тизированное измерение, легко поддающе-еся количественной оценке, статистической обработке и сравнительному анализу. Тесты состоят из четырёх видов заданий :1) с завершением ответа, 2) с выбором ответа, 3) на устаноле-ние последовательности, 4) на соответствие.
Тестовые задания первого вида представляют собой вопрос, на который ученик должен дать краткий ответ, дополнив предложение одним-двумя недостающим сло-вами (открытые тесты), например: Квадрат - это с равными сторонами. Такие задания нетрудно составлять, но трудно оценивать.
Наиболее широкую область применения имеют тестовые задания с многими ответами:
а) с альтернативным выбором: является ли задач с конкретным ответом «купили 24 кг яблок» учебной задачей: (да, нет);
б) с верными и неверными высказываниями: подчеркни нужные слова (вопрос: Сколько однозначных чисел? а) является задачей, 2) не является задачей;
в) с выбором одного правильного из нескольких правдоподобных ответов: выбери правильный ответ: 1) любая задача состоит: 1) из условия и вопроса, 2) только из вопроса, в) только из условия.
орядочение или классификацию объектов по определённому признаку: расставь по порядку числа от наименьшего к наибольшему (5м 3дм 1см, 5 031см, 530дм 1см, 53100мм);
д) на установление соответствия между элементами двух групп объектов: запиши число сторон в треугольнике, квадрате, пятиугольнике.
Перед составлением технологической матрицы учиетель должен чётко выделить и спланировать исходные ЗУНы и входные тесты, материал разбить на небольшие разделы с указанием одного из пяти уровней усвоения, количества учебных задач (заданий) для самостоятельного поиска решения, отводимых на раздел часов и тестовых зада-ний. Например, для обучения поискук решения задач на дви-жение выявляются исходные знания и умения.
Для плодотворного поиска решающий должен ЗНАТЬ: алгоритмы выполнения арифметических действий над отвлечёнными и именованными числами, зависимости между скоростью, временем и расстоянием; отношения одновременно, навстречу друг другу, в одном направлении, в противоположных направлениях ; структурные элементы текстовой задачи: условие и вопрос, величины и их значения, отношения и зависимости, решение, проверка решения, приёмы и планы поисковой деятельности.
Поиск будет успешным при условии владении учащимися ВХОДНЫМИ УМЕНИЯМИ: решения простых задач на нахождение при постоянной третьей величине скорости по расстоянию и времени, времени по расстоянию и времени, расстояния по скорости и времени,решения простых задач с величинами скорость, время и расстояние, моделирования отрезками пройденного расстояния, стрелочками скоростей и направлений движения, флажком места встречи.
При установлении целей обучения самостоятель-ному поиску решения задач на движение учитель должен чётко спланировать, какими знаниями и умениями должны в ИТОГЕ овладеть обучаемые , . К ним относятся ИТОГОВЫЕ ЗНАНИЯ :
1)выделение из текста задачи её сюжетного содержания и величин, отношений; условия и вопроса задачи;
2)приёмы поиска решения задач на движение;
3)способы решения всех видов задач на движение.
Учащиеся должны овладеть ИТОГОВЫМИ УМЕНИЯМИ :
1)моделировать отрезками и графами все видов задач на движение;
2)составлять планы решения задачи: по действиям и составлением выражения ;
3) оформлять решение задачи: по действиям и составлением выражения;
4) проверять решение всех видов задач на движение;
5) выбирать рациональный способ решения;
6) переносить решение в знакомую ситуацию
7) переносить способ решения в незнакомую ситуацию, например, на движение по реке.
Для мониторинга поиска решения задач нужны тесты разного вида.
ВХОДНЫЕ ТЕСТЫ служат для выявления опорных, исходных знаний.
№1. Отметь правильные ответы на вопросы:
Пройденное расстояние в тексте задачи всегда обозначается наименованиями: а) километрами, б) метрами, в) сантиметрами, г) аршинами, д) парсеками.
№2.Скорость в тексте задачи обозначается наименованиями: 1) километрами в час; 2) километрами в минуту; 3) метрами в минуту; 4) милями в час.
ДИАГНОСТИЧЕСКИЕ ТЕСТЫ служат для выявления трудностей в поиске решения задач на движение. №1. Соедини стрелочкой величины с формулами для их вычисления:
А) скорость г) S=v*t,
Б) время д) v= S:t,
В) расстояние е) t = S:v.
ФОРМИРУЮЩИЕ ТЕСТЫ требуются для проверки знаний и умений обучаемых поиску решения задач на движение
№1. Соедини словосочетания и слова стрелочками.
При одновременном движении в обозначенном направлении их скорости:
А) навстречу друг другу г) вычитаются
Б) в одном направлении д) складываются
В) в противоположных направлениях
ИТОГОВЫЕ ТЕСТЫ служат для проверки знаний и умений обучаемых поиску решения задач на движение.
№1. Два всадника выехали одновременно навстречу друг другу из городов Мозырь и Наровля, расстояние между которыми 40 км. Всадники встретились через 2ч. Найди скорость 1-го всадника, если скорость второго 1 км/ч.
Перед обучением поиску решения задач на движе-ние учитель должен спланировать, какими ЗУНа-ми обучаемые владеют в НАЧАЛЕ и должны овладеть в ИТОГЕ, в виде технологической матрицы
№ Учебный материал Уровни Опорные Количество
п\п усвоения знания тестов и за-
даний
1.Арифметические действия над арифметич. действия над
именованными числами 4 отвлеч.числ. 2 8
2Понимание сущности скорости,
времени и расстояния 3 п.2 2 6
3. Выражение взаимосвязи величин
скорости, времени и расстояния в
виде словесных правил или
формул S=v*t, v= S:t, t = S:v. 4 п.3 2 6
4.Понимание сущности выражений
одновременно, навстречу друг другу, в од-
ном и противоположных направлениях 3 п.п.3,4 2 6
5.Умение решать задачи на движение
встречное. 4 п.п.1-6 2 8
6.Умение решать задачи на движение
в одном направлении. 4 п.п. 1-7 2 8
7.Умение решать задачи на движение
в противоположных направлениях 4 п.п. 1-8 2 8
Академиком В.И. Загвязинским дано определение поисково-исследо-вательской технологии обучения, под которой им понимается «разработка средств (предписаний, приёмов) для того, чтобы,
во-первых, помочь уч-ся в осознании проблемно-
сти предъявляемых задач (сделать проблемность наглядной),
во-вторых, найти способы разрешения проблемных ситуаций (заключённых в задачах), личностно-значимых для учащихся,
и, в-третьих, научить их видеть и анализировать проблемные ситуации, вычленять проблемы и задачи».
включает следующие этапы работы:
ВЫЯВЛЕНИЕ ОПОРНЫХ ЗУНов, ПРИЁМов И ПЛАНов ПДУ, уровней РАЗВИТИЯ с помощью ВХОДНЫХ тестов .
СОСТАВЛЕНИЕ И ПРИМЕНЕНИЕ СЕРИЙ ЗАДАЧ постепенно повышающейся трудности с приёмами, планами ПДУ и эвристическими подсказками, находящимися в зоне ближайшего развития учащизся .
СОСТАВЛЕНИЕ И ПРИМЕНЕНИЕ ТЕСТОВ ДЛЯ МОНИТОРИНГА ПОИСКА РЕШЕНИЯ ЗАДАЧ (ВХОДНЫХ, ФОРМИРУЮЩИХ,ДИАГНОСТИЧЕСКИХ И ИТОГОВЫХ).
СОСТАВЛЕНИЕ ТЕХНОЛОГИЧЕСКОЙ МАТРИЦЫ с указанием вида задач и приёмов ПДУ к ним тестов и объёма времени.
ОРГАНИЗАЦИЯ ПДУ НА УРОКАХ с мониторингом процесса поиска способов решения задач на основе формирующих и диагностических тестов, а также коррекции отклонений от прогноза.
ВЫЯВЛЕНИЕ КОНЕЧНЫХ запрогнозированных ЗУНов и уровней РАЗВИТИЯ с применением итоговых тестов.
ОПРЕДЕЛЕНИЕ статистической достоверности результатов.
ПОИСКОВО-ИССЛЕДОВАТЕЛЬСКАЯ ТЕХНОЛОГИЯ ОБУЧЕНИЯ ПОИСКУ РЕШЕНИЯ И ИССЛЕДОВАНИЮ РЕШЕНИЯ ЗАДАЧ НА НАХОЖДЕНИЕ ПЕРИМЕТРА И ПЛОЩАДИ ПРЯМОУГОЛЬНИКА
ПОИСК РЕШЕНИЯ ЗАДАЧИ ОБЫЧНО НАЧИНАЕТСЯ С ВЫЯВЛЕНИЯ И АКТУАЛИЗАЦИИ ОПОРНЫХ ЗНАНИЙ УМЕНИЙ УЧАЩИХСЯ ПО ТЕМЕ УРОКА
Перед решением задач на вычисление периметра и площади прямоугольника небходимо выяснить знание таблиц мер длины и площади и лучше всего в их сопоставлении. Предлагается таблицы мер записать по образцу:
1 км = 1 000 м 1 кв. км = 1 000 000 кв.м ( 1000х1000)
1 м = … дм 1 кв. м = … кв. дм
1 дм = … см 1 кв. дм = … кв см
1 см - … мм 1 кв. см - …кв.мм
Затем даются тесты на выявление опорных знаний:
Как по таблице мер длины составить таблицу мер площади?
Тест №1.Обведи кружком правильный ответ:
Увеличить единицы мер длины в 10 раз.
Увеличить единицы мер длины в 100 раз.
Увеличить единицы мер длины в 1 000 раз.
Перемножить единицы мер длины сами с собой
Выбери и обведи кружком правильную формулу вычисления
ПЕРИМЕТРА ПЛОЩАДИ прямоугольника
Р- (а+в) х 2 1) S-= ахв в
Р – ах2 + в 2) S = в : а а
Р – а + в х 2 3) S = а : в а
Р – а х 2 + в х 2 4) S = в х а
Реши задачу, используя формулы, Подставь по решению задачи
в предложенной таблице соответствующий номер задачи,
Задача № 1. Ширина дна аквариума прямоугольной формы