Тест
по курсу «Математика и информатика»
для студентов I курса
направления подготовки
034400.62 «Физическая культура для лиц с отклонениями в состоянии здоровья (адаптивная физическая культура»
профилю подготовки
«Адаптивное физическое воспитание»
Элементы аналитической геометрии на плоскости
Парабола имеет … фокусов.
Гипербола имеет … фокусов.
Эллипс имеет … фокусов.
4. Каноническое уравнение эллипса имеет вид…
5. Каноническое уравнение гиперболы имеет вид…
6. Уравнение прямой, проходящей через данную точку, имеет вид…
7.
Условие параллельности двух прямых
и
имеет вид…
8. Условие перпендикулярности двух прямых и имеет вид:
9. Уравнение прямой в отрезках имеет вид…
10. Угол между двумя прямыми и находят по формуле…
11.
Уравнение
на плоскости определяет…
12. Расстояние между точками А(5;12) и В(-7;3) равно…
13. Установите соответствие между кривой второго порядка и ее уравнением.
-
Парабола
Эллипс
Гипербола
Окружность
14. Даны точки А(2;3) и В(-6;5). Тогда координаты середины отрезка АВ равны…
15. Расстояние между точками А(1;2) и В(k;-2) равно 5 при k равном…
16. Даны точки А(-7;3) и В(3;5). Тогда сумма координат середины отрезка АВ равна…
17.
Неизвестная величина y
в записи «Точка
принадлежит линии
»
может принимать два следующих значения:
18. Уравнение окружности, изображенной на рисунке, имеет вид:
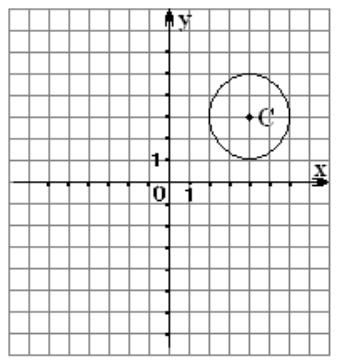
19.
Центр окружности, заданной уравнением
,
лежит в точке…
20. Даны две смежные вершины квадрата: А(3;5), В(6;9). Тогда площадь квадрата равна…
21. Точка (-2;1) лежит на прямой с уравнением…
Элементы аналитической геометрии в пространстве
1. Если два вектора
и
равны, то…
2. Как называется
уравнение прямой
?
3. Для направляющих косинусов вектора имеет место соотношение:
4. Как называется
уравнение плоскости
?
5. Какой координаты вектора в пространстве не существует?
6. Ненулевой вектор, перпендикулярный плоскости называется…
7. Если
и
,
то выражение
является условием…
8. Ненулевой вектор, параллельный прямой называется…
9. Какая операция над векторами в пространстве существует, а на плоскости нет?
10. Условие
параллельности двух плоскостей
и
имеет вид:
11. Если на векторах
и
построить
параллелограмм, то модуль их векторного
произведения
будет
равен…
12. Условие перпендикулярности двух плоскостей и имеет вид:
13. Для вектора
в выражении
,
векторы
называются….
14. Как называются
уравнения прямой
?
15. Длину вектора определяют по формуле…
16. Условие
параллельности прямой
и
плоскости
имеет
вид…
17. Косинусы углов, образуемых радиус-вектором с координатными осями OX, OY, OZ, называются направляющими…
18. Два вектора и коллинеарны тогда и только тогда, когда…
19. Два вектора и перпендикулярны тогда и только тогда, когда…
20.Условие перпендикулярности прямой и плоскости имеет вид:
21. Если плоскость
проходит через точку
,
то координата y0
равна…
22. Если точка
Р(2;3;4)
принадлежит
плоскости
, то коэффициент А
равен…
Элементы линейной алгебры
1. Матрица, состоящая
из m
строк и n
столбцов при
,
называется…
2. Если в данной матрице все строки сделать столбцами, то получится…
3. Умножать можно только… матрицы.
4. Если число столбцов m матрицы А равно числу строк m матрицы В, то две матрицы А и В называются…
5. Определитель,
получающийся из заданного путем
вычеркивания из него
-той
строки и
-того
столбца называется…
6. Число, равное
называется…..
7. Обратной для
квадратной матрицы А
называется
матрица
,
удовлетворяющая условию:
8. Если А – матрица системы линейных уравнений, а В – матрица свободных членов, то решение этой системы имеет вид:
9. Какой операции над матрицами не существует?
10.
Определитель
равен…
11.
Матрицей, которую можно сложить с
матрицей
,
может быть матрица…
12.
Заданы матрицы
и
.
Тогда решением матричного уравнения
А+Х=В
является…
13.
Дана система уравнений
.
Для того, чтобы найти значение переменной
x
при решении этой системы по формулам
Крамера, достаточно вычислить только
определители…
14. Даны матрицы А размерности 1×6 и В размерности 6×1. Произведение ВА существует и имеет размерность…
15.
Заданы матрицы
и
.
Тогда решением матричного уравнения
А+Х=В
является…
16. Дана матрица
.
Тогда сумма элементов, расположенных
на главной диагонали этой матрицы, равна
…
17. Если определитель квадратной матрицы А третьего порядка равен -3, то определитель обратной матрицы А-1 равен…
18.
Даны матрицы
и
.
Тогда матрица А-В
равна…
Дифференциальные уравнения
1. Множество всех решений дифференциального уравнения называется…
2. В общем случае каждое дифференциальное уравнение имеет… решений.
3. Общий вид дифференциального уравнения первого порядка имеет вид…
4. При решении линейных дифференциальных уравнений первого порядка вводят подстановку…
5.
Дано
дифференциальное уравнение
.
Тогда соответствующее ему характеристическое
уравнение имеет вид …
6.
Если дифференциальное уравнение имеет
вид
,
то в общем решении
произвольная постоянная С равна...
7.
Если дифференциальное уравнение имеет
вид
,
то в общем решении
произвольная постоянная С равна...
8.
Если дифференциальное уравнение имеет
вид
,
то в общем решении
произвольная постоянная С равна...