Шпоры по уравнениям математической физики
.docx© Sirleh, Nikan, }|{enek, maximkins Ф6-07
Уравнение (1) называется линейным, если F линейна относительно U, Ux, Ut.
Уравнение (1) называется линейным, если F линейна относительно Ux и Ut.
Рассмотрим оператор LU = aUx+bUt
Опр. Направление l называется характерестическим направлением оператора L в фиксированной точке (x,t) на данной ф-ии U(x,t) Опр. Гладкая кривая Г, в каждой точке которой l является касательной называется характеристикой оператора L на данной ф-ии U(x,t) Опр. Если U(x,t) является решением уравнения LU+f=0, то l и Г называются характеристическим направлением и характеристикой квазилинейного уравнения на заданном решении U(x,t)
Диф
уравнение характеристик: Теорема: 1) Решение однородного квазилинейного уравнения LU=0 сохраняется на характеристике. 2)решение неоднородного квазилинейного уравнения LU+f=0 то l и Г называются характеристическим направлением и характеристикой квазилинейного уравнения на заданном решении U(x,t)
|
Строим решение методом характеристик
1) 2)Проводим характеристику через интересующую нас точку (x,t), x0(x,t) – точка пересечения характеристики с осью x.
3)
|
|
1)Δ=a122-a11a22>0 –уравнение гиперболического типа Uξη+F(ξ,η,U,Uξ,Uη)=0 Δ<0 – уравнение эллиптического типа Uξξ+Uηη+F(ξ,η,U,Uξ,Uη)=0 Δ=0 – уравнение парболического типа Uξξ +F(ξ,η,U,Uξ,Uη)=0 или Uηη +F(ξ,η,U,Uξ,Uη)=0 Пусть Δ>0
Потребуем, чтобы α11=α22=0
Решаем квадратное уравнение относительно φx ψx.
|
|
5.Метод характеристик(распространяющихся волн) решения одномерного волнового уравнения
|
6.Решение задачи Коши для одномерного волнового уравнения. Формула Даламбера.
|
Лемма. Пусть U(x,t) –решение задачи Коши на прямой.
И пусть F(x,t), Ф(x,t),Ψ(x,t) – нечётные(чётные), тогда U(0,t)=0 (Ux(0,t)=0) Док. По формуле Даламбера:
Если, (x,t), Ф(x,t),Ψ(x,t) – нечётные
Следствие: Краевая задача на некотором промежутке с однородным граничным условием 1 и 2 рода можно свести к з. Коши на прямой, продолжив все неоднородности в уравнениях нечётно или чётно относительно концов промежутка.
|
8. Отражение волн на границе полупрямой.
U(x,t)=F(x-at)+G(x+at) – общее решение однородного волнового уравнения 1). Подставим начальные условия
2).Из граничного условия
|
|
Характеристики – нелинейная сетка новых координат. (4) |
|
|
Диф
уравнение характеристик: Теорема: 1) Решение однородного квазилинейного уравнения LU=0 сохраняется на характеристике. 2)решение неоднородного квазилинейного уравнения LU+f=0 удовлетворяет на характеристике условию dU/-f = μdτ
Док.
1)
2)
(1) |
|
|
|
|
|
|
9. Определение, непрерывность и аналитичность Г-функции. Аналитическое продолжение Г-функции с помощью соотношения Г(z+1)=zГ(z). График Г- функции. Г-функцией или Эйлеровским интегралом 2 рода называют след ф-цию:
Св-во1: Г определена и аналитична в полуплоскости ReZ>0 Св-во2:Г(z+1)=zГ(z) Доказывается через интегрирование по частям по частям.
Следствие1:
Г(z)= Следствие2:Г(n+1)=n! Г(1)=n!
Св-во3:Г
можно аналитически продолжить на
с\(о,-1,-2,…).Точки 0,-1,-2..явл простыми
полюсами и
=
|
10. Определение В-функции. Связь Г и В-функций. В-функцией иил Эйлеровским интегралом 1 рода наз след ф-цию от двух переменных:
Cв-во1:
Св-во2:
Связь Г и В ф-ций: В(x,y)=B(y,x)= 11. Функциональные свойства В и Г-функций.
1)B(x,y)=B(y,x)
=
2)B(z,1-z)=Г(z)Г(1-z)=
3)
Док-во
(3): B(z,z)=
Следствие1:
Г(n+1/2)=
Следствие2:
|
12. Уравнение гипергеометрического типа. Теорема о производных функций гипергеометрического типа. Общий вид УГТ:
Опр. Нетривиальное решение УГТ наз. Функция гиперболического типа ФГТ
Теорема.1)ФГТ
имеет непрер. Производную всюду,за
исключением может быть нулей полинома
2)Производные
|
13. Самосопряжённый вид уравнения гипергеометрического типа.
Потребуем:
(σρn)'=τnρn
|
|
14. Полиномиальные решения уравнения гипергеометрического типа. Формула Родрига. Теорема1.Для того чтобы частным решением УГТ был полином степени n, необходимо:
Док-во:Предположим , что
Теорема2.Пусть
( Тогда частным решением УГТ является полином степени n.
|
15. Достаточное условие ортогональности полиномов гипергеометрического типа. Классические ортогональные полиномы.
Пусть
Лемма.(Дост. Усл. Ортог-ти ПГТ)
Пусть
Тогда
|
16. Классификация классических ортогональных полиномов. Полиномы Якоби, Лежандра и Чебышева. Классификация Коп
Уравнение для полиномов
Весовая функция
Формула Родрига для полиномов Якоби
|
17. Классификация классических ортогональных полиномов. Полиномы Чебышева- Лагерра. Классификация Коп
Полиномы Якоби
Уравнение для полиномов
Замена
Весовая функция
C=0,
Формула Родрига
|
|
|
|
|
|
|
Ортогональность
-выполнено,
если
Частный случай
(17) |
Ортогональность
-выполнено,
если
Частные случаи
(16) |
|
|
|
18.Классификация классических ортогональных полиномов. Полиномы Эрмита Классификация Коп
Полиномы Якоби
Полиномы
Эрмита
Уравнение для полиномов
Замена
Весовая функция
Формула Родрига
Принято
|
19. Теорема о нулях классических ортогональных полиномов. Свойства чётности полиномов Якоби и полиномов Эрмита
Рассмотрим
систему КОП
с
весом
Св-во1.
Док:1)
m=0,
2)
Предположим, что
Св-во 2
Док-во:
Св-во 3 Все нули КОП простые и лежат внутри интервала ортогональности (a,b)
|
20.Интегральное представление классических ортогональных полиномов. Производящая функция для системы классических ортогональных полиномов Интегральные представление КОП
Док-во:
Опр. Φ(z,t) наз. производящей ф-й для сист. КОП
Св-во
6
Φ Док-во:
по
св-ву 5)
По
опр-ю:
|
21.Производящая функция для полиномов Лежандра. Лемма
Для
полин Леж
при
Док-во
Для
полином Леж
Φ
Φ
По
опр-ию Φ
Замена s=-2t
При
|
|
22. Рекуррентные формулы для классических ортогональных полиномов. Вывод рекуррентных формул для полиномов Лежандра 3 последних КОП связаны след. рекурент соотн-м:
где
Док-во
по
св-ву 1
|
23. Полнота системы классических ортогональных полиномов. Теорема о разложимости функции в ряд Фурье по системе КОП. Квадрат нормы полиномов Лежандра.
Свойство:
Пусть
Теорема
разложимости: Пусть f(z)
и f’(z)
– кус. Непрерывны на любом
Лемма:
Для полиномов Лежандра
Доказательство:
|
24 Определение сферических функций. Определение присоединённых ф-ий Лежандра.
Сферическими функциями называются собственные функции оператора Лапласса, удовлетворяющие условиям непрверывности(2) и периодичности(3)
|
25. Ортогональность и квадрат нормы присоединённых функций Лежандра. Решение ур-ия Лежандра:
K=0,1,2… n=k,k+1,… Теорема.Присоедин. ф-ции Лежандра орт-ны на (-1,1) при фиксир к,т.е.:
|
|
|
|
Док-во:
Требуется
док-ть ,что m=n
Рассмотрим
По
св-ву 2
Св-во 4 (Св-во четности) Полиномы Якоби при α=β и полиномы Эрмита являются честными, если n=2k нечетными если n=2k+1
Док-во:
1)
2)
(19) |
Ортогональность
-выполнено,
если
(18) |
|
|
|
|
|
|
26. Фундаментальные сферические функции и их свойства. Общее решение уравнения Лапласа в виде ряда Фурье по системе фундаментальных сферических функций. Шаровые функции. Сферич.ф-ции след вида:
Наз.ФСФ порядка n
Св-во1:ФСФ
явл собств.ф-циями оператора : Св-во2:ФСФ орт-ны на един.сфере,т.е
Св-во3:ФСФ
образуют ортогональный базис в
CL2(D,
D={
|
27. Уравнение Бесселя. Поиск решения уравнения Бесселя в виде обобщённого степенного ряда. Функция Бесселя.
Опр. Всевозможные решения уравнения Бесселя называются цилиндрическими функциями. Ищем решение ур. Бесселя в виде обобщённого степенного ряда:
|
Билет 28. Сходимость степенного ряда для ф-ии Бесселя. Линейная зависимость функций Бесселя.
Ищем решения ввиде степенного ряда:
|
29.
Функция Бесселя порядка
Аналогично
при -
Замена
Замечание:
При
|
|
32. Функции Неймана и Ханкеля. Функ. соотношения цил. Функ.
Найдём цилиндрическую функцию, которая имеет другое асимптотическое представление
При целом ν:
При
целом
При
|
31. Асимптотические представления цилиндрических функций в окрестности точки нуль. Графики функций Бесселя и Неймана.
При
По
формуле дополнения:
Если
При
|
32. Модифицированные цилиндрические функции (цил. ф-ии мнимого аргумента). Асимптотические представления и графики.
Сделаем
замену
При
|
|
|
Теорема.
Любое вещественное решение уравнения
Бесселя при
Где
Лемма.
|
Теорема.
Для любого R>0
ст.ряд
Док-во:
Пусть
Теорема.
Ф-ии Бесселя при нецелом
|
|
R=
(26) |
|
|
|
|
|



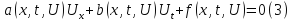

































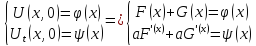
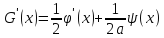
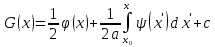







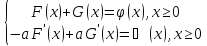
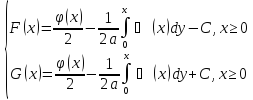









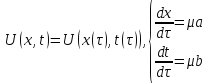


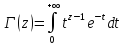
 ,n>N
,n>N =res
=res


 определена и аналитична на обл.
Rex>0,Rey>0
определена и аналитична на обл.
Rex>0,Rey>0
 –формула связи
–формула связи

 симметрии =2
симметрии =2 =2
=2

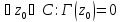





 сами
являются ФГТ и удовл.уравнению
сами
являются ФГТ и удовл.уравнению
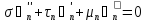
 ,
,









 )-весовая
функция
)-весовая
функция




 )
)

 ч.т.д.
ч.т.д.





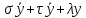 =0
=0 полиномы
Эрмита
полиномы
Эрмита полиномы
Чебышева-Лагерра
полиномы
Чебышева-Лагерра (
(
 x=az+b
Полиномы
Якоби
x=az+b
Полиномы
Якоби




 y=0
y=0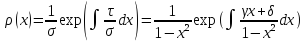



 ;
; ,
,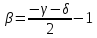


 Принято
Принято

 =0
=0 полиномы
Эрмита
полиномы
Эрмита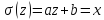 полиномы
Чебышева-Лагерра
полиномы
Чебышева-Лагерра (
(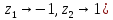
 x=az+b
x=az+b







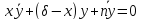

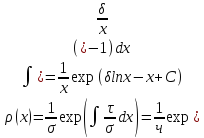

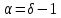 ,
,


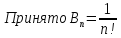
 =0-дост.усл.орт-ти
=0-дост.усл.орт-ти =0,
=0,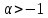

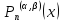 -ортог
на(0,
-ортог
на(0, )
с весом
)
с весом
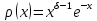
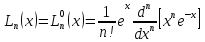 -полином
Лагерра(
-полином
Лагерра( )
)

 =0
=0 =0,
=0,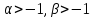

 -ортог
на(-1,1) с весом
-ортог
на(-1,1) с весом




 =
= пол .Лежандра
пол .Лежандра

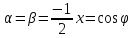

 -
-

 =0
=0 полиномы
Эрмита
полиномы
Эрмита полиномы
Чебышева-Лагерра
полиномы
Чебышева-Лагерра (
(
 x=az+b
x=az+b )
)




 y=0
/ *
y=0
/ *


 ,
,
 y=0
y=0 ,
,

 ,
C=0
,
C=0




 ,орт-к
по(a,b)
,орт-к
по(a,b) (
( )
)

 ,
,





 ;
;
 ч.т.д
ч.т.д




 ,
где простой контур С ориентирован
протии часовой ,охватывает точку z
и лежит в односвязной обл-ти
,
где простой контур С ориентирован
протии часовой ,охватывает точку z
и лежит в односвязной обл-ти
 аналитическая
ф-ия .
аналитическая
ф-ия . -
ф-ла Родрига
-
ф-ла Родрига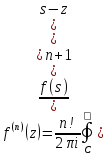 -обобщ.ф-ла
Коши для
-обобщ.ф-ла
Коши для
 аналитична в односвязной обл D
аналитична в односвязной обл D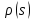 -аналитична
в D
-аналитична
в D
 -
аналитична в D
-
аналитична в D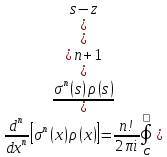 ч.т.д
ч.т.д ,
если
,
если

 в
круге
в
круге
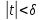
 ,
где С-тот же что и в св-ве 5
,
где С-тот же что и в св-ве 5

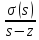 непер.
на С→огр. на С→
непер.
на С→огр. на С→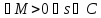


 M<1
M<1 -сход
равном в круге
-сход
равном в круге
 ч.т.д
ч.т.д






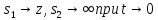


 =
= =
=





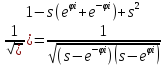


 ,
,

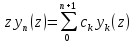
 ;
;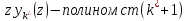
 −ву
2
−ву
2



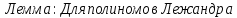


 /
/






 ч.т.д.
ч.т.д. – сходится. Тогда
– сходится. Тогда













 не огр на отр.[-1,1]
не огр на отр.[-1,1]
 решение нашего
ур-ия
решение нашего
ур-ия


 .
Предположим обратное: m<n
.
Предположим обратное: m<n ,
если m>0
,
если m>0

 не
меняет знак на
(a,b)
не
меняет знак на
(a,b) противоречие
противоречие
 m=n
m=n





 =0
=0 =0,
=0,
 ортог
на(-
ортог
на(- ,+
,+ )
с весом
)
с весом


 отвечающие с.з.
отвечающие с.з.



 )
)



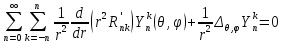




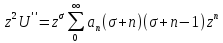
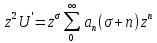




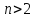



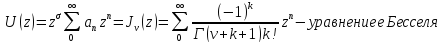
 – ур-ие
Бесселя
– ур-ие
Бесселя
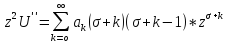




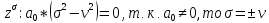


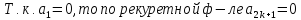
 .
Асимптотическое представление целых
ф-ии при
.
Асимптотическое представление целых
ф-ии при
 .
.

 :
:

 – ур-ие
Бесселя – разделим на
– ур-ие
Бесселя – разделим на





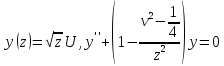
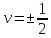 или
или
 получаем
получаем


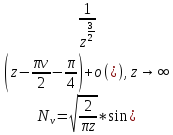
 -
общее решение уравнения Бесселя
-
общее решение уравнения Бесселя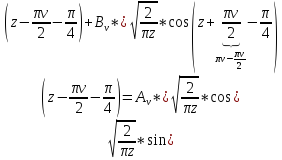


 – функция
Неймана
– функция
Неймана ,
,

 –л.н.з.,
т.к. имеют л.н.з. асимптотические
представления при
–л.н.з.,
т.к. имеют л.н.з. асимптотические
представления при

 – функции
Ханкеля 1-ого (2-ого) рода
– функции
Ханкеля 1-ого (2-ого) рода ,
,
 =
=
 ,
,


 ,
,
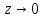 ,
,


 ,
,
 ,
,

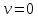 ,
то
,
то
 =
=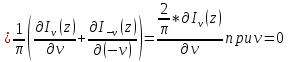
 ,
,
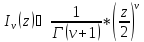




 – ур-ие
Бесселя
– ур-ие
Бесселя – общее
решение уравнения Бесселя
– общее
решение уравнения Бесселя ,
тогда
,
тогда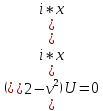
 – модифированное
уравнение Бесселя
– модифированное
уравнение Бесселя
 – функция
Бесселя мнимого аргумента
– функция
Бесселя мнимого аргумента – Функция
Макдональда
– Функция
Макдональда – монотонно
возрастает на (0;+∞)
при
– монотонно
возрастает на (0;+∞)
при
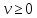

 ,
,



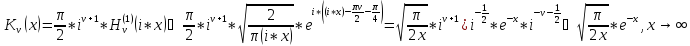
 имеет асимптотическое представление
вида:
имеет асимптотическое представление
вида:

 :
:





 сходится равномерно по z и
сходится равномерно по z и
 в замкнутой области
в замкнутой области



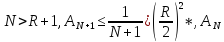 =C
=C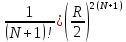
 =C
=C

 :
: