5. Критерии и количественные характеристики надежности. Понятие критериев надежности, характеристик надежности. Критерии надежности восстанавливаемых изделий.

Критерием надежности называется признак, по которому можно количественно оценить надежность различных устройств. К числу наиболее широко применяемых критериев надежности относятся: - вероятность безотказной работы в течение определенного времени P(t); - средняя наработка до первого отказа T_ср; - наработка на отказ t_ср; - частота отказов f(t) или a(t); - интенсивность отказов l(t); - параметр потока отказов w(t); - функция готовности K_г(t); - коэффициент готовности K_г. Характеристикой надежности следует называть количественное значение критерия надежности конкретного устройства. Выбор количественных характеристик надежности зависит от вида объекта.

Пусть в работе находится N элементов и пусть отказавшие элементы немедленно заменяются исправными (новыми или отремонтированными). Если не учитывать времени, потребного на восстановление системы, то количественными характеристиками надежности могут быть параметр потока отказов w(t) и наработка на отказ t_ср.

6. Показатели надежности сложных объектов. Понятие сложного объекта. Типы соединения элементов сложных объектов. Поведение сложных объектов с последовательным и параллельным соединением элементов при сбоях и отказах.

Сложные системы состоят из более простых объектов (элементов). В зависимости от характера влияния надежности элементов на надежность системы в целом различают два типа соединений элементов – основное (последовательное) и параллельное. Под последовательным соединением, с точки зрения надежности, понимают такое, при котором отказ любого элемента приводит к отказу системы в целом. Под параллельным соединением понимают такое, при котором отказ системы наступает только при отказе всех ее элементов (отказ не наступает, если работоспособен хотя бы один элемент).

ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ЭЛЕМЕНТОВ. Пусть система состоит из n элементов, каждый из которых имеет определенные характеристики надежности Pi(t), Qi(t), .i(t), t i (средняя наработка до отказа).

Если аналогичные показатели надежности системы обозначить соответственно через P(t), Q(t), .(t) и t , то можно получить следующие расчетные зависимости:

1. Из определения последовательного соединения элементов следует, что вероятность безотказной работы:

(1.15)

2. Вероятность отказа системы равна:

(1.16)

3. Интенсивность отказов системы найдем из соотношения:

откуда:

(1.17) В случае постоянной интенсивности отказов [.(t)=.=const]:

откуда:

(1.18) Если разложить функцию P(t) в ряд и учесть только два первых члена

разложения, получим:

(1.19)

4. Средняя наработка системы до отказа (.=const):

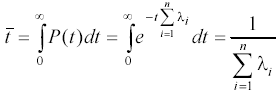(1.20)

ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ЭЛЕМЕНТОВ. 1. Из определения параллельного соединения элементов вероятность отказа системы равна:

(1.21)

2. Вероятность безотказной работы системы:

(1.22)

Пример 1.3. Система состоит из n параллельно соединенных равнонадежных подсистем, вероятность безотказной работы каждой из которых Определить потребную кратность резервирования, чтобы вероятность безотказной работы системы была не ниже

Решение:

При параллельном соединении элементов

Дальнейшее совершенствование показателей надежности современных сложных систем продолжает оставаться актуальной задачей. Важнейшими направлениями совершенствования являются внедрения показателей надежности, учитывающих индивидуальную надежность конкретных объектов; показателей надежности, учитывающих влияние надежности на эфф-ть, влияние программного обеспечения, человеческого фактора, живучести и достоверности.