Постулаты Бора:

Существуют стационарные состояния атома, находясь в которых он не излучает энергию. Для таких состояний электрон в атоме, двигаясь по круговой орбите, должен иметь квантованные значения момента импульса, удовлетворяющие условию : где m0 – масса электрона, V – скорость его движения на орбите радиуса r,  - постоянная Планка.

При переходе атома из стационарного состояния с номером n в стационарное состояние с номером m испускается или поглощается один фотон с энергией :

где Еn и Еm – энергия электрона на соответствующих орбитах

Атом может находиться только в особенных стационарных, или квантовых, состояниях, каждому из которых отвечает определенная энергия. В стационарном состоянии атом не излучает электромагнитных волн.

Электрон в атоме, не теряя энергии, двигается по определённым дискретным круговым орбитам, для которых момент импульса квантуется: , где n — натуральные числа, а — постоянная Планка. Пребывание электрона на орбите определяет энергию этих стационарных состояний.

При переходе электрона с орбиты (энергетический уровень) на орбиту излучается или поглощается квант энергии , где — энергетические уровни, между которыми осуществляется переход. При переходе с верхнего уровня на нижний энергия излучается, при переходе с нижнего на верхний — поглощается.

ФРАНКА - ГЕРЦА ОПЫТ - опыт, показавший, что внутр. энергия атома не может изменяться непрерывно, а принимает определённые дискретные значения (квантуется). Впервые поставлен в 1913 нем. физиками Дж. Франком (J. Franck) и Г. Герцем (G. Hertz). Сыграл важную роль в эксперим. подтверждении теории атома Бора (см. Атомная физика).

В опыте исследовалась зависимость силы тока I от ускоряющего потенциала V между катодом К (рис. 1) и сеткой C1; между сеткой С2 и анодом А приложен замедляющий потенциал. Электроны, ускоренные в области I, испытывают в области II соударения с атомами паров ртути, заполняющими трубку Л. На анод А попадают только те электроны, энергия к-рых после соударения с атомом достаточна для преодоления замедляющего потенциала в области III. При увеличении ускоряющего потенциала от 0 до 4,9 В гальванометр показал монотонный рост I; т.о., в этой области V соударения электронов с атомами носят упругий характер, внутр. энергия атомов не меняется. При значении V>=4,9 B (и кратных ему значениях V>=9,8; 14,7 B,...)на кривой I(V)появляются спады (рис. 2): соударения электронов с атомами становятся неупругими- внутр. энергия атомов растёт за счёт энергии электронов.

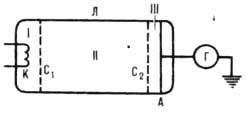
Рис. 1. Схема опыта Франка-Герца.

Таким образом, Ф.- Г. о. показал, что спектр поглощаемой атомом энергии не непрерывен, а дискретен, мин. порция энергии (квант энергии), к-рую может поглотить атом Hg, равна 4,9 эВ. Значение длины волны l=253,7 нм свечения паров Hg, возникавшее при V>=4,9 B, оказалось в соответствии со вторым постулатом Бора

где -энергии основного и возбуждённого уровней энергии; в Ф.- Г. о.

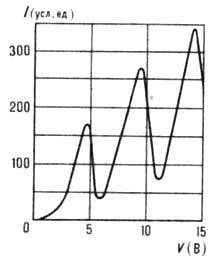
Рис. 2. Зависимость I(V), полученная в опыте Франка-Герца.

Боровская модель атома водорода — промежуточная (между классической физикой и квантовой физикой) модель простейшего атома, предложенная Нильсом Бором для объяснения наблюдаемых свойств атомов водорода. В ней объединены классические представления о взаимодействии заряженных частиц, и постулируется наличие некоторых квантовых свойств атома.

В этой модели предполагается, что точечная частица — электрон — движется вокруг точечного положительно заряженного ядра по траектории в форме эллипса и при этом не излучает электромагнитных волн. Постулируется, что только некоторые возможные орбиты движения являются разрешенными. Для таких орбит момент количества движения атома имеет вполне определенные значения, кратные кванту действия — постоянной Планка. Переход электрона с одной разрешенной орбиты на другую происходит с поглощением или потерей энергии атомом в виде порции электромагнитной энергии — кванта света.

В этой модели у атома водорода существует орбита электрона, для которой суммарная энергия (потенциальная и кинетическая) атома является самой низкой. С этой орбиты электрону можно переходить только на более «энергичные» орбиты. Находиться на этой самой «низкоэнергичной» орбите электрон может неограниченно долго.

Эта модель объясняет основные особенности спектров излучения и поглощения атомарного водорода: наличие спектральных линий и группировку их в серии.

Уравнение движения электрона имеет вид

заряд-Ze

внутренней энергии атома:

2

Волновые свойства частиц. Гипотеза де Бройля

 де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами.

Согласно де Бройлю, с каждым микрообъектом связаны, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой стороны, волновые характеристики – частота n и длина волны l.

Корпускулярные и волновые характеристики микрообъектов связаны такими же количественными соотношениями, как и у фотона:

Гипотеза де Бройля постулировала эти соотношения для всех микрочастиц, в том числе и для таких, которые обладают массой m. Любой частице, обладающей импульсом, сопоставлялся волновой процесс с длиной волны n = h / p.

На первом удачном эксперименте было обнаружено, что пучок электронов, рассеивающийся на кристалле никеля, дает отчетливую дифракционную картину, подобную той, которая возникает при рассеянии на кристалле коротковолнового рентгеновского излучения.

Впоследствии дифракционные явления были обнаружены также для нейтронов, протонов, атомных и молекулярных пучков. своих экспериментах Томсон наблюдал дифракционную картину, возникающую при прохождении пучка электронов через тонкую поликристаллическую фольгу из золота. Упрощенная схема опытов Дж. Томсона по дифракции электронов. K – накаливаемый катод, A – анод, Ф – фольга из золота.

Волновые свойства частиц

Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость

Во́лны де Бро́йля — волны, связанные с любыми микрочастицами и отражающие их волновую природу.

Модель демонстрирует мысленный эксперимент по прохождению пучка электронов через узкую щель. Подлетая к экрану с щелью, частицы взаимодействуют с ней как волны де Бройля. Поведение частиц в пространстве между экраном с щелью и фотопластинкой описывается с помощью Ψ-функции. Квадрат модуля пси-функции определяет вероятность обнаружения частицы в том или ином месте. Таким образом, попадание частиц в различные точки фотопластинки является вероятностным процессом. Если бы частицы двигались вдоль определенных траекторий, то на фотопластинке частицы регистрировались бы только напротив щели (геометрическое изображение щели), но в действительности на пластинке наблюдается интерференционная картина (экспериментальное распределение). Можно изменять в некоторых пределах ширину щели и наблюдать дифракционное размытие электронного пучка на фотопластинке. Чтобы пучок стал хорошо виден, необходимо после нажатия кнопки "Запуск" подождать некоторое время.

ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ 1927, физический закон, который утверждает, что нельзя одновременно точно измерить координаты и импульс микроскопического объекта, т.к. процесс измерения нарушает равновесие системы. Произведение этих двух неопределенностей всегда больше ПОСТОЯННОЙ ПЛАНКА. Этот принцип был впервые сформулирован Вернером Гейзенбергом.

где x, p,E, t - неопределенности (погрешности) измерения координаты, импульса, энергии и времени, соответственно; h - постоянная Планка.

Принцип неопределенности. Экспериментальные исследования свойств микрочастиц (атомов, электронов, ядер, фотонов и др.) показали, что точность определения их динамических переменных (координат, кинетической энергии, импульсов и т.п.) ограничена и регулируется открытым в 1927 г. В. Гейзенбергом принципом неопределенности. Согласно этому принципу динамические переменные, характеризующие систему, могут быть разделены на две (взаимно дополнительные) группы:

1) временные и пространственные координаты (t и q);

2) импульсы и энергия (p и E).

При этом невозможно определить одновременно переменные из разных групп с любой желаемой степенью точности (например, координаты и импульсы, время и энергию). Это связано не с ограниченной разрешающей способностью приборов и техники эксперимента, а отражает фундаментальный закон природы. Его математическая формулировка дается соотношениями:

Обычно достаточно точно указывают значение энергии микрочастицы, так как эта величина сравнительно легко определяется экспериментально.

Укажем примеры полных наборов(наборы одновреено измеримых величин),используемых для задания состояний, например, электрона и фотона. Каждый изнаборов включает четыре величины (в связи с этим говорят, что микрообъект имеетчетыре степени свободы). Для описания состояний электрона используютследующие наборы:

x, y, z, σ,

Δpx, Δpy, Δpz,σ,

E, l, m, σ

(напомним, что l,m, σ – соответственно орбитальное, магнитное испиновое квантовые числа). Подчеркнем, что координаты и составляющие импульсамикрообъекта (в данном случае электрона) попадают в разные полные наборывеличин; указанные физические величины одновременно неизмеримы. Именно поэтомуклассические соотношения E = p2/2m + U(r), M = (r . p) не работают припереходе к микрообъектам; ведь в каждое из этих соотношений входит икоордината, и импульс.

3

Волновая функция

Состояние частицы в классической механике задаётся радиус-вектором и импульсом. Что означает задать состояние? Это означает на столько охарактеризовать объект, чтобы дальше соответствующий раздел науки мог предсказать, как этот объект будет развиваться. Понятно, что смысл этих слов в различных разделах физики различен. Вот, мы недавно электричество рассматривали, что значит дать исчерпывающее описание объекта с точки зрения электричества? Надо дать распределение плотности заряда и плотности тока. Что значит задать состояние объекта с точки зрения теоретической механики? Это значит задать распределение масс, то есть плотность обычную, и напряжения. В квантовой механике мы не можем задать вот эти переменные.

Состояние частицы в квантовой механике задаётся волновой функцией , то есть функцией координат и времени, заданной в каждой точке пространства, это комплексная функция. Значит, что вы должны уловить: в классической механике мы задаём координаты и импульс частицы, в квантовой механике этого сделать нельзя, а вот когда мы хотим охарактеризовать состояние частицы, мы должны задать вот такую функцию.

Волновая функция содержит исчерпывающую информацию о состоянии частицы, то есть она позволяет дать ответы на все разумные вопросы относительно характеристик частицы. Слово «разумные» я употребил тут не ради красного словца, а со смыслом. Дело в том, что те вопросы, которые в рамках классической механике выглядят и являются разумными, не являются разумными в квантовой механике. Ну, сейчас проиллюстрируем это дело. Волновая функция имеет такой смысл: это прежде всего комплексная функция, и - это есть вероятность того, что частица будет обнаружена в окрестности точки , в элементе объёма . Первое важное обстоятельство: предсказания в квантовой механике носят принципиально вероятностный характер, это означает, что законы природы на фундаментальном уровне носят вероятностный характер.

Это надо прокомментировать. Скажем, вопрос, где находится частица, является неразумным, на него не может быть дан ответ, потому что само понятие частица находится в какой-то точке оказывается лишённым смысла. Вот, молекулы воздуха тут летают, тоже вводится вероятностное описание (просто мы не можем уследить за каждой из этих молекул), мы знаем, что она где-то есть, но мы не знаем где она. Поставим ящик, мы можем рассчитать вероятность того, что она находится в ящике. Там вероятность это мера нашего незнания, в квантовой механике эта вероятность чисто реальная: пока мы частицу не обнаружили, она потенциально находится всюду, не то, что она где-то есть, а мы не знаем где, само представление, что она где-то есть, лишено смысла. Она потенциально находится всюду, где волновая функция отлична от нуля. А когда мы локализуем это (экран поставили, там электроны обнаруживаются), вот только в этом акте измерения это потенциальное нахождение всюду оно актуализируется. Есть разница в представлениях, что она где-то есть и мы не знаем где, и тем, что она потенциально всюду, пока мы её не поймали в этой точке. Ещё раз повторю, все фундаментальные законы носят вероятностный характер.

В прошлый раз мы остановились на обсуждении волновой функции и на такой формуле: . Ещё раз повторю, что вот эта вещь (короче можно записать в таком виде| ) это вероятность того, что частица будет обнаружена в элементе объёма dV в окрестности точки . Волновая функция задана на всём пространстве, и вероятность обнаружения частицы в разных точках различна. Я уже говорил, ещё раз повторю, что в квантовой теории предсказания носят принципиально вероятностный характер, это связано не с тем, что частица по теории вероятности обнаружится, а с тем, что частица где-то есть, а мы не знаем где. Ситуация более драматичная: частица потенциально есть всюду, где , и потом где-то она обнаруживается (что-то такое происходит, где-то там частица провзаимодействовала с чем-то).1)

Если волновая функция частицы известна, то, очевидно, известно всё, что можно знать. Волновая функция исчерпывающе описывает состояние частицы, то есть может дать ответы на все разумные вопросы. Нюанс только в том, что вопросы, которые в рамках классической физики разумны, например, вопрос, где находится частица, разумный, он здесь оказывается неразумным, и ответ на него дать нельзя. Какие вопросы разумны, какие нет, мы дальше увидим по ходу дела, но в квантовой механике обнаружилось, что не на всякий вопрос, сформулированный на обыденном языке, может быть дан ответ.2) Нашей задачей будет научиться давать ответы на разумные вопросы. А пока двигаемся дальше.

Наличие в окружающем нас мире «противоестественных» (с классической точки зрения) состояний, объективность их существования подтверждены физическими экспериментами, и этот факт является прямым следствием одного из самых фундаментальных принципов квантовой механики — принципа суперпозиции состояний. Или лучше сказать наоборот: это неотъемлемое свойство природы нашло свое отражение в основном теоретическом принципе квантовой механики. Сформулировать его можно следующим образом.

Принцип суперпозиции состояний: если система может находиться в различных состояниях, то она способна находиться в состояниях, которые получаются в результате одновременного «наложения» друг на друга двух или более состояний из этого набора.

СУПЕРПОЗИЦИИ СОСТОЯНИЙ ПРИНЦИП -важнейший постулат квантовой механики, лежащий в основе её физ. содержания и матем. аппарата. Необходимость С. с. п. обусловлена корпускулярно-волновым дуализмом - всеобщим и универсальным свойством природы. С. с. п. позволяет устранить противоречие между волновым и корпускулярным описанием явлений (существовавшим в рамках классич. представлений о частицах как материальных точках, движущихся по определ. траекториям) и описать волновые явления в терминах корпускулярных представлений. Согласно С. с. п., линейная суперпозиция любых возможных состояний системы, взятых с произвольными (комплексными) коэф., является также возможным состоянием системы (подробнее см. в ст. Квантовая механика).

Уравне́ние Шрёдингера — уравнение, описывающее изменение в пространстве (в общем случае, в конфигурационном пространстве) и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах/ Его можно назвать уравнением движения квантовой частицы

где - оператор Гамильтона - аналог классической функции Гамильтона, в которой p и r заменены на операторы импульса p и координаты x .

4

Свободная частица — частица, движущаяся в отсутствие внешних полей. Так как на свободную частицу (пусть она движется вдоль оси х) силы не действуют, то потенциальная энергия частицы U(x) = const и ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией. В таком случае уравнение Шредингера (217.5) для стационарных состояний примет вид

(219.1)

Прямой подстановкой можно убедиться в том, что частным решением уравнения (219.1) является функция y(х) = Аеikx , где А = const и k = const, с собственным значением энергии

(219.2)

Функция представляет собой только координатную часть волновой функции Y(x, t). Поэтому зависящая от времени волновая функция, согласно (217.4),

(219.3)

(здесь и ). Функция (219.3) представляет собой плоскую монохроматическую волну де Бройля (см. (217.2)).

Из выражения (219.2) следует, что зависимость энергии от импульса

оказывается обычной для нерелятивистских частиц. Следовательно, энергия свободной частицы может принимать любые значения (так как волновое число k может принимать любые положительные значения), т. е. ее энергетический спектр является непрерывным.

Таким образом, свободная квантовая частица описывается плоской монохроматической волной де Бройля. Этому соответствует не зависящая от времени плотность вероятности обнаружения частицы в данной точке пространства

т. е. все положения свободной частицы в пространстве являются равновероятными.

Гармонический осциллятор в квантовой механике представляет собой квантовый аналог простого гармонического осциллятора, при этом рассматривают не силы, действующие на частицу, а гамильтониан, то есть полную энергию гармонического осциллятора, причём потенциальная энергия предполагается квадратично зависящей от координат. Учёт следующих слагаемых в разложении потенциальной энергии по координате ведёт к понятию ангармонического осциллятора.

5

Атом водорода в квантовой механике

Уравнением движения микрочастицы в различных силовых полях является волновое уравнение Шредингера.

Для стационарных состояний уравнение Шредингера будет таким:

, m – масса частицы, h – постоянная Планка, E – полная энергия, U – потенциальная энергия.

Уравнение Шредингера является дифференциальным уравнением второго порядка и имеет решение, которое указывает на то, что в атоме водорода полная энергия должна иметь дискретный характер:

E1, E2, E3…

Эта энергия находится на соответствующих уровнях n =1,2,3,…по формуле:

Самый нижний уровень E соответствует минимальной возможной энергии. Этот уровень называют основным, все остальные – возбужденными.

По мере роста главного квантового числа n энергетические уровни располагаются теснее, полная энергия уменьшается, и при n =E>0 электрон становится свободным, несвязанным с конкретным ядром, а атом – ионизированным.

Полное описание состояния электрона в атоме, помимо энергии, связано с четырьмя характеристиками, которые называются квантовыми числами. К ним относятся: главное квантовое число п, орбитальное квантовое число l, магнитное квантовое число m1, магнитное спиновое квантовое число ms.

трона в пространстве, то есть волновая функция в пространстве характеризуется тремя системами. Каждая из них имеет свои квантовые числа: п, l, ml.

Каждой микрочастице, в том числе и электрону, также свойственно собственное внутреннее сложное движение. Это движение может характеризоваться четвертым квантовым числом ms. Поговорим об этом подробнее.

A. Главное квантовое число п, согласно формуле, определяет энергетические уровни электрона в атоме и может принимать значения п = 1, 2, 3…

Б. Орбитальное квантовое число /. Из решения уравнения Шредингера следует, что момент импульса электрона (его механический орбитальный момент) квантуется, то есть принимает дискретные значения, определяемые формулой

где Ll – момент импульса электрона на орбите, l – орбитальное квантовое число, которое при заданном п принимает значение i = 0, 1, 2… (n – 1) и определяет момент импульса электрона в атоме.

B. Магнитное квантовое число ml. Из решения уравнения Шредингера следует также, что вектор Ll (момент импульса электрона) ориентируется в пространстве под влиянием внешнего магнитного поля. При этом вектор развернется так, что его проекция на направление внешнего магнитного поля будет

Llz = hml

где ml называется магнитным квантовым числом, которое может принимать значения ml = 0, ±1, ±2,±1, то есть всего (2l + 1) значений.

Учитывая сказанное, можно сделать заключение о том, что атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях (n – одно и то же, а l и ml– разные).

При движении электрона в атоме электрон заметно проявляет волновые свойства. Поэтому квантовая электроника вообще отказывается от классических представлений об электронных орбитах. Речь идет об определении вероятного места нахождения электрона на орбите, то есть местонахождение электрона может быть представлено условным «облаком». Электрон при своем движении как бы «размазан» по всему объему этого «облака». Квантовые числа n и l характеризуют размер и форму электронного «облака», а квантовое число ml– ориентацию этого «облака» в пространстве.

Резкая серия(буква s является начальной буквой наименования серии: sharp — резкий).

Главная серия:(principal — главный),

Диффузная серия:(diffuse — диффузный).

Основная серия (серия Бергмана)(fundamental — основной).:

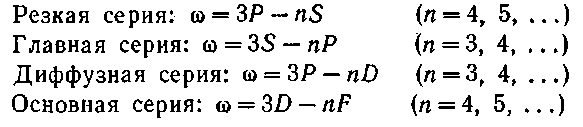
СПИНОВОЕ КВАНТОВОЕ ЧИСЛО - квантовое число, определяющее величину спина квантовой системы (атома, иона, атомного ядра, молекулы), т. е. её собств. (внутр.) момента кол-ва движения (момента импульса). Спиновый момент импульса s квантуется: его квадрат определяется выражением , где s - С. к. ч. (называемое часто просто спином). Проекция вектора s на произвольное направление z также квантуется: для частиц с ненулевой массой (где ms - магнитное спиновое число), т. е. принимает 2s + 1 значений. Число s может принимать целые, нулевые или полуцелые значения.

6

Принцип неразличимости тождественных частиц в квантовой механике. Симметричные и антисимметричные состояния тождественных микрочастиц. Фермионы и бозоны. Принцип Паули.

Основа квантовой статистики – принципиальная неразличимость одинаковых частиц. Перестановка местами двух квантовых частиц не приводит к новому микросостоянию. Волновые ф-ии должны быть симметричными или антисимметричными по отношению к перестановке любой пары частиц, причем первый случай имеет место для частиц с целым спином, а второй с полуцелым. Для системы частиц, описывающейся антисимметричными ф-ями справедлив принцип Паули: в каждом квантовом состоянии может находиться одновременно не более одной частицы. Статистика, основанная на этом принципе, называется статистикой Ферми-Дирака. Частицы , подчиняющиеся этой статистике – фермионы. К их числу относят все частицы с полуцелым спином. Статистика Бозе-Эйнштейна, ктр. подчиняются частицы с целым спином. Частицы подчиняющиеся этой статистике – бозоны. Не выполняется принцип Паули; вероятность Р возникновения бозона в состоянии, в ктр. уже имеется n частиц, пропорциональна n. Обе статистики подчиняются принципу тождественности одинаковых микрочастиц.

Бозо́н (от фамилии физика Бозе) — частица с целым значением спина. Термин был предложен физиком Полем Дираком[1]. Бозоны, в отличие от фермионов, подчиняются статистике Бозе — Эйнштейна, которая допускает, чтобы в одном квантовом состоянии могло находиться неограниченное количество одинаковых частиц. Системы из многих бозонов описываются симметричными относительно перестановок частиц волновыми функциями. Различают элементарные бозоны и составные.

Фермио́н — частица (или квазичастица) с полуцелым значением спина. Своё название получили в честь физика Энрико Ферми.

Примеры фермионов: кварки (они образуют протоны и нейтроны, которые также являются фермионами), лептоны (электроны, мюоны, тау-лептоны, нейтрино), дырки (квазичастицы в полупроводнике)[1].

Фермионы подчиняются статистике Ферми — Дирака: в одном квантовом состоянии может находиться не более одной частицы (принцип Паули). Принцип запрета Паули ответственен за устойчивость электронных оболочек атомов, делая возможным существование сложных химических элементов. Он также позволяет существовать вырожденной материи под действием высоких давлений (нейтронные звёзды). Волновая функция системы одинаковых фермионов антисимметрична относительно перестановки двух любых фермионов. Квантовая система, состоящая из нечётного числа фермионов, сама является фермионом (например, ядро с нечётным массовым числом A; атом или ион с нечётной суммой A и числа электронов).

Порядок заполнения электронных состояний определяется двумя принципами:

принцип Паули: в атоме может быть только один электрон с данным набором квантовых чисел;

принцип минимума энергии: в основном состоянии атома электрон занимает квантовое состояние с наинизшей возможной энергией. Следует учесть, что вследствие взаимодействия электронов друг с другом значения энергии зависят не только от главного квантового числа n, но и от орбитального l.

При заполнении электронных слоёв атома в стационарном (невозбуждённом) состоянии выдерживается принцип наименьшей энергии электрона, в соответствии с которым

наиболее устойчивому состоянию электрона в атоме отвечает минимальная из возможных энергия этого электрона.

Поэтому заполнение электронных слоёв начинается с уровней, характеризующихся самой низкой энергией.

Русский учёный В. М. Клечковский установил, что энергия электрона возрастает по мере увеличения суммы главного и орбитального квантовых чисел (n + l). В соответствии с правилом Клечковского

заполнение электронных слоёв происходит в порядке увеличения сумм главного и орбитального квантовых чисел (n + l).

Рентгеновские спектры, возникающие при бомбардировке электронами антикатода рентгеновской трубки, бывают двух видов: сплошные и линейчатые. Сплошные спектры возникают при торможении быстрых электронов в веществе антикатода и являются обычным тормозным излучением электронов. Вид этих спектров не зависит от материала антикатода.

При повышении напряжения на трубке наряду со сплошным спектром появляется линейчатый. Он состоит из

Рис.13.5.

отдельных линий и зависит от материала антикатода. Каждый элемент обладает своим, характерным для него линейчатым спектром. Поэтому такие спектры называют характеристическими (рис. 13.5) .

С увеличением напряжения на рентгеновской трубке коротковолновая граница сплошного спектра смещается, линии же характеристического спектра становятся лишь более интенсивными, не меняя своего расположения.

Особенности характеристических спектров.

1. В отличие от оптических линейчатых спектров с их сложностью и разнообразием, рентгеновские характеристические спектры различных элементов отличаются простотой и однообразием. С ростом атомного номера Z элемента они монотонно смещаются в коротковолновую сторону. Законы Стефана — Больцмана и смещения Вина Из закона Кирхгофа следует, что спектральная плотность энергетическое светимости черного тела является универсальное функцией, поэтому нахождение ее явной зависимости от частоты и температуры является важной задачей теории теплового излучения.

2. Характеристические спектры разных элементов имеют сходный характер (однотипны) и не меняются, если интересующий нас элемент находится в соединении с другими. Это можно объяснить лишь тем, что характеристические спектры возникают при переходах электронов во внутренних частях атома, частях, имеющих сходное строение.

3. Характеристические спектры состоят из нескольких серий: К, L, М, ... Каждая серия — из небольшого числа линий: Ка, Кβ, Кγ, ... La, Lβ, Ly, ... и т. д. в порядке убывания длины волны λ.

7

лектронная конфигурация в несколько атомов электронов определяется тремя факторами. а) привлечение из ядра б) отталкивание между электронами и в) выталкивающей силы оказываемого пространство материи (см. структуру атома ). Когда атом находится в сильном электрическом поле, или магнитное поле, его электронная конфигурация смещается от своего первоначального состояния. То есть, из-за влияния внешнего поля, некоторые электроны в атоме (в основном, внешние электроны) смещаются от своего первоначального оболочек. Когда такой атом возбуждается, атом может излучать различных линий спектра по сравнению с оригинальной линии спектра. Этот эффект является прямым показанием для напряженности поля. То есть, при слабом поле влияет на внешние электроны только сильное поле может влиять как на внутренние и внешние электроны одинаково. Легких элементов может продемонстрировать этот эффект в слабом поле, чем сравнительно более тяжелые элементы, так как обязательную силу на электроны в легких элементов значительно меньше, чем у более тяжелых элементов.

Пашена — Бака эффект, эффект, состоящий в том, что в сильных магнитных полях сложное зеемановское расщепление спектральных линий переходит в простое (см. Зеемана эффект). Сильными следует считать магнитные поля, вызывающие зеемановское расщепление, сравнимое с мультиплетным расщеплением уровней энергии (см. Мультиплетность) и превосходящее его. В таких полях и происходит упрощение картины расщепления — вместо сложной картины наблюдается расщепление на 3 составляющие. П. — Б. э. впервые обнаружили немецкие физики Ф. Пашен и Э. Бак (Е. Back) в 1912.

Зеемана эффект, расщепление спектральных линий под действием магнитного поля. Открыто в 1896 П. Зееманом при исследовании свечения паров натрия в магнитном поле. Для наблюдения З. э. источник света, испускающий линейчатый спектр, располагается между полюсами мощного электромагнита (рис. 1). При этом каждая спектральная линия расщепляется на несколько составляющих. Расщепление весьма незначительно (для магнитных полей ~ 20 кэ составляет несколько десятых ), поэтому для наблюдения З. э. применяют спектральные приборы с высокой разрешающей способностью.

Эффе́кт Зе́емана — расщепление линий атомных спектров в магнитном поле.

Обнаружен в 1896 г. Зееманом для эмиссионных линий натрия.

Эффект обусловлен тем, что в присутствии магнитного поля квантовая частица, обладающая спиновым магнитным моментом, приобретает дополнительную энергию пропорциональную его магнитному моменту Приобретённая энергия приводит к снятию вырождения атомных состояний по магнитному квантовому числу и расщеплению атомных линий.

8

Химическая связь — явление взаимодействия атомов, обусловленное перекрыванием электронных облаков связывающихся частиц, которое сопровождается уменьшением полной энергии системы.

Энергетический уровень — собственные значения энергии квантовых систем, то есть систем, состоящих из микрочастиц (электронов, протонов и других элементарных частиц) и подчиняющихся законам квантовой механики. Каждый уровень характеризуется определённым состоянием системы, или подмножеством таковых в случае вырождения. Понятие применимо к атомам (электронные уровни), молекулам (различные уровни, соответствующие колебаниям и вращениям), атомным ядрам (внутриядерные энергетические уровни) и т.д.

Молекула — наименьшая частица вещества, состоящая из одинаковых или различных атомов, соединенных между собой химическими связями, и являющаяся носителем его основных химических и физических свойств. Химические связи обусловлены взаимодействием внешних, валентных электронов атомов. Наиболее часто в молекулах встречается два типа связи: ионная и ковалентная.

Ионная связь (например, в молекулах NaCl, KBr) осуществляется электростатическим взаимодействием атомов при переходе электрона одного атома к другому, т. е. при образовании положительного и отрицательного ионов. Ковалентная связь (например, в молекулах H2, С2, СО) осуществляется при обобществлении валентных электронов двумя соседними атомами (спины валентных электронов должны быть антипараллельны). Ковалентная связь объясняется на основе принципа неразличимости тождественных частиц, например электронов в молекуле водорода. Неразличимость частиц приводит к специфическому взаимодействию между ними, называемому обменным взаимодействием. Это чисто квантовый эффект, не имеющий классического объяснения, но его можно себе представить так, что электрон каждого из атомов молекулы водорода проводит некоторое время у ядра другого атома и, следовательно, осуществляется связь обоих атомов, образующих молекулу. При сближении двух водородных атомов до расстояний порядка боровского радиуса возникает их взаимное притяжение и образуется устойчивая молекула водорода.

Молекула является квантовой системой; она описывается уравнением Шредингера, учитывающим движение электронов в молекуле, колебания атомов молекулы, вращение молекулы. Решение этого уравнения — очень сложная задача, которая обычно разбивается на две: для электронов и ядер.

Энергия изолированной молекулы

(230.1)

где Еэл — энергия движения электронов относительно ядер, Екол — энергия колебаний ядер (в результате которых периодически изменяется относительное положение ядер), Евращ — энергия вращения ядер (в результате которых периодически изменяется ориентация молекулы в пространстве). В формуле (230.1) не учтены энергия поступательного движения центра масс молекулы и энергия ядер атомов в молекуле. Первая из них не квантуется, поэтому ее изменения не могут привести к возникновению молекулярного спектра, а вторую можно не учитывать, если не рассматривать сверхтонкую структуру спектральных линий. Отношения Еэл : Екол : Евращ = 1 : : т/М, где т — масса электрона, М — величина, имеющая порядок массы ядер атомов в молекуле, т/М»10–5¸10–3. Поэтому Еэл >> Екол >> Евращ. Доказано, что Еэл»1¸10 эВ, Екол»10–2¸10–1 эВ, Евращ »10–5¸10–3 эВ.

Каждая из входящих в выражение (230.1) энергий квантуется (ей соответствует набор дискретных уровней энергии) и определяется квантовыми числами. При переходе из одного энергетического состояния в другое поглощается или испускается энергия DE=hn. При таких переходах одновременно изменяются энергия движения электронов, энергии колебаний н вращения. Из теории и эксперимента следует, что расстояние между вращательными уровнями энергии DEвращ гораздо меньше расстояния между колебательными уровнями DEкол которое, в свою очередь, меньше расстояния между электронными уровнями DEэл. На рис. 308 схематически представлены уровни энергии двухатомной молекулы (для примера рассмотрены только два электронных уровня — показаны жирными линиями).

9

Комбинационное рассеяние света (эффект Рамана) — неупругое рассеяние оптического излучения на молекулах вещества (твёрдого, жидкого или газообразного), сопровождающееся заметным изменением частоты излучения. В отличие от рэлеевского рассеяния, в случае комбинационного рассеяния света в спектре рассеянного излучения появляются спектральные линии, которых нет в спектре первичного (возбуждающего) света. Число и расположение появившихся линий определяется молекулярным строением вещества.

Спектроскопия комбинационного рассеяния света (или рамановская спектроскопия) — эффективный метод химического анализа, изучения состава и строения веществ.

комбинационное рассеяние света сокр., КР; КРС иначе эффект комбинационного рассеяния; рамановское рассеяние; эффект Рамана (англ. Raman effect или Raman scattering) — неупругое рассеяние света (с изменением частоты/длины волны), сопровождающееся переходами вещества между колебательными уровнями энергии.

Описание

Рассеяние света, при котором происходит обмен энергией между фотонами и веществом, называется неупругим рассеянием или комбинационным рассеянием (эффектом Рамана). Следствием изменения энергии фотонов является изменение длины волны (частоты) рассеянного света. Наблюдается также упругое рассеяние света веществом, без изменения энергии фотонов и, следовательно, длины световой волны. Пример упругого рассеяния — релеевское рассеяние света (эффект Релея).

Механизм комбинационного рассеяния (КР) поясняет рис. 1. Стоксово КР характеризуется тем, что в процессе взаимодействия с молекулой фотон отдает ей часть энергии. В результате такого процесса молекула переходит с уровня с меньшим значением энергии на уровень с более высоким значением энергии, а энергия рассеянного фотона уменьшается (длина волны увеличивается (рис. 1, слева)). Антистоксово КР характеризуется тем, что в процессе взаимодействия с молекулой, находящейся в возбужденном состоянии, энергия фотона увеличивается, а молекула переходит в состояние с меньшим значением энергии (рис. 1, справа). Для сравнения на рис. 1 в центре приведена диаграмма, соответствующая релеевскому рассеянию, когда обмена энергией между фотоном и молекулой не происходит. На рис. 1 б также показан виртуальный уровень энергии молекулы в поле световой волны (верхняя пунктирная линия).

Так как при термодинамическом равновесии заселенность уровней уменьшается с увеличением энергии, то при спонтанном КР частота антистосковых переходов меньше частоты стоксовых — поэтому интенсивность стоксовых линий КР в спектре выше. Стоксовы линии КР расположены в спектре с «красной» стороны (со стороны больших длин волн/меньших частот) от релеевской линии. Не все переходы между различными колебательными энергетическими уровнями возможны.

Интенсивность комбинационного рассеяния (КР) на 3–6 порядков ниже релеевского, поэтому для наблюдения КР спектров требуется интенсивный источник монохроматического излучения и высокочувствительный детектор. В настоящее время в качестве источников излучения, главным образом, используют лазеры. КР-спектроскопия может быть использована для изучения структуры и состава вещества, его взаимодействия с окружающей средой. Полосы комбинационного рассеяния можно характеризовать частотой, интенсивностью и степенью деполяризации излучения. При облучении оптически анизотропных молекул поляризованным светом рассеянный свет окажется частично деполяризованным.

Когда частота возбуждающего света приближается и совпадает с частотой оптического перехода системы, реализуется ситуация резонансного КР (РКР). Спектральные особенности КР света дают информацию о типе структуры и взаимодействии электронной и фононной подсистем в полупроводниках.

КР света в конденсированных средах обладает рядом особенностей, так как в твердых телах колебания молекул (атомов, ионов) сильно коррелированны и, в случае кристаллов, их следует рассматривать как колебания кристаллической решетки в целом.

Спектры КР света аморфных твердых тел более «размыты», чем кристаллических — из-за разупорядочения структуры и уменьшения областей пространственных корреляций между колебаниями частиц (рис. 2). Наблюдается заметное уширение линий и в КР спектрах твердых растворов и высокодефектных кристаллов.

К уширению линий спектров может приводить ориентационное разупорядочение твердых тел, связанное с вариациями ориентации молекул в молекулярных кристаллах, диполей в сильно полярных кристаллах, свободных электронных пар в ионах типа Pb2+. Смещение линий КР спектров силикатных стекол служит мерой степени полимеризации силикатных сеток.

Спектроскопия КР является очень информативным методом для исследования наноматериалов, в частности, углеродных нанотрубок: можно определить их геометрические параметры, тип проводимости и т. д.

При нагревании веществ интенсивность антистоксовых линий КР заметно возрастает (в отличие от стоксовых), что позволяет использовать этот эффект для измерения температуры (разработаны соответствующие волоконно-оптические датчики).

При возбуждении КР источниками большой мощности вероятность стоксова рассеяния возрастает, и возникает вынужденное комбинационное рассеяние (ВКР). В волоконно-оптической связи широко используют ВКР усилители. ВКР лазеры позволяют получать мощное когерентное излучение в спектральных диапазонах, в которых нет эффективных лазеров другого типа.

КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА - рассеяние света в газах, жидкостях и кристаллах, сопровождающееся заметным изменением его частоты. В отличив от рэлеевского рассеяния света, при К. р. с. в спектре рассеянного излучения наблюдаются спектральные линии, отсутствующие в линейчатом спектре первичного (возбуждающего) света. Число и расположение появляющихся линий (наз. комбинационными линиями или спутниками) определяется молекулярным строением вещества. К. р. с. открыто в 1928 Г. С. Ландсбергом и Л. И. Мандельштамом при исследовании рассеяния света в кристаллах и одновременно Ч. В. Раманом и К. С. Кришнаном при исследовании рассеяния света в жидкостях [1, 2]. В зарубежной литературе К. р. с. обычно наз. эффектом Рамана. Спектроскопия К. р. с.- эфф. метод изучения состава и строения вещества.

Общие закономерности. Спектры К. р. с. получают с помощью спец. оптич. установки, в к-рой интенсивный пучок света концентрируют на изучаемом объекте (рис. 1). В качестве источника света до 60-х гг. чаще всего применялись ртутные лампы, затем их вытеснили лазеры. Рассеянный свет наблюдается под углом рассеяния (обычно =90°) к направлению падающего луча. Спектры К. р. с. регистрируются фотографич. или фотоэлектрич. методом.

Как отмечалось нами, атомы могут находиться лишь в квантовых состояниях с дискретными значениями энергии Е1, Е2, Е3, ... Ради простоты рассмотрим только два из этих состояний (1 и 2) с энергиями Е1 и Е2. Если атом находится в основном состоянии 1, то под действием внешнего излучения может осуществиться вынужденный переход в возбужденное состояние 2 (рис. 309, а), приводящий к поглощению излучения. Вероятность подобных переходов пропорциональна плотности излучения, вызывающего эти переходы.

Атом, находясь в возбужденном состоянии 2, может через некоторый промежуток времени спонтанно, без каких-либо внешних воздействий, перейти в состояние с низшей энергией (в нашем случае в основное), отдавая избыточную энергию в виде электромагнитного излучения (испуская фотон с энергией hn=E2–Е1). Процесс испускания фотона возбужденным атомом (возбужденной микросистемой) без каких-либо внешних воздействий называется спонтанным (или самопроизвольным) излучением (рис. 309, б). Чем больше вероятность спонтанных переходов, тем меньше среднее время жизни атома в возбужденном состоянии. Так как спонтанные переходы взаимно не связаны, то спонтанное излучение некогерентно.

В 1916 г. А. Эйнштейн для объяснения наблюдавшегося на опыте термодинамического равновесия между веществом и испускаемым и поглощаемым им излучением постулировал, что помимо поглощения и спонтанного излучения должен существовать третий, качественно иной тип взаимодействия. Если на атом, находящийся в возбужденном состоянии 2, действует внешнее излучение с частотой, удовлетворяющей условию hv=E2–E1, то возникает вынужденный (индуцированный) переход в основное состояние 1 с излучением фотона той же энергии hv=E2–E1 (рис. 309, в). При подобном переходе происходит излучение атомом фотона, дополнительно к тому фотону, под действием которого произошел переход. Возникающее в результате таких переходов излучение называется вынужденным (индуцированным) излучением. Таким образом, в процесс вынужденного излучения вовлечены два фотона: первичный фотон, вызывающий испускание излучения возбужденным атомом, и вторичный фотон, испущенный атомом. Существенно, что вторичные фотоны неотличимы от первичных, являясь точной их копией.

В статистической физике известен принцип детального равновесия, согласно которому при термодинамическом равновесии каждому процессу можно сопоставить обратный процесс, причем скорости их протекания одинаковы. А. Эйнштейн применил этот принцип и закон сохранения энергии при рассмотрении излучения и поглощения электромагнитных волн в случае черного тела. Из условия, что при равновесии полная вероятность испускания (спонтанного и вынужденного) фотонов равна вероятности поглощения фотонов той же частоты, Эйнштейн получил выведенную ранее Планком формулу (200.3).

Эйнштейн и Дирак показали, что вынужденное излучение (вторичные фотоны) тождественно вынуждающему излучению (первичным фотонам): оно имеет такие же частоту, фазу, поляризацию и направление распространения, как и вынуждающее излучение. Следовательно, вынужденное излучение строго когерентно с вынуждающим излучением, т. е. испущенный фотон неотличим от фотона, падающего на атом.

Испущенные фотоны, двигаясь в одном направлении и встречая другие возбужденные атомы, стимулируют дальнейшие индуцированные переходы, и число фотонов растет лавинообразно. Однако наряду с вынужденным излучением возможен и конкурирующий процесс — поглощение. Поэтому для усиления падающего излучения необходимо, чтобы число актов вынужденного излучения фотонов (оно пропорционально заселенности возбужденных состояний) превышало число актов поглощения фотонов (оно пропорционально заселенности основных состояний). В системе атомов, находящейся в термодинамическом равновесии, поглощение падающего излучения будет преобладать над вынужденным, т. е. падающее излучение при прохождении через вещество будет ослабляться.

Чтобы среда усиливала падающее на нее излучение, необходимо создать неравновесное состояние системы, при котором число атомов в возбужденных состояниях было бы больше, чем их число в основном состоянии. Такие состояния называются состояниями с инверсией населенностей. Процесс создания неравновесного состояния вещества (перевод системы в состояние с инверсией населенностей) называется накачкой. Накачку можно осуществить оптическими, электрическими и другими способами.

В средах с инверсными состоящими вынужденное излучение может превысить поглощение, вследствие чего падающий пучок света при прохождении через эти среды будет усиливаться (эти среды называются активными). В данном случае явление протекает так, как если бы в законе Бугера I=I0e–ax (см. (187.1)) коэффициент поглощения a, зависящий, в свою очередь, от интенсивности излучения, стал отрицательным. Активные среды поэтому можно рассматривать в качестве сред с отрицательным коэффициентом поглощения.

Впервые на возможность получения сред, в которых свет может усиливаться за счет вынужденного излучения, указал в 1939 г. российский физик В. А. Фабрикант, экспериментально обнаружив вынужденное излучение паров ртути, возбужденных при электрическом разряде. Открытие явления усиления электромагнитных волн и изобретенный способ их усиления (В. А. Фабрикант, М. М. Вудынский, Ф. А. Бугаева; 1951) легли в основу квантовой электроники, положения которой позволили впоследствии осуществить квантовые усилители и квантовые генераторы света.

10

Ядро атома состоит из нуклонов, которые подразделяются на протоны и нейтроны.

Символическое обозначение ядра атома:

А- число нуклонов, т.е. протонов + нейтронов ( или атомная масса )

Z- число протонов ( равно числу электронов )

N- число нейтронов ( или атомный номер )

N = A - Z

ЯДЕРНЫЕ СИЛЫ

- действуют между всеми нуклонами в ядре;

- силы притяжения;

- короткодействующие.

Нуклоны притягиваются друг к другу ядерными силами, которые совершенно непохожи ни на гравитационные, ни на электростатические. . Ядерные силы очень быстро спадают с расстоянием. Радиус их действия порядка 0,000 000 000 000 001 метра.

Для этой сверхмалой длины, характеризующей размеры атомных ядер, ввели специальное обозначение - 1 Фм ( в честь итальянского физика Э. Ферми, 1901-1954). Все ядра имеют размеры нескольких ферми. Радиус ядерных сил равен размеру нуклона, поэтому ядра - сгустки очень плотной материи. Возможно, самой плотной в земных условиях.

Ядерные силы - сильные взаимодействия. Они многократно превосходят кулоновскую силу (на одинаковом расстоянии). Короткодействие ограничивает действие ядерных сил. С ростом числа нуклонов ядра становятся неустойчивыми, и поэтому большинство тяжелых ядер радиоактивны, а совсем тяжелые вообще не могут существовать.

Конечное число элементов в природе - следствие короткодействия ядерных сил.

Масса и энергия связи ядра

Масса ядра измеряется в атомных единицах массы (а.е.м). За одну атомную единицу массы принимается 1/12 часть массы нейтрального атома углерода 12 С:

1а.е.м = 1.6606 10-27 кг.

А.е.м. выражается через энергетические единицы:

1а.е.м = 1.510-3 эрг = 1.510-10Дж = 931.49 МэВ

Масса ядра всегда меньше суммы масс составляющих его нуклонов.

Энергия связи ядра Eсв(A,Z) это минимальная энергия, необходимая, чтобы развалить ядро на отдельные, составляющие его нуклоны.

Есв(A, Z) = [Z mp + (A - Z)mn - M(A, Z)]c2,

где Z - число протонов, ( A - Z) - число нейтронов, mp - масса протона, mn - масса нейтрона, М(A,Z) - масса ядра с массовым числом А и зарядом Z.

Энергия связи ядра, выраженная через массу атома Mат, имеет вид:

Есв(A, Z) = [ZmH + (A - Z)mn - Mат(A, Z)]c2 ,

где mH - масса атома водорода.

Рис. 1

Удельная энергия связи ядра ε(A, Z) это энергия связи, приходящаяся на один нуклон

ε(A, Z) = Eсв(A,Z) / A.

На рис. 1 показана зависимость удельной энергии связи ядра ε от числа нуклонов A. Видно, что наиболее сильно связаны ядра в районе железа и никеля (A ~ 55-60). Такой ход зависимости ε(A) показывает, что для легких ядер энергетически выгодны реакции синтеза более тяжелых ядер, а тяжелых - деление на более легкие осколки.

Избыток масс Δ связан с массой атома Mат(A,Z) и массовым числом A соотношением:

Δ = Мат(A,Z) - А.

Ядерные силы — это силы, удерживающие нуклоны в ядре, представляющие собой большие силы притяжения, действующие только на малых расстояниях. Они обладают свойствами насыщения, в связи с чем ядерным силам приписывается обменный характер (с помощью пи-мезонов). Ядерные силы зависят от спина, не зависят от электрического заряда и не являются центральными силами[2].

11

Радиоактивность – самопроизвольные превращения атомных ядер, сопровождающиеся испусканием элементарных частиц или более лёгких ядер. Ядра, подверженные таким превращениям, называют радиоактивными, а процесс превращения – радиоактивным распадом.

Радиоактивный распад возможен только тогда, когда он энергетически выгоден, т.е. сопровождается выделением энергии. Условием этого является превышение массы М исходного ядра суммы масс mi продуктов распада, т.е. неравенство

M >∑mi.

Из около 3000 известных ядер (большинство из них получено искусственно) лишь 264 не являются радиоактивными. Основными видами радиоактивного распада являются альфа-распад (испускание ядрами альфа-частиц), бета-распад (испускание (или поглощение) электрона, а также антинейтрино, или испускание позитрона и нейтрино), гамма-распад (испускание гамма-квантов) и спонтанное деление (распад ядра на два осколка сравнимой массы). К более редким видам радиоактивного распада относятся испускание ядрами одного или двух нуклонов, а также испускание фрагментов (кластеров) – лёгких ядер от 12С до 32S. Во всех видах радиоактивности (кроме гамма-радиоактивности) изменяется состав ядра – число протонов Z , массовое число А или и то и другое.

Важнейшей характеристикой радиоактивности является закон радиоактивного распада, показывающий как со временем t изменяется (в среднем) число N радиоактивных ядер в образце

N(t) = N0e–λt,

где N0 – число исходных ядер в начальный момент (момент их образования или начала наблюдения), а λ – постоянная распада (вероятность распада радиоактивного ядра в единицу времени). Через эту постоянную можно выразить среднее время жизни радиоактивного ядра τ = 1/λ, а также период полураспада T1/2 = ln2/τ. Период полураспада наглядно характеризует скорость распада, показывая за какое время число радиоактивных ядер в образце уменьшится вдвое.

Следует подчеркнуть, что процесс радиоактивного распада (как и все процессы в микромире) это случайный процесс и можно говорить лишь о вероятности его протекания. Так если в образце N радиоактивных ядер, то в единицу времени не обязательно произойдёт λN актов радиоактивного распада. Это число может быть и больше и меньше λN, которое в данном случае является лишь средним (математическим ожиданием).

На характеристики радиоактивного распада, в частности его скорость (период полураспада), оказывают существенное влияние силы (взаимодействия), вызывающие распад. Альфа-распад изначально вызывается сильным взаимодействием, но его скорость определяется кулоновским барьером (электромагнитным взаимодействием). Бета-распад вызывается слабым взаимодействием, а гамма-распад – электромагнитным.

Явление радиоактивности открыто в 1896 г. А. Беккерелем. В 1899 г. Э. Резерфорд открыл, что уран излучает положительно заряженные частицы (α-частицы) и отрицательно заряженные β-частицы (электроны). В 1900 г. П. Виллард открыл нейтральные частицы (γ-кванты) при изучении распада урана. Спонтанное деление ядер открыто в 1940 г. К.А. Петржаком и Г.Н. Флёровым.

Радиоактивность

Явление самопроизвольного испускания химическими элементами излучения, обладающего значительной проникающей способностью и ионизирующими свойствами, получило название естественной радиоактивности. Элементы, испускающие такое излучение называются радиоактивными.

Радиоактивными являются все элементы с порядковым номером более 83 в таблице Менделеева.(Z >83).

Состав радиоактивного излучения

Излучение радиоактивных веществ состоит из трех компонент: a-,b-,g-излучения. Обнаружено, что a-,b-лучи отклоняются магнитным полем в разные стороны, а g-лучи не отклоняются совсем. Так были определены знаки зарядов составных частей радиоактивного излучения. Результаты исследования свойств излучения приведены в таблице

Обозначение	Природа	Зарядовое и массовое число	Энергия	cкорость
a-лучи	поток полностью ионизированных атомов гелия	2a4 или  2He4	4-9 МэВ	107 м/c
b-лучи	поток быстрых электронов	-1b0 или-1е0	непрерывный спектр энергий от 0 до 782 кэВ	108 м/с
g-лучи	жесткое электромагнитное излучение (l=10-2 нм		линейчатый спектр энергий	3·108 м/с

Закон радиоактивного распада — закон, открытый Фредериком Содди и Эрнестом Резерфордом экспериментальным путём и сформулированный в 1903 году. Современная формулировка закона:

что означает, что число распадов за интервал времени t в произвольном веществе пропорционально числу имеющихся в образце атомовN .

В этом математическом выражении — постоянная распада, которая характеризует вероятность радиоактивного распада за единицу времени и имеющая размерность с−1. Знак минус указывает на убыль числа радиоактивных ядер со временем.

Этот закон считается основным законом радиоактивности, из него было извлечено несколько важных следствий, среди которых формулировки характеристик распада — среднее время жизни атома и период полураспада

12

эффект Мёссбауэра (англ. Mössbauer effect) — явление резонансного поглощения гамма-квантов атомными ядрами без потери энергии на отдачу импульса.

Описание

Ядра атомов могут находиться в основном и возбужденном состояниях. Переход ядра из одного состояния в другое сопровождается либо поглощением, либо испусканием гамма-кванта коротковолнового рентгеновского излучения (рис. а). Энергия гамма-кванта определяется разностью энергий между основным и возбужденным состояниями ядра атома (ET ), энергией отдачи ядра (R ~ 10–1 эВ для свободных атомов) и допплеровским сдвигом (D), вызванным поступательным движением ядра:

Eиспускания = EТ – R± D (энергия гамма-квантов, испускаемых источником),

Eпоглощения = EТ + R ± D (энергия гамма-квантов, поглощаемых образцом).

Условие резонанса достигается тогда, когда испускаемый возбужденным ядром гамма-квант будет поглощен ядром, находящимся в основном состоянии:

Eиспускания ≈ Eпоглощения.

Графически такое условие может быть представлено в виде области перекрывания площадей кривых распределения по энергиям испускаемых и поглощаемых квантов (рис. б). Вероятность резонансного процесса возрастает, если ядро-излучатель и ядро-поглотитель фиксированы в жесткой кристаллической решетке. В этом случае при поглощении фотона энергия отдачи превращается в энергию колебаний кристаллической решетки, т. е. отдачу испытывает все твердое тело. Принимая во внимание, что масса тела бесконечно велика по сравнению с массой отдельного атома, энергия отдачи становится пренебрежимо малой (R ~ 10–4 эВ).

Эффект резонанса, как правило, наблюдается только в твердом теле для ядер стабильных изотопов (их насчитывается около 80), наиболее широкое применение среди которых нашли Fe57 и Sn119. Измерения вероятности эффекта Мёссбауэра и ее зависимости от температуры позволяют получить сведения об особенностях взаимодействия атомов в твердых телах и колебаниях кристаллической решетки. Благодаря этому мессбауровский эффект широко применяется как метод исследования твердых тел (см. спектроскопия, мёессбауэровская).

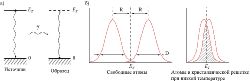
Иллюстрации а — Схема резонансного поглощения гамма-кванта; б — распределение испускаемых и поглощаемых гамма-квантов по энергиям.\

Я́дерная реа́кция — процесс образования новых ядер или частиц при столкновениях ядер или частиц. Впервые ядерную реакцию наблюдал Резерфорд в 1919 году, бомбардируя α-частицами ядра атомов азота, она была зафиксирована по появлению вторичных ионизирующих частиц, имеющих пробег в газе больше пробега α-частиц и идентифицированных как протоны. Впоследствии с помощью камеры Вильсона были получены фотографии этого процесса.

По механизму взаимодействия ядерные реакции делятся на два вида:

реакции с образованием составного ядра, это двухстадийный процесс, протекающий при не очень большой кинетической энергии сталкивающихся частиц (примерно до 10 МэВ).

прямые ядерные реакции, проходящие за ядерное время, необходимое для того, чтобы частица пересекла ядро. Главным образом такой механизм проявляется при больших энергиях бомбардирующих частиц.

Если после столкновения сохраняются исходные ядра и частицы и не рождаются новые, то реакция является упругим рассеянием в поле ядерных сил, сопровождается только перераспределением кинетической энергии и импульса частицы и ядра-мишени и называется потенциальным рассеянием[1][2].

Законы сохранения в ядерных реакциях

При ядерных реакциях выполняются все законы сохранения классической физики. Эти законы накладывают ограничения на возможность осуществления ядерной реакции. Даже энергетически выгодный процесс всегда оказывается невозможным, если сопровождается нарушением какого-либо закона сохранения. Кроме того, существуют законы сохранения, специфичные для микромира; некоторые из них выполняются всегда, насколько это известно (закон сохранения барионного числа, лептонного числа); другие законы сохранения (изоспина, чётности, странности) лишь подавляют определённые реакции, поскольку не выполняются для некоторых из фундаментальных взаимодействий. Следствиями законов сохранения являются так называемые правила отбора, указывающие на возможность или запрет тех или иных реакций.

[править]

Закон сохранения энергии

Если , , , — полные энергии двух частиц до реакции и после реакции, то на основании закона сохранения энергии:

При образовании более двух частиц соответственно число слагаемых в правой части этого выражения должно быть больше. Полная энергия частицы равна её энергии покоя Mc2 и кинетической энергии E, поэтому:

Разность суммарных кинетических энергий частиц на «выходе» и «входе» реакции Q = (E3 + E4) − (E1 + E2) называется энергией реакции (или энергетическим выходом реакции). Она удовлетворяет условию:

Множитель 1/c2 обычно опускают, при подсчёте энергетического баланса выражая массы частиц в энергетических единицах (или иногда энергии в массовых единицах).

Если Q > 0, то реакция сопровождается выделением свободной энергии и называется экзоэнергетической, если Q < 0, то реакция сопровождается поглощением свободной энергии и называется эндоэнергетической.

Легко заметить, что Q > 0 тогда, когда сумма масс частиц-продуктов меньше суммы масс исходных частиц, то есть выделение свободной энергии возможно только за счёт снижения масс реагирующих частиц. И наоборот, если сумма масс вторичных частиц превышает сумму масс исходных, то такая реакция возможна только при условии затраты какого-то количества кинетической энергии на увеличение энергии покоя, то есть масс новых частиц. Минимальное значение кинетической энергии налетающей частицы, при которой возможна эндоэнергетическая реакция, называется пороговой энергией реакции. Эндоэнергетические реакции называют также пороговыми реакциями, поскольку они не происходят при энергиях частиц ниже порога.

[править]

Закон сохранения импульса

Полный импульс частиц до реакции равен полному импульсу частиц-продуктов реакции. Если , , , — векторы импульсов двух частиц до реакции и после реакции, то

Каждый из векторов может быть независимо измерен на опыте, например, магнитным спектрометром. Экспериментальные данные свидетельствуют о том, что закон сохранения импульса справедлив как при ядерных реакциях, так и в процессах рассеяния микрочастиц.

[править]

Закон сохранения момента импульса

Момент количества движения также сохраняется при ядерных реакциях. В результате столкновения микрочастиц образуются только такие составные ядра, момент импульса которых равен одному из возможных значений момента, получающегося при сложении собственных механических моментов (спинов) частиц и момента их относительного движения (орбитального момента). Каналы распада составного ядра также могут быть лишь такими, чтобы сохранялся суммарный момент количества движения (сумма спинового и орбитального моментов).

[править]

Другие законы сохранения

при ядерных реакциях сохраняется электрический заряд — алгебраическая сумма элементарных зарядов до реакции равна алгебраической сумме зарядов после реакции.

при ядерных реакциях сохраняется число нуклонов, что в самых общих случаях интерпретируется как сохранение барионного числа. Если кинетические энергии сталкивающихся нуклонов очень высоки, то возможны реакции рождения нуклонных пар. Поскольку нуклонам и антинуклонам приписываются противоположные знаки, то при любых процессах алгебраическая сумма барионных чисел всегда остаётся неизменной.

при ядерных реакциях сохраняется число лептонов (точнее, разность количества лептонов и количества антилептонов, см. Лептонное число).

при ядерных реакциях, которые протекают под воздействием ядерных или электромагнитных сил, сохраняется чётность волновой функции, описывающей состояние частиц до и после реакции. Чётность волновой функции не сохраняется в превращениях, обусловленных слабыми взаимодействиями[1].

при ядерных реакциях, обусловленных сильными взаимодействиями, сохраняется изотопический спин. Слабые и электромагнитные взаимодействия изоспин не сохраняют.

Античасти́ца — частица-двойник некоторой другой элементарной частицы, обладающая той же массой и тем же спином, но отличающаяся от неё знаками некоторых характеристик взаимодействия (зарядов, таких как электрический и цветовой заряды, барионное и лептонное квантовые числа).

Само определение того, что называть «частицей» в паре частица-античастица, в значительной мере условно. Однако при данном выборе «частицы» её античастица определяется однозначно. Сохранение барионного числа в процессах слабого взаимодействия позволяет по цепочке распадов барионов определить «частицу» в любой паре барион-антибарион. Выбор электрона как «частицы» в паре электрон-позитрон фиксирует (вследствие сохранения лептонного числа в процессах слабого взаимодействия) определение состояния «частицы» в паре электронных нейтрино-антинейтрино. Переходы между лептонами различных поколений (типа ) не наблюдались, так что определение «частицы» в каждом поколении лептонов, вообще говоря, может быть произведено независимо. Обычно по аналогии с электроном «частицами» называют отрицательно заряженные лептоны, что при сохранении лептонного числа определяет соответствующие нейтрино и антинейтрино. Для бозонов понятие «частица» может фиксироваться определением, например, гиперзаряда.

Чётность — свойство физической величины сохранять свой знак (или изменять на противоположный) при некоторых дискретных преобразованиях. Она выражается числом, принимающим два значения: +1 и −1.

A′ = P·A,

где

A, A′ — физическая величина до и после инверсии;

P — чётность величины A.

Чётность наиболее важна для квантовой физики, где она является одной из главных характеристик волновой функции. Соответственно, понятие чётности переносится и на частицу (атом, ядро), которую характеризует эта волновая функция.

Величины с положительной чётностью называются чётными, а с отрицательной — нечётными. Чётность величины зависит от её математической природы, а точнее от трансформационных свойств математического объекта, выражающего данную физическую величину, относительно инвертируемого параметра. Величины могут также не иметь определённой чётности относительно какого-либо конкретного преобразования.

Разновидности чётности, используемые в физике:

пространственная чётность P — соответствует инверсии пространства (координаты x y z меняются на –x –y -z );

временна́я чётность T — соответствует инверсии времени (направление течения времени меняется на обратное);

зарядовая чётность C — соответствует зарядовой инверсии (все частицы меняются на античастицы);

комбинированная чётность CP — соответствует одновременной зарядовой и пространственной инверсии;

G-чётность — особый параметр у истинно нейтральных частиц;

R-чётность (суперчётность) R — соответствует суперсимметричной инверсии (фермионы заменяются на бозоны и наоборот).

Чётность является мультипликативной величиной, то есть чётность системы, состоящей из неподвижных друг относительно друга частей, равна произведению чётностей составляющих.

Законы сохранения

Кинематической характеристикой частицы является 4-импульс (px,py,pz,iE), где px, py, pz − компоненты трехмерного вектора импульса, а Е − энергия частицы.

В процессах сильного взаимодействия сохраняются следующие величины:

1) 4-импульс ;

2) электрический заряд Q;

3) барионный заряд B;

4) лептонный заряд L (имеются три лептонных заряда Le, Lμ, Lτ);

5) спин J − собственный момент количества движения;

6) изотопический спин I;

7) странность s;

8) четность пространственная Р;

9) четность временная Т;

10) четность зарядовая С;

11) четность комбинированная СР и СРТ;

12) квантовые числа s (strange), с (charm), b (beauty), t (truth);

13) G-четность G.

В электромагнитных взаимодействиях не сохраняются G-четность и изотопический спин I, а в слабых взаимодействиях не сохраняются Р-четность, С-четность, Т-четность, G-четность и изотопический спин I.

Для наглядности все законы сохранения сведены в табл. 15. Знак + обозначает, что данная величина сохраняется.

Под изотопическим спином (изоспином) понимается квантовое число определяющее число зарядовых состояний адронов. Так например считается что протон и нейтрон (нуклоны) имеют одинаковый изотопический спин 1/2 и отличаются знаком проекции изотопического спина в особом изотопическом пространстве: когда проекция изотопического спина равна +1/2 нуклон становится протоном, а когда равна -1/2 нуклон становится нейтроном. Такая пара элементарных частиц называется изодублетом.

Второй пример для тройки (изотриплет) элементарных частиц пионов для них считается что изотопический спин равен 1 и получаются три проекции изотопического спина в особом изотопическом пространстве: +1, 0, -1, что соответствует пи+-мезону, пи0-мезону и пи--мезону.

Число элементарных частиц с изотопическим спином I в таком изотопическом мультиплете равно 2I+1.(Изодублет, изотриплет и т.д. называются изотопическими мультиплетами.)

C точки зрения сильного взаимодействия протон и нейтрон (равно как и тройка пионов) являются одинаковыми частицами, что выражает свойство изотопической инвариантности сильного взаимодействия. Считается что разница между элементарными частицами обусловлена электромагнитными взаимодействиями.

В квантовой механике уже есть квантовое число с аналогичными свойствами - спин, поэтому по аналогии и было введено новое квантовое число элементарных частиц - изотопический спин. Утверждается что им обладает каждая элементарная частица.

Утверждается что изотопический спин сохраняется во всех процессах обусловленных сильным взаимодействием и нарушается в электромагнитном и слабом взаимодействиях.

Античастицы

Свойства антипротона были предсказаны теоретиками еще во времена открытия позитрона. Однако для того, чтобы обнаружить эту частицу, необходимо было иметь ускоренные протоны с энергией больше 6 ГэВ. Такой ускоритель был специально построен, и начались эксперименты по обнаружению антипротона и антинейтрона. В 1955 году О. Чемберлену, Э. Сегре, К. Виганду и Т. Ипсилантису удалось получить и идентифицировать антипротоны, образующиеся в реакции

p + p → p + p + + p.

В 1956 году был открыт антинейтрон. Пятидесятые годы завершились открытием антигиперонов.

Сейчас почти ни у кого не вызывает сомнения тот факт, что каждая частица имеет "двойника" - античастицу. Античастицы обладают рядом характеристик, имеющих те же численные значения, что и частицы и некоторые характеристики с противоположным знаком. Так у частицы и античастицы одинаковые массы, спины, изоспины, времена жизни; противоположные знаки у электрических зарядов, магнитных моментов, барионных и лептонных зарядов, проекций изоспина, четности и др. Схемы распада частиц и античастиц - зарядово-сопряженные, например,

n → p + e- + e;

→ + e+ + e.

У истинно нейтральных частиц (γ, π0, η0) частица и античастица тождественны.

Наиболее сложной формой антивещества, полученной и идентифицированной в лабораторных условиях, являются антиядра трития, гелия. Эти эксперименты были выполнены на серпуховском ускорителе в 1970-74 гг. В 1998 году были получены первые атомы антиводорода.

Странные частицы

В течение 10 лет, последовавших за открытием пиона в 1947 году, в результате изучения космических лучей и экспериментов на вновь построенных ускорителях высоких энергий таблица элементарных частиц начала быстро пополняться новыми элементарными частицами. За это время их было открыто свыше 30. Первыми из открытых частиц были K-мезоны или каоны, частицы с массой ~500 МэВ. Затем были обнаружены тяжелые частицы Λ и Σ. Была обнаружена странная особенность вновь открытых частиц - они рождались парами, хотя не были частицей и античастицей. Здесь была другая закономерность. Так, например, при столкновении двух протонов возможна реакция

p + p → p + Λ + K+,

в которой рождаются две странные частицы -частица и K+-мезон. Образовавшиеся "странные" частицы затем распадались на лептоны, нуклоны и пионы

K+ → μ+ + νμ,

Λ → p + π-,

K+ → π+ + π0,

Λ → n + π0.

Вторая особенность поведения странных частиц - большое время жизни. В результате распада Λ образуются сильно взаимодействующие частицы p и или n и . Поэтому казалось, что время жизни странных частиц должно быть ~10-22-10-23 сек. На самом деле их время жизни ~10-10 сек, характерно для слабого взаимодействия. Для того, чтобы объяснить такое поведение странных частиц М. Гелл-Манн и К. Нишиджима высказали предположение, что странная частица является носителем еще одного нового квантового числа, которое было названо странностью. Странность сохраняется в сильных взаимодействиях, но не сохраняется в слабых взаимодействиях. Это позволило сразу объяснить и парное рождение странных частиц в реакции сильного взаимодействия и большое время жизни в результате распада, происходящего за счет слабого взаимодействия.

Среди вновь открытых странных частиц оказались частицы, имеющие массу покоя больше массы покоя нуклона. Эти частицы были названы гиперонами. К ним относятся Λ, Σ0, Σ+, Σ-, Ξ0, Ξ-,Ω-.

Резонансы

В начале шестидесятых годов был открыт еще один класс элементарных частиц, которые получили название резонансов или резонансных частиц. Время жизни их порядка 10-22 сек. Первый нуклонный резонанс был открыт Э. Ферми в 1952 году в реакциях рассеяния π-мезонов на нуклонах, он был назван Δ-изобарой. Резонансы стали активно исследоваться и открываться с развитием техники водородных пузырьковых камер, в которых стало возможно наблюдать продукты распада резонансов

Δ0 → p + π-, Δ++ → p + π+.

Впервые среди элементарных частиц появилась частица с зарядом +2.

Законы сохранения и симметрии

Важную роль в понимании механизмов взаимодействия элементарных частиц, их образования и распада сыграли законы сохранения. Законы сохранения определяют правила отбора, согласно которым процессы с частицами, приводящие к нарушению законов сохранения, не могут осуществляться в определенных типах взаимодействий. В дополнение к законам сохранения, действующим в макромире, в физике микромира были обнаружены новые законы сохранения, позволяющие объяснить наблюдаемые экспериментальные закономерности.

Законы сохранения являются результатом обобщения экспериментальных наблюдений. Часть из них была открыта в результате того, что реакции или распады, разрешенные всеми ранее известными законами сохранения, не наблюдались или оказывались сильно подавленными. Так были открыты законы сохранения барионного, лептонных зарядов, странности, чарма и др.

Установлено, что каждый закон сохранения связан с какой-либо симметрией в окружающем нас мире (теорема Нетер). Так законы сохранения энергии и импульса связанны с однородностью времени и пространства. Закон сохранения момента количества движения связан с симметрией пространства относительно вращений. Законы сохранения зарядов связаны с симметрией физических законов относительно специальных преобразований, описывающих частицы.

Слабые взаимодействия нарушают симметрии

Пространственная четность P характеризует поведение волновой функции при зеркальном отражении. Поэтому сохранение пространственной четности означает существование зеркальной симметрии. Если пространственная четность сохраняется, то для зеркально-симметричного процесса вероятность вылета продуктов под углами и - по отношению к некоторому выделенному направлению должны быть равны. Долгое время считалось, что четность замкнутой системы не меняется в результате происходящих в ней процессов и это справедливо для любых процессов.

Однако в 1956 году, анализируя распады K-мезонов, Ли Цзун-дао и Янг Джень-нин предположили, что в слабых взаимодействиях пространственная четность не сохраняется. Они предложили для проверки закона сохранения пространственной четности использовать -распад поляризованных ядер. Поляризация ядер позволяла фиксировать выделенное направление - спин ядра (спин ядра не меняется при инверсии координат). В 1957 году эксперимент по изучению -распада поляризованных ядер 60Сo был поставлен Ву Дзин-сюн. Оказалось, что электроны летят в основном в сторону противоположную направлению спина ядра. Таким образом несохранение четности для процессов, происходящих в результате слабого взаимодействия было экспериментально доказано. Оказалось, что мир не симметричен. И, в принципе, правое и левое можно различить. Был установлен конкретный вид нарушения пространственной четности. Оказалось, что частицы участвуют в слабых взаимодействиях своими левоспиральными компонентами. Это так называемый (V-A)-вариант Ферми.

В слабых взаимодействиях в отличие от сильных и электромагнитных также отсутствует симметрия относительно зарядового сопряжения - замены всех частиц на соответствующие античастицы. Однако, как впервые было указано Л. Ландау, Ли Цзун-дао и Янг Джень-нином в 1956 году в слабых взаимодействиях должна сохранятся комбинированная инверсия (CP-четность) - одновременная замена частиц на античастицы и зеркальное отражение.

Однако, в 1964 году В. Фитчем, Дж. Кронином, Р. Турле и Дж. Христенсоном в экспериментах по распаду K0-мезонов было обнаружено нарушение закона сохранения CP-четности. Однозначной теоретической интерпретации этого факта сегодня нет. В квантовой теории поля Людерсом и Паули была доказана CPT-теорема, согласно которой при любом взаимодействии произведения трех инверсий - пространственной, зарядовой и временной - инвариант. Исходя из CPT-теоремы и из не сохранения CP-четности, следует отсутствие симметрии относительно обращения времени в распадах K0-мезонов.

Кварки – частицы, из которых состоят адроны

К середине шестидесятых годов число обнаруженных сильновзаимодействующих элементарных частиц - адронов перевалило за 100. Возникла уверенность, что наблюдаемые частицы не отражают предельный элементарный уровень материи.

В 1964 году независимо друг от друга М. Гелл-Манн и Д. Цвейг предложили модель кварков - частиц, из которых могут состоять адроны. Появление такой модели было вполне естественным. Эксперименты по рассеянию электронов на нуклонах показали, что нейтрон и протон в отличие от электрона имеют сложную структуру. Поэтому гипотеза о новых фундаментальных частицах, из которых можно строить адроны, казалась вполне правдоподобной. Для того чтобы объяснить наблюдаемые свойства адронов, кваркам пришлось приписать довольно необычайные свойства. Кварки должны иметь дробный электрический заряд +2/3 или -1/3. Барионы "конструировались" из трех кварков, мезоны "конструировались" из кварка и антикварка. Все обнаруженные до 1974 г. адроны можно было описать, составляя их из кварков всего лишь трех типов - u, d, s. При этом трехкварковая модель адронов казалась достаточно замкнутой - практически каждой комбинации кварков соответствовала экспериментально наблюдаемая частица.

1974 год завершился для физиков сенсацией. Одновременно две группы физиков объявили о наблюдении новой частицы. Теперь ее называют . Масса обнаруженной частицы ~3.1 ГэВ. Причиной сенсации было необычайно большое время жизни . Оказалось, что ее время жизни почти в 1000 раз больше, чем у известных частиц такой массы. Дальнейшие исследования показали, что причиной такого долгожития является то, что в ее состав входит новый неизвестный ранее с-кварк, названный очарованным кварком. Было высказано предположение, что это мезон, состоящий из с-кварка и с-антикварка, т.е. это частица со скрытым очарованием. Так же как с s-кварком связано квантовое число s - странность, с-кварк несет новое квантовое число c, названное "очарованием". Очарованный кварк должен порождать новое семейство адронов, имеющих в своем составе с-кварк или с-антикварк. Все эти частицы тяжелые, т.к. масса очарованного кварка больше массы странного кварка. Итак кварков стало 4, но на этом открытие новых кварков не завершилось.

В 1977 году были открыты нейтральные мезоны с массами около 10 ГэВ. Они получили название ипсилон-мезонов. Так же как и -мезоны они наблюдались в реакции образования мюонных пар в протон-ядерных столкновениях и на электронно-позитронных коллайдерах и также как -мезоны они долго живущие (ширина распада -мезона 53 кэВ). Это означало открытие пятого кварка b (от beauty). В состав -мезона входят b-кварк и b-антикварк и он обладает скрытой красотой.

После почти двадцатилетних поисков, в 1995 году был открыт шестой, самый "тяжелый" кварк - t-кварк.

Таким образом, на этом этапе развития наших представлений о структуре материи на первый план выходят "новые элементарные частицы" - кварки. Все адроны состоят из шести кварков и есть достаточно серьезные основания считать, что их не должно быть больше.Квантовые числа кварков приведены в таблице 2.

Каждый тип кварка имеет еще одно квантовое число - цвет, которое может принимать три значения - красный, синий и зеленый.Это чисто условные названия. Главное, что каждый кварк имеет еще три дополнительных квантовых числа. Гипотеза о существовании цвета у кварков, впервые высказанная в 1965 году независимо Н. Боголюбовым, Б. Струминским, А. Тавхелидзе и М. Ханом, Й. Намбу, была впоследствии подтверждена в большом количестве экспериментов. Существует цветовая симметрия сильных взаимодействий. Сильное взаимодействие кварка не зависит от его цветового состояния, т.е. оно одинаково для всех трех цветов. Поскольку адроны состоят из кварков, то структура адронов в основном определяется сильным и электромагнитным взаимодействием кварков.

Основные положения составной модели адронов - модели кварков:

все сильновзаимодействующие частицы состоят из кварков; кварки являются фермионами; по современным представлениям они бесструктурны;

кварки имеют внутренние квантовые числа: электрический заряд Q, спин 1/2, четность P, барионное число B, изоспин I, проекцию изоспина I3, странность s, шарм c, bottomness b, topness t (совокупность этих внутренних квантовых чисел, характеризующих определенный тип кварка, называется также "ароматом" кварка), цвет;

квантовые числа кварков определяют характеристики адронов;

барионы (фермионы с барионным числом B = 1) строятся из трех кварков;

антибарионы (фермионы с барионным числом B = -1) строятся из трех антикварков;

мезоны (бозоны с барионным числом B = 0) строятся из кварка и антикварка;

число цветов кварков равно трем - красный, зеленый, синий;

известные барионы и мезоны - бесцветны;

кварки в адронах связаны глюонами;

кварки участвуют в электромагнитных взаимодействиях, излучая или поглощая -квант, при этом не изменяется ни цвет, ни тип (аромат) кварков

Вершина электромагнитного взаимодействия кварков;

кварки участвуют в слабых взаимодействиях, излучая или поглощая или Z-бозоны, при этом может изменяться тип (аромат) кварка, но цвет кварка при этом остается без изменения

Вершины слабого взаимодействия кварков;

кварки участвуют в сильных взаимодействиях, излучая или поглощая глюон g, при этом изменяется цвет кварка, а его тип (аромат) остается неизменным

Вершина сильного взаимодействия кварков;

каждому адрону приписывается определенная внутренняя четность. Внутреннюю четность адрона легко получить, воспользовавшись следующими правилами:

Правило 1. Четность кварка равна +1 и не зависит от типа кварка.

Правило 2. Четность антикварка равна -1 и не зависит от типа кварка.

Правило 3. Внутренняя четность адрона равна произведению четностей входящих в его состав кварков, умноженному на , где L-орбитальные моменты кварков в составе адрона, т.е. совершенно аналогично тому, как получается четность состояний в модели оболочек для системы нуклонов.

Кварковая модель позволяет качественно описать структуру адронов, получить их квантовые числа. Особое место занимают мезоны для которых кварковая модель позволяет количественно рассчитать спектры масс. Это семейства мезонов, состоящие из тяжелых кварков - чармоний (c) и боттомоний (b). Спектры их подобны спектрам водородоподобных атомов. Изучение подобных систем (кваркония) позволяет получить важную информацию о природе сильного взаимодействия.

На рис. 16 показана система уровней чармония и переходы между ними. Характерный масштаб возбуждения составляет сотни МэВ, что существенно меньше массы с-кварка. Следовательно, можно воспользоваться тем, что движение нерелятивистское и для описания кваркония использовать уравнение Шредингера. В таком подходе кварконий можно рассматривать как систему двух кварков, движущихся в потенциале V(r). Состояния кваркония и волновые функции определяются как решения станционарного уравнения Шредингера.

Рис. 16 Система уровней чармония и переходы между состояниями

Для описания спектроскопии кваркония удалось найти простой потенциал V(r). На малых расстояниях (r << 10-13 см) потенциал, аналогично кулоновскому имеет вид V(r) ~ 1/r. Поскольку кварки не наблюдаются в свободном состоянии, потенциал должен их эффективно "запирать" на расстояниях масштаба радиуса адрона (~10-13 см), т.е. на больших расстояниях потенциал должен расти (V(r) ~ r). Потенциал имеет вид

,

где , , - константы. Константы удалось подобрать так, что потенциал одновременно хорошо описывает спектры масс как (c), так и (b).

Частицы, которые связывают между собой кварки в адроны, были названы глюонами. Глюоны являются квантами сильного поля. Глюоны являются бозонами и имеют спин 1. Однако в отличие от фотонов, для того чтобы быть переносчиками цветового взаимодействия они должны обладать цветом и антицветом. Число различных типов глюонов 8, так как одна цветовая комбинация является бесцветной, т.е. не имеет цветового заряда. По аналогии с квантовой электродинамикой теория взаимодействия цветных объектов была названа квантовой хромодинамикой. Взаимодействие между кварками путем обмена глюонами является истинно сильным взаимодействием. В отличие от фотонов, которые электрически нейтральны, глюоны имеют цветовой заряд, поэтому должны сами испускать и поглощать глюоны. Это приводит к принципиально новому поведению системы кварков и глюонов. При увеличении расстояния между кварками и глюонами их энергия взаимодействия возрастает. В результате не наблюдается свободных кварков и глюонов; они "заперты" внутри бесцветных адронов (конфайнмент). Ядерное взаимодействие между нуклонами является производным от истинно сильного взаимодействия, по аналогии с силами Ван-дер-Ваальса, связывающими атомы в молекулы и являющимися производными от истинно электромагнитных взаимодействий, действующих между заряженными частицами.