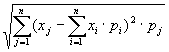- •Оглавление
- •1.Основные понятия теории множеств
- •2.Основные операции над множествами. Диаграммы Эйлера-Венна
- •3.Бинарные отношения
- •4.Перестановки
- •5.Основные операции над множествами
- •6.Декартово произведение множеств
- •7.Числовые множества. Принадлежность
- •8.Высказывания. Основные операции над высказываниями
- •9.Теоремы умножения вероятностей
- •10.Дискретные случайные величины
- •11.Нормальный закон распределения вероятностей
- •12.Основные понятия теории вероятностей
- •13.Свойства вероятностей
- •14.Элементы теории вероятностей. Математика случайного
- •15.Статистическое распределение выборки
- •16.Закон распределения вероятностей
- •17.Характеристики вариационного ряда. Мода
- •18.Характеристики вариационного ряда. Медиана
- •19.Основные понятия математической статистики
- •20.Характеристики вариационного ряда. Среднее выборочное
- •21.Языки программирования высокого уровня
- •22.Словесные алгоритмы
- •23.Блок-схемы. Ветвление
- •24.Блок-схемы. Циклы
9.Теоремы умножения вероятностей
N° [orig] |
Кол-во верных ответов: |
Вопрос: |
Варианты ответов |
1 [0] |
1 |
Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет четное число очков, равна … |
1 )
2 )
3 )
4 )
5 ) 1 |
2 [1] |
1 |
Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет четное число очков, большее 4, равна … |
1 )
2 )
3 ) 1
4 )
5 ) |
3 [3] |
1 |
Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет четное число очков, меньшее 4, равна … |
1 )
2 )
3 )
4 ) 1
5 ) |
4 [4] |
1 |
Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет четное число очков, не меньшее 4, равна … |
1 )
2 )
3 ) 1
4 )
5 ) |
5 [6] |
1 |
Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет четное число очков, не меньшее 6, равна … |
1 )
2 )
3 )
4 )
5 ) 1 |
6 [8] |
1 |
Игральный кубик бросают два раза. Вероятность того, что на верхней грани два раза выпадет нечетное число очков, большее 4, равна … |
1 )
2 ) 1
3 )
4 )
5 ) |
10.Дискретные случайные величины
N° [orig] |
Кол-во верных ответов: |
Вопрос: |
Варианты ответов |
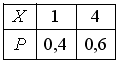
1 [0] |
1 |
Дискретная
случайная величина Х
имеет закон распределения
вероятностей:
|
1 ) 5
2 ) 1
3 ) 2,2
4 ) 2,8 |
2 [2] |
1 |
Дискретная
случайная величина Х
имеет закон распределения
вероятностей:
|
1 ) 2,6
2 ) 7
3 ) 1
4 ) 4,4 |
3 [3] |
1 |
Дискретная
случайная величина Х
имеет закон распределения
вероятностей:
|
1 ) 4,8
2 ) 8
3 ) 1
4 ) 3,2 |
4 [9] |
1 |
Дискретная
случайная величина Х
имеет закон распределения
вероятностей:
|
1 ) 1
2 ) 5
3 ) 2,3
4 ) 2,7 |
5 [12] |
1 |
Дискретная
случайная величина Х
имеет закон распределения
вероятностей:
|
1 ) 3,8
2 ) 3,2
3 ) 1
4 ) 7 |
6 [22] |
1 |
Для вычисления вероятности наступления случайного события используется формула… |
1 )
2 )
3 )
4 ) |

 Математическое
ожидание М(Х)
этой случайной величины равно...
Математическое
ожидание М(Х)
этой случайной величины равно...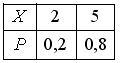 Математическое
ожидание М(Х)
этой случайной величины равно...
Математическое
ожидание М(Х)
этой случайной величины равно...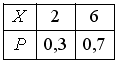 Математическое
ожидание М(Х)
этой случайной величины равно...
Математическое
ожидание М(Х)
этой случайной величины равно...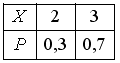 Математическое
ожидание М(Х)
этой случайной величины равно...
Математическое
ожидание М(Х)
этой случайной величины равно...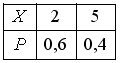 Математическое
ожидание М(Х)
этой случайной величины равно...
Математическое
ожидание М(Х)
этой случайной величины равно...