
- •Оглавление
- •Вычисление определителей
- •Матрицы: основные понятия и определения
- •Линейные операции над матрицами
- •Умножение матриц
- •Обратная матрица
- •Собственные значения матрицы
- •Системы линейных уравнений: основные понятия
- •Квадратичные формы
- •Функции: основные понятия и определения
- •Непрерывность функции. Точки разрыва
- •Производные первого порядка
- •Производные высших порядков
- •Асимптоты графика функции
- •Основные методы интегрирования
- •Свойства определенного интеграла
- •Приложения определенного интеграла
- •Основные понятия теории вероятностей
- •Теоремы сложения и умножения вероятностей
- •Полная вероятность. Формула Байеса
- •Дискретная случайная величина
- •Характеристики вариационного ряда
- •Точечные оценки параметров распределения
- •Элементы корреляционного анализа
- •Проверка статистических гипотез
- •Линейное программирование
- •Транспортная задача
- •Нелинейное программирование
- •Динамическое программирование
- •Функции полезности
- •Функции спроса и предложения
- •Производственные функции
- •Кривые безразличия
Собственные значения матрицы
N° [orig] |
Кол-во верных ответов: |
Вопрос: |
Варианты ответов |
1 [0] |
1 |
Собственные
значения собственных векторов
линейного преобразования, заданного
в некотором базисе матрицей
|
1 )
2 )
3 )
4 ) |
2 [14] |
1 |
Вектор
|
1 )
2 )
3 )
4 ) |
3 [23] |
1 |
Вектор
|
1 ) 4
2 ) − 3
3 ) 1
4 ) 1 |
4 [26] |
1 |
Вектор
|
1 ) 1
2 ) 5
3 ) 2
4 ) 2 |
5 [30] |
1 |
Вектор
|
1 ) 5
2 ) 0
3 ) 1
4 ) 5 |
6 [32] |
1 |
Вектор
|
1 ) 1
2 ) 5
3 ) 6
4 ) 6 |
Системы линейных уравнений: основные понятия
N° [orig] |
Кол-во верных ответов: |
Вопрос: |
Варианты ответов |
1 [0] |
1 |
В
системе уравнений
|
1 )
2 )
3 )
4 ) , , |
2 [4] |
1 |
В
системе уравнений
|
1 ) , ,
2 )
3 )
4 ) |
3 [5] |
1 |
В
системе уравнений
|
1 ) , ,
2 )
3 )
4 ) , , , , |
4 [7] |
1 |
В
системе уравнений |
1 ) , ,
2 ) , , , ,
3 ) ,
4 ) |
5 [8] |
1 |
В
системе уравнений |
1 )
2 ) ,
3 ) , ,
4 ) , |
6 [9] |
1 |
В
системе уравнений |
1 ) , ,
2 ) ,
3 )
4 ) |

 ,
могут быть найдены по формуле…
,
могут быть найдены по формуле…


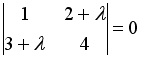
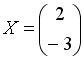 является
собственным вектором матрицы А,
соответствующий собственному значению
является
собственным вектором матрицы А,
соответствующий собственному значению
 является
собственным вектором матрицы
является
собственным вектором матрицы
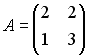 .
Тогда соответствующее собственное
значение равно …
.
Тогда соответствующее собственное
значение равно … является
собственным вектором матрицы
является
собственным вектором матрицы
 .
Тогда соответствующее собственное
значение равно …
.
Тогда соответствующее собственное
значение равно … является
собственным вектором матрицы
является
собственным вектором матрицы
 .
Тогда соответствующее собственное
значение равно …
.
Тогда соответствующее собственное
значение равно … является
собственным вектором матрицы
является
собственным вектором матрицы
 .
Тогда соответствующее собственное
значение равно …
.
Тогда соответствующее собственное
значение равно …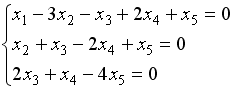 независимыми
(свободными) переменными можно считать…
независимыми
(свободными) переменными можно считать… независимыми
(свободными) переменными можно считать…
независимыми
(свободными) переменными можно считать… независимыми
(свободными) переменными можно считать…
независимыми
(свободными) переменными можно считать…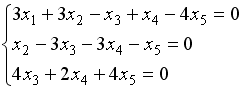 базисными
(несвободными) переменными можно
считать…
базисными
(несвободными) переменными можно
считать…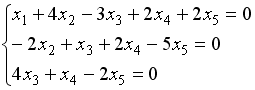 базисными
(несвободными) переменными можно
считать…
базисными
(несвободными) переменными можно
считать… базисными
(несвободными) переменными можно
считать…
базисными
(несвободными) переменными можно
считать…