
- •Оглавление
- •1.Вычисление определителей
- •2.Линейные операции над матрицами
- •3.Умножение матриц
- •4.Системы линейных уравнений: основные понятия
- •5.Основные задачи аналитической геометрии на плоскости
- •6.Прямая на плоскости
- •7.Кривые второго порядка
- •8.Прямая и плоскость в пространстве
- •9.Функции: основные понятия и определения
- •10.Предел функции
- •11.Геометрический и физический смысл производной
- •12.Производные высших порядков
- •13.Числовые последовательности
- •14.Сходимость числовых рядов
- •15.Типы дифференциальных уравнений
- •16.Дифференциальные уравнения первого порядка
- •17.Линейные дифференциальные уравнения 2 порядка
- •18.Основные понятия теории вероятностей
- •19.Теоремы сложения и умножения вероятностей
- •20.Полная вероятность. Формула Байеса
- •21.Непрерывная случайная величина
- •22.Статистическое распределение выборки
- •23.Точечные оценки параметров распределения
- •24.Интервальные оценки параметров распределения
- •25.Проверка статистических гипотез
- •26.Теория игр: матричные игры
- •27.Сетевое планирование и управление
- •28.Линейное программирование
- •29.Транспортная задача
- •30.Функции полезности
- •31.Кривые безразличия
- •32.Функции спроса и предложения
- •33.Производственные функции
22.Статистическое распределение выборки
N° [orig] |
Кол-во верных ответов: |
Вопрос: |
Варианты ответов |
1 [0] |
1 |
Из
генеральной совокупности извлечена
выборка объема n=50,
полигон частот которой имеет вид
|
1 ) 14
2 ) 16
3 ) 15
4 ) 50 |
2 [2] |
1 |
Из
генеральной совокупности извлечена
выборка объема n=40,
полигон частот которой имеет вид
|
1 ) 11
2 ) 10
3 ) 40
4 ) 12 |
3 [3] |
1 |
Из
генеральной совокупности извлечена
выборка объема n=70,
полигон частот которой имеет вид
|
1 ) 7
2 ) 70
3 ) 8
4 ) 6 |
4 [7] |
1 |
Из
генеральной совокупности извлечена
выборка объема
|
1 ) 50
2 ) 12
3 ) 10
4 ) 11 |
5 [9] |
1 |
Из
генеральной совокупности извлечена
выборка объема
|
1 ) 12
2 ) 13
3 ) 52
4 ) 14 |
6 [10] |
1 |
Из
генеральной совокупности извлечена
выборка объема
|
1 ) 14
2 ) 53
3 ) 15
4 ) 13 |
23.Точечные оценки параметров распределения
N° [orig] |
Кол-во верных ответов: |
Вопрос: |
Варианты ответов |
1 [0] |
1 |
Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 5, 6, 9, 12. Тогда несмещенная оценка математического ожидания равна… |
1 ) 8,5
2 ) 8
3 ) 7
4 ) 8,25 |
2 [2] |
1 |
Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 4, 7, 8, 9. Тогда несмещенная оценка математического ожидания равна… |
1 ) 7,25
2 ) 6,5
3 ) 7
4 ) 6 |
3 [3] |
1 |
Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 3, 8, 9, 16. Тогда несмещенная оценка математического ожидания равна… |
1 ) 8
2 ) 9,5
3 ) 9,25
4 ) 9 |
4 [7] |
1 |
Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 4, 5, 6, 9. Тогда несмещенная оценка математического ожидания равна… |
1 ) 5
2 ) 6,5
3 ) 6
4 ) 5,75 |
5 [9] |
1 |
Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 2, 3, 7, 9. Тогда несмещенная оценка математического ожидания равна… |
1 ) 5
2 ) 6
3 ) 5,25
4 ) 5,5 |
6 [10] |
1 |
Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 2, 3, 6, 9. Тогда несмещенная оценка математического ожидания равна… |
1 ) 6
2 ) 5
3 ) 5,25
4 ) 5,5 |

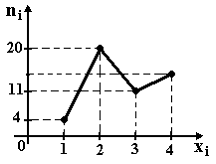 Тогда
число вариант xi=4
в выборке равно…
Тогда
число вариант xi=4
в выборке равно…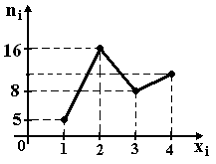 Тогда
число вариант xi=4
в выборке равно…
Тогда
число вариант xi=4
в выборке равно…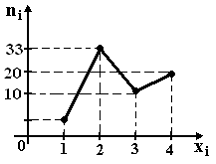 Тогда
число вариант xi=1
в выборке равно…
Тогда
число вариант xi=1
в выборке равно…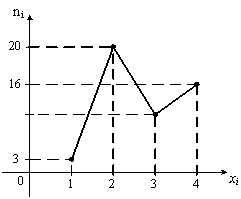 Тогда
число вариант
Тогда
число вариант
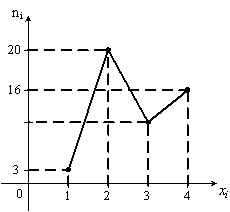 Тогда
число вариант
в выборке равно…
Тогда
число вариант
в выборке равно…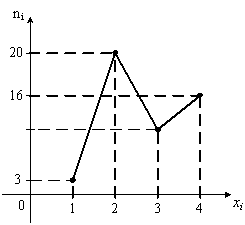 Тогда
число вариант
в
выборке равно…
Тогда
число вариант
в
выборке равно…