2. Системы физических величин

Система физических величин (система величин) - совокупность физических величин, образованная в соответствии с принятыми принципами, когда одни величины принимают за независимые (основные), а другие определяют как функции независимых величин (производные).

В названии системы величин применяют символы величин, принятых за основные. Так система величин механики, в которой в качестве основных приняты длина L, масса М и время Т, должна называться системой LMT. Система основных величин, соответствующая Международной системе единиц (СИ), должна обозначаться символами LMTIQNJ, обозначающими соответственно символы основных величин - длины L, массы М, времени Т, силы электрического тока I, температуры Q, количества вещества N и силы света J.

Основная физическая величина (основная величина) - физическая величина, входящая в систему величин и условно принятая в качестве независимой от других величин этой системы

Производная физическая величина (производная величина) - физическая величина, входящая в систему величин и определяемая через основные величины этой системы.

Примеры:

- скорость V поступательного движения, определяется (по модулю) уравнением , где l - путь, t - время;

- сила F, приложенная к материальной точке, определяется (по модулю) уравнением , где т - масса точки, а - ускорение, вызванное действием силы F.

Формализованным отражением качественного различия между измеряемыми физическими величинами служит их размерность.

Размерность физической величины - выражение в форме степенного одночлена, составленного из произведений символов основных физических величин в различных степенях и отражающее связь данной физической величины с физическими величинами, принятыми в данной системе за основные с коэффициентом пропорциональности, равным единице.

В соответствии с международным стандартом ИСО 31/0, размерность величин следует обозначать знаком dim (от слова dimension). В системе величин LMT размерность величины x будет:

где L, M, T - символы величин, принятых за основные (соответственно длины, массы, времени); l, т, t - показатели размерности.

Степени символов основных величин, входящих в одночлен, в зависимости от связи рассматриваемой производной физической величины с основными, могут быть целыми, дробными, положительными, отрицательными, нулем. Понятие размерность распространяется и на основные величины. Размерность основной величины в отношении самой себя равна единице, т.е. формула размерности основной величины совпадает с ее символом.

Если все показатели размерности равны нулю, то такую величину называют безразмерной. Она может быть:

- относительной, определяемой как отношение одноимённых величин (например, относительная диэлектрическая проницаемость);

- логарифмической, определяемой как логарифм относительной величины (например, логарифм отношения мощностей или напряжений).

Безразмерная величина в одной системе величин может быть размерной в другой системе.

Пример - Электрическая постоянная Е_о в электростатической системе является безразмерной величиной, а в системе величин СИ имеет размерность

При определении размерности производных физических величин руководствуются следующими правилами:

1. размерности левой и правой частей уравнения равны между собой;

2. алгебра размерностей мультипликативна, т.е. состоит всего лишь из двух действий - умножения и деления;

3. размерность произведения нескольких величин равна произведению их размерностей. Так, если зависимость между величинами имеет вид 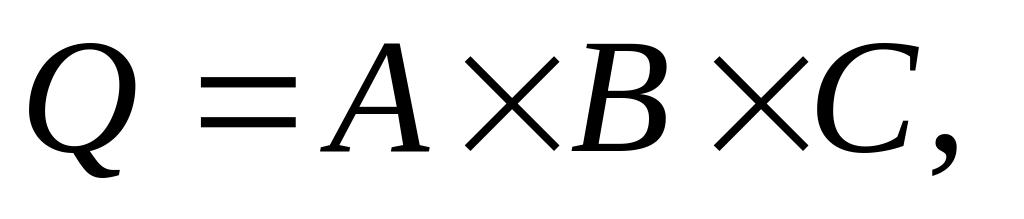то

4. размерность частного при делении одной величины на другую равна отношению их размерностей, т.е. если 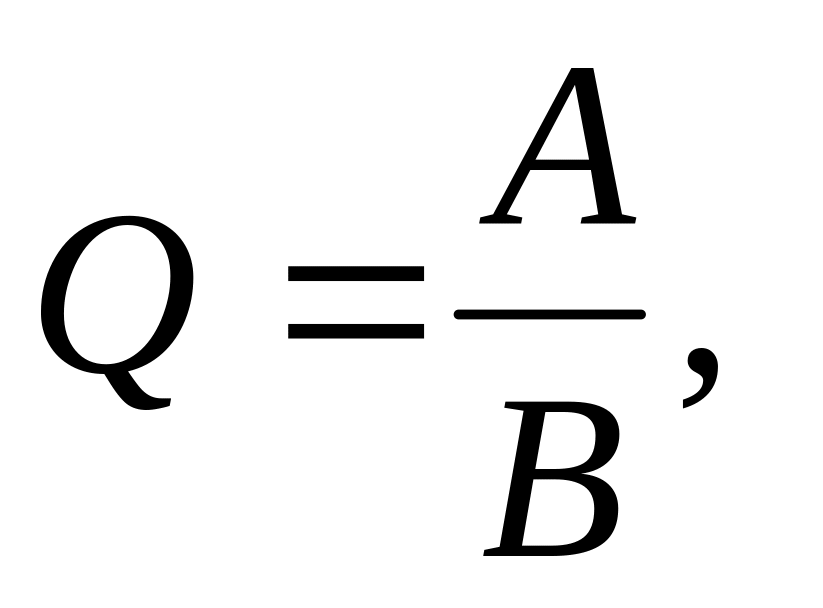то

5. размерность любой величины, возведенной в степень, равна её размерности в той же степени. Так, если 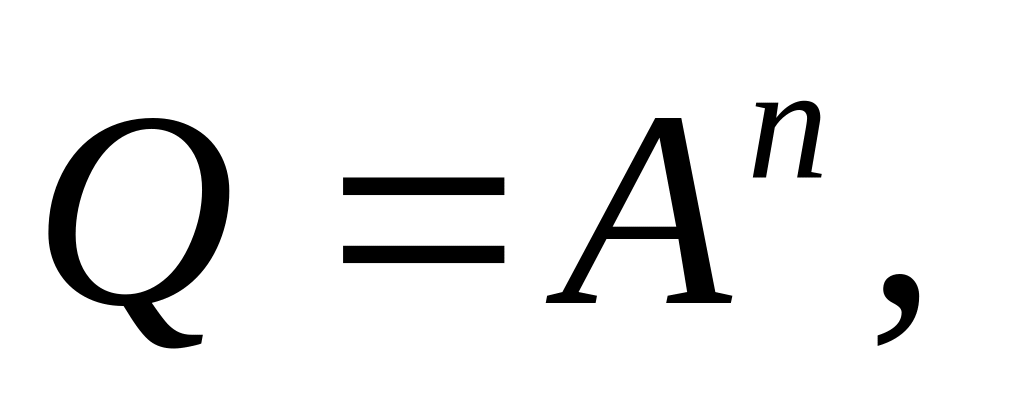то

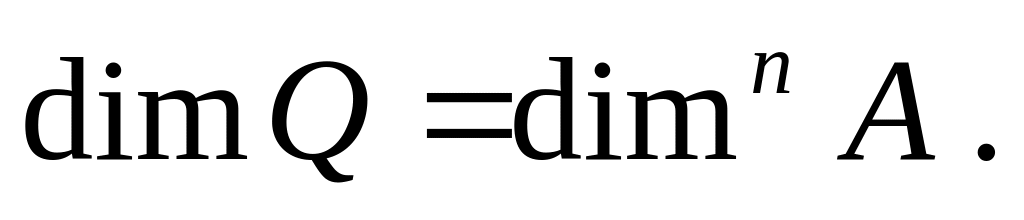
Итак, размерность является качественной характеристикой измеряемой величины. Она отображает ее связь с основными величинами и зависит от их выбора. Как указывал М. Планк, вопрос об «истинной» размерности любой величины «имеет не больше смысла, чем вопрос об «истинном названии какого-либо предмета». По этой причине в гуманитарных науках, искусстве, квалиметрии, где номенклатура основных величин не определена, теория размерностей не находит эффективного применения. В физике, напротив, методами теории размерности нередко удается получить важные самостоятельные результаты. Формальное применение алгебры размерностей иногда позволяет определить неизвестную зависимость между физическими величинами.

Пример - В результате измерений установлено, что при движении по окружности сила F, прижимающая тело к опоре, в какой-то степени зависит от скорости V, массы m и радиуса окружности r:

F =V^a m^b r^c.

Каков вид этой зависимости?

Решение: На основании алгебры размерностей

dim F = dim^aV dim^b m dim^c r,

но dim F = LMT^-2; dim m = M; dim V = LT^-1; dim r = L .

Отсюда

LMT^-2= (LT^-1)^a M^b L^c = L^a+c M^b T^-a.

Приравнивая показатели степени при одноименных переменных, имеем

a+c=1; b=1; -a= -2.

И тогда a=2; b=1; с= -1.

Таким образом, исследуемая зависимость имеет вид .

Теория размерностей повсеместно применяется для определения проверки правильности сложных формул. Если размерности левой и правой частей не совпадают, то в выводе формулы, к какой бы области знаний она ни относилась, следует искать ошибку.