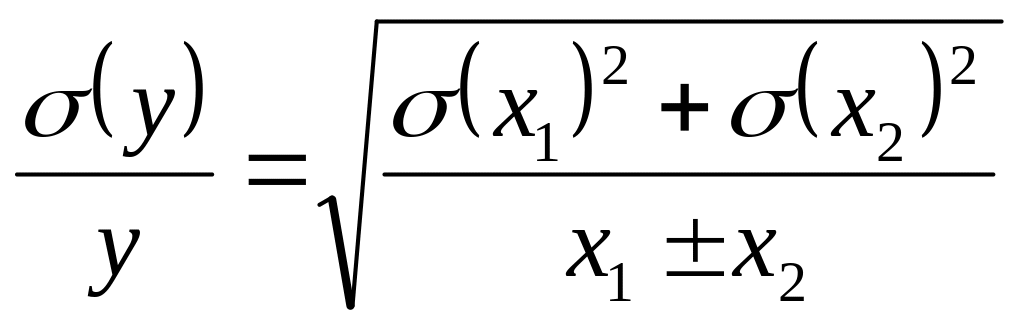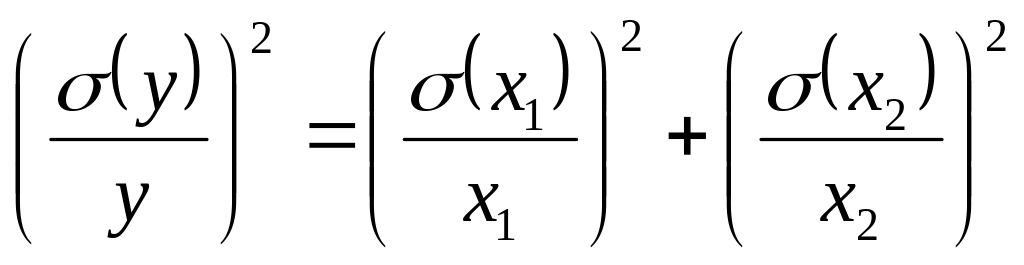- •Часть 1. Основы метрологии
- •Содержание
- •5.10 Контрольные вопросы к разделу 5 132
- •1 Общие сведения о физических величинах
- •Физические величины
- •Системы физических величин
- •1.3 Единицы физических величин
- •1.4 Измерительные шкалы
- •1.4.1 Шкала физической величины
- •1.4.2 Неметрические шкалы
- •1.4.3 Метрические шкалы
- •1.5 Контрольные вопросы к разделу 1
- •1.6 Тестовые вопросы по тематике раздела 1
- •Тема 1 – Введение в метрологию
- •Тема 2 - Физические величины
- •Тема 3 - Системы единиц физических величин
- •Тема 4 - Шкалы измерений
- •2 Методы и средства измерений физических величин
- •2.1 Измерения физических величин
- •2.2 Классификация измерений
- •2.3 Средства измерений и их классификация
- •2.4 Устройство средств измерений, принцип их работы
- •2.5 Эксплуатационные характеристики средств измерений
- •2.6 Критерии качества измерений
- •2.7 Результаты измерения физических величин
- •2.8 Условия измерений
- •2.9 Контрольные вопросы к разделу 2
- •2.10 Тестовые вопросы по тематике раздела 2
- •Тема 1 – Измерения физических величин
- •Тема 2 - Классификация измерений
- •Тема 3 - Общие сведения о средствах измерений
- •3 Погрешности средств измерений
- •3.1 Классификация погрешностей средств измерений
- •3.2 Классы точности средств измерений
- •3.3 Систематические погрешности
- •3.3.1 Классификация систематических погрешностей
- •3.3.2 Методы борьбы с систематическими погрешностями
- •3.4 Случайные погрешности
- •Погрешности косвенных измерений
- •3.6 Контрольные вопросы к разделу 3
- •3.7 Тестовые вопросы по тематике раздела 3
- •Тема 1 - Погрешности измерений, их классификация
- •Тема 2 – Выбор средства измерений по точности
- •Тема 3 – Обработка результатов однократных измерений
- •Тема 4 – Обработка результатов многократных измерений
- •4 Обработка результатов измерений
- •4.1 Обработка результатов прямых точечных измерений
- •4.1.1 Алгоритм обработки результатов прямых многократных
- •4.1.2 Результат измерения и оценка его среднего квадратического
- •4.1.3 Проверка нормальности результатов наблюдений
- •4.1.4 Доверительные границы случайной погрешности
- •4.1.5 Доверительные границы неисключенной систематической
- •4.1.6 Граница погрешности результата измерения
- •4.1.7 Форма записи результатов измерений
- •Правила округления результатов измерения
- •Погрешность результата измерения округляется до двух значащих цифр, если первая из них - 1 или 2 и до одной значащей цифры, если она равна 3 и более;
- •Результат измерения округляется до того же десятичного разряда, которым оканчивается округлённое значение погрешности;
- •Округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одной - двумя запасными значащими цифрами.
- •4.2 Расчёт метрологических характеристик средств измерений
- •Общие положения
- •Общие методы оценки и контроля индивидуальных
- •Методики ориентировочной оценки метрологических и
- •4.2.4 Метод нименьших квадратов
- •4.2.5 Алгоритмы обработки результатов наблюдений
- •4.3 Контрольные вопросы к разделу 4
- •4.4 Тестовые вопросы по тематике раздела 4
- •Тема 1 - Форма записи результатов измерений
- •5 Обеспечение единства измерений
- •5.1 Общие положения
- •5.2 Эталоны единиц физических величин
- •5.3 Метрологические службы
- •5.3.1 Государственная метрологическая служба и иные
- •5.3.2 Метрологические службы государственных органов
- •5.4 Государственный метрологический контроль и надзор
- •5.5 Утверждение типа средств измерений
- •5.6 Передача информации о размерах единиц
- •5.7 Поверка и калибровка средств измерений
- •5.8 Методы поверки и калибровки, поверочные схемы
- •5.9 Права и обязанности государственных инспекторов
- •5.9.1 Государственный метрологический контроль и надзор
- •5.9.2 Права государственных инспекторов, осуществляющих
- •5.9.3 Права инспекторов в случае нарушений
- •5.9.4 Ответственность государственных инспекторов
- •5.10 Контрольные вопросы к разделу 5
- •5.11 Тестовые вопросы по тематике раздела 5
- •Тема 1 – Обеспечение единства измерений. Общие положения
- •Тема 2 – Эталоны единиц фв. Передача информации о размерах единиц
- •Тема 3 – Метрологические службы
- •Тема 4 – Поверка и калибровка средства измерения. Поверочные схемы
- •Тема 5 – Государственный метрологический контроль и надзор
- •Борис Моисеевич Кербель Ирина Геннадьевна Попова Метрология, стандартизация, сертификация
- •Часть 1. Основы метрологии
- •636036, Томская обл., г. Северск,
Погрешности косвенных измерений
При
косвенных измерениях измеряемая величина
![]() ,
функционально связана с одной или
несколькими непосредственно измеряемыми
величинами
,
функционально связана с одной или
несколькими непосредственно измеряемыми
величинами
![]() .
.
Рассмотрим
простейший случай определения ошибки
одной переменной, когда
![]() .
Имеем
.
Имеем
![]() .
.
Разложив правую часть этого равенства в ряд Тейлора и пренебрегая членами разложения, содержащими в степени выше первой, получим выражение абсолютной погрешности
![]() или
или
![]() . (3.40)
. (3.40)
Относительная ошибка измерения функции определится из выражения
![]() . (3.41)
. (3.41)
Если измеряемая величина Y является функцией нескольких переменных Y= f( ), то абсолютная погрешность результата косвенных измерений будет равна
![]() ,
(3.42)
,
(3.42)
где
![]() ,
,
![]() ,
,
![]() - частные производные от Y
по
;
- частные производные от Y
по
;
![]() и т.д. – средние квадратические отклонения
результатов прямых измерений величин
.
и т.д. – средние квадратические отклонения
результатов прямых измерений величин
.
Относительная погрешность результата косвенных измерений равна
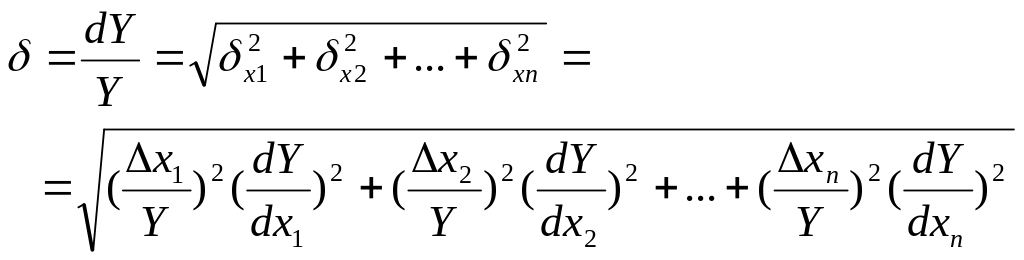 .
(3.43)
.
(3.43)
Пример
- Пусть параметр
![]() функционально связан с измеряемыми
параметрами зависимостью
функционально связан с измеряемыми
параметрами зависимостью
![]() .
.
Применив формулу (3.42), имеем
![]()
или в относительной форме
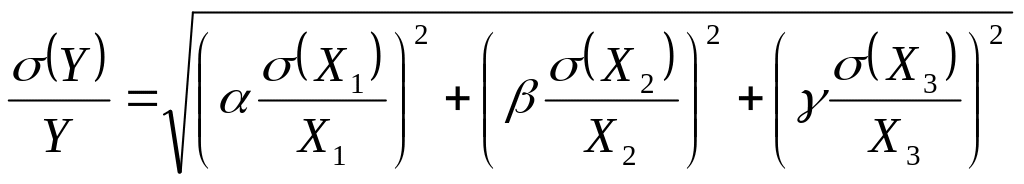 .
(3.44)
.
(3.44)
В большинстве практических случаев мы имеем дело с косвенными измерениями, в которых участвуют только два прямых измерения. Согласно теории вероятностей среднее квадратическое значение отклонения суммы двух величин от её математического ожидания вычисляется по формуле
![]() , (3.45)
, (3.45)
где
![]() - коэффициент корреляции.
- коэффициент корреляции.
По степени коррелированности погрешности обычно подразделяют на два вида:
cильнокоррелированные
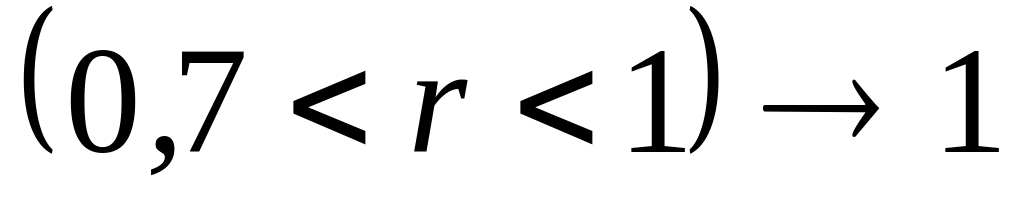 ,
,cлабокоррелированные
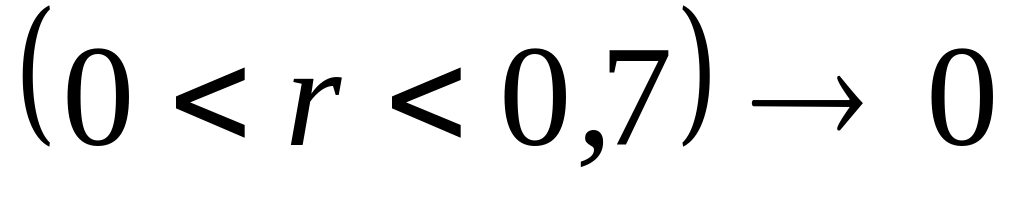 .
.
Тогда из (3.44) для сильнокорелированных величин имеем
![]() , (3.46)
, (3.46)
для слабокоррелированных
![]() . (3.47)
. (3.47)
Погрешность
![]() измерительной системы, состоящей из
измерительной системы, состоящей из
![]() последовательно соединённых приборов
(или преобразователей), необходимо
рассматривать как ряд независимых
случайных погрешностей и вычислять на
основании вышеприведённой формулы для
слабокоррелированных (независимых)
погрешностей.
последовательно соединённых приборов
(или преобразователей), необходимо
рассматривать как ряд независимых
случайных погрешностей и вычислять на
основании вышеприведённой формулы для
слабокоррелированных (независимых)
погрешностей.
Формулы для вычисления абсолютных и относительных погрешностей измерения некоторых, наиболее часто встречающихся в измерительной технике, функций приведены в таблице 3.4.
Таблица 3.4 – Формулы для вычисления погрешностей косвенных измерений
Функциональная
связь
|
Соотношение между среднеквадратическими ошибками |
|
|
|
|
|
|
|
|
|
|
Пример
- Пусть
![]() .
.
Значение
абсолютной погрешности равно
![]() или в относительной форме
или в относительной форме
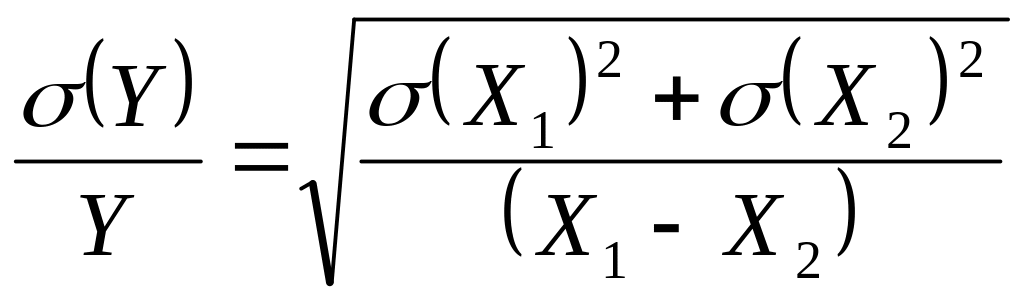 .
.
3.6 Контрольные вопросы к разделу 3
1) Дайте определение погрешности средства измерения.
2) Как классифицируются погрешности средств измерений?
3) Назовите виды погрешностей.
4) Перечислите погрешности средств измерений по форме числового выражения.
5) Дайте определение термину «инструментальная погрешность»?
6) Поясните, что такое класс точности СИ.
7) Является ли класс точности СИ непосредственной оценкой точности измерений, выполняемых этим СИ?
8) Может ли средство измерения иметь несколько классов точности?
9) Каким образом можно свести влияние систематической погрешности к минимуму?
10) Какая погрешность обусловлена особенностями оператора?
11) Чем может быть обусловлена погрешность метода измерения?
12) Чем статическая погрешность отличается от динамической?
13) Что такое случайное событие?
14) Как рассчитывается среднеквадратичное отклонение?
15) Что такое доверительный интервал и доверительная вероятность?
16) Сформулируйте «правило трех сигм».
17) Опишите порядок действий при обработке небольшого объема экспериментальных данных с использованием t – распределения Стьюдента.