3.1 Классификация погрешностей средств измерений

Погрешность средства измерений - разность между показанием средства измерений и истинным (действительным) значением измеряемой физической величины.

Погрешность меры - разность между номинальным значением меры и действительным значением воспроизводимой ею величины. Поскольку истинное значение физической величины неизвестно, то на практике пользуются ее действительным значением, которое воспроизводится образцовым средством измерений или мерой. Для самой меры показанием является ее номинальное значение.

На рисунке 3.1 показана классификация погрешностей средств измерений, в которой они условно разбиты на пять групп в зависимости от природы их происхождения.

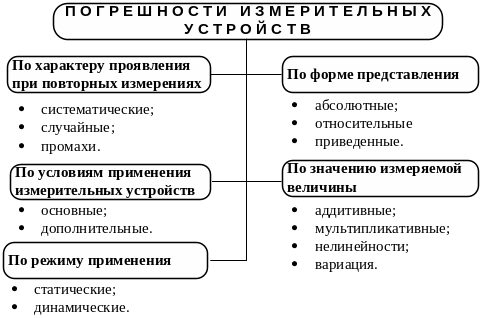
Рисунок 3.1 – Классификация погрешностей средств измерений

Систематическая погрешность средства измерений – составляющая погрешности измерения, которая при повторении равноточных измерений остаётся постоянной или закономерно изменяется. Эту погрешность можно исключить или вносить соответствующие поправки.

Систематическая погрешность конкретного средства измерений, как правило, будет отличаться от систематической погрешности другого экземпляра средства измерений этого же типа, вследствие чего для группы однотипных средств измерений систематическая погрешность может иногда рассматриваться как случайная погрешность. Причины возникновения систематических погрешностей и их классификация будут рассмотрены отдельно.

Случайная погрешность средства измерений (случайная погрешность) – составляющая погрешности измерения, которая изменяется случайным образом. случайная погрешность может быть обнаружена при повторных измерениях одной и той же величины, когда получаются неодинаковые результаты. Её нельзя исключить, но их влияние на результата измерения может быть теоретически учтено методами теории вероятности и математической статистики.

Промах - погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Иногда вместо термина «промах» применяют термин грубая погрешность измерений.

Промахи связаны с резким нарушением условий испытаний при отдельном наблюдении: толчки, неисправности измерительной аппаратуры, неправильные действия наблюдателя. Результаты измерений, содержащие промахи, должны быть отброшены как недостоверные.

Основная погрешность средства измерений (основная погрешность) - погрешность средства измерений, применяемого в нормальных условиях.

Дополнительная погрешность средства измерений (дополнительная погрешность) - составляющая погрешности средства измерений, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения или вследствие ее выхода за пределы нормальной области значений.

Статическая погрешность средства измерений (статическая погрешность) - погрешность средства измерений, применяемого при измерении физической величины, принимаемой за неизменную.

Динамическая погрешность средства измерений (динамическая погрешность) - погрешность средства измерений, возникающая при измерении изменяющейся (в процессе измерений) физической величины.

Абсолютная погрешность средства измерений (абсолютная погрешность) - погрешность средства измерений, выраженная в единицах измеряемой физической величины

 = х_изм – х_д , (3.1)

где х_изм - измеренное значение, х_д – действительное значение измеряемой величины.

Абсолютное значение погрешности - значение погрешности без учета ее знака (модуль погрешности). Необходимо различать термины абсолютная погрешность и абсолютное значение погрешности.

Относительная погрешность средства измерений (относительная погрешность) - погрешность средства измерений, выраженная отношением абсолютной погрешности средства измерений к результату измерений или к действительному значению измеренной физической величины

(3.2)

или

. (3.2*)

Приведенная погрешность средства измерения (приведенная погрешность) - относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, по-

стоянному во всем диапазоне измерений или в части диапазона

, (3.3)

где - нормирующее значение. Часто за нормирующее значение принимают верхний предел измерений.

Аддитивная погрешность (по лат. – получаемая путем сложения) – погрешность, не зависящая от измеряемой величины. По закономерности проявления аддитивные погрешности могут быть случайными или систематическими.

Случайная аддитивная погрешность, например, вызываемая трением в опорах измерительного механизма, контактными сопротивлениями, дрейфом нуля и др., при изменении измеряемой величины принимать произвольное, но не зависящее от измеряемой величины значения. Её предельные значения образуют на характеристике полосу постоянной величины (рисунок 3.2,а). Точно такая же картина будет, если погрешность представляется как приведенная, поскольку знаменатель в выражении (3.3) не изменяется на протяжении всей шкалы независимо от значения измеряемой величины.

Примером систематической аддитивной погрешности является смещение нуля характеристики аналогового средства измерения (рисунок 3.2,б).

1 - фактическая характеристика, смещенная влево на длину О-О^ ; 2 – номинальная характеристика прибора; _с – значение систематической погрешности;

⁰_пр – предельное значение случайной погрешности

Рисунок 3.2 – Смещение характеристик аналогового измерительного прибора под влиянием аддитивных систематической (а) и случайной (б) погрешностей

Мультипликативная погрешность (по лат. - получаемая путем умножения) – погрешность, величина которой изменяется прямо пропорционально измеряемой величине.

Пример - Источники мультипликативной погрешности – действие влияющих величин на параметры элементов и узлов СИ, например, изменение собственного сопротивления амперметра и встроенного в него шунта при изменении температуры окружающей среды.

В этом случае результат измерения определяется по формуле:

Поскольку при изменении температуры окружающей среды сопротивления и изменяются неодинаково, т.к. сделаны из разных материалов, погрешность измерения будет изменяться пропорционально соотношению этих сопротивлений.

Погрешность нелинейности имеет нелинейную зависимость от измеряемой величины. Чаще всего возникает как систематическая погрешность, связанная с линеаризацией номинальной статической характеристики.

Вариация имеет нелинейную зависимость от измеряемой величины, появляется вследствие гистерезисных явлений, вариации, проявляющейся при подходе к измеряемой точке со стороны меньших и больших значений; проявляется как систематическая погрешность (рисунок 3.3).

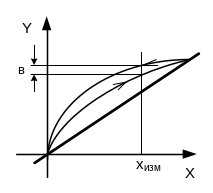
Рисунок 3.3 - Графическое представление вариации