2.4 Устройство средств измерений, принцип их работы

Средство измерения можно рассматривать как преобразователь физической величины, воспринимаемой за входной сигнал x, в другую физическую величину - выходной сигнал y, пригодную для отсчёта человеком (оператором) или удобную для дальнейшей переработки без участия человека.

Средство измерений, как правило, состоит из ряда преобразователей, в которых измерительная информация претерпевает определенные преобразования с целью получения выходного сигнала в нужной форме и нужного уровня. Все эти преобразования принято показывать на схеме, на которой показаны в виде условных изображений или обозначений составные части (звенья) изделия и связи между ними. При этом различают:

- структурные схемы, служащие для общего ознакомления со средством измерения, его основными звеньями, их назначением и взаимосвязью; поэтому составные части изделия изображаются упрощенно в виде прямоугольников, допускается применять условные графические обозначения;

- функциональные схемы, разъясняющие определённые процессы, протекающие в отдельных функциональных звеньях, цепях изделия или в изделии в целом; этими схемами пользуются для изучения принципов работы средства измерения, а также при их наладке, контроле, ремонте.

Структурной схемой средства измерения называют его условную схему, на которой упрощенно показаны все звенья измерительной цепи и путь преобразования входной величины в выходную величину.

На рисунке 2.5 показана структурная схема средства измерения, состоящего из одного преобразователя (звена).

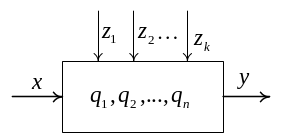
Рисунок 2.5 - Схема средства измерения, состоящего из одного звена

Входным сигналом служит измеряемая величина (давление, температура, электрический ток, электрическое напряжение и т.д.). Вид выходного сигнала зависит от способа выдачи измерительной информации, обычно в СИ это отсчетное устройство, выполненное в виде шкалы и указателя. Помимо входного и выходного сигналов на схеме обозначают внутренние параметры , присущие данному СИ, и внешние параметры , отображающие условия, в которых эксплуатируется измерительной устройство. К внутренним параметрам относятся геометрические размеры деталей звена, физические свойства материалов, из которых изготовлены детали, а также внутренние дестабилизирующие воздействия (силы трения, небаланса, температурные изменения и т.д.). Внешние параметры – это параметры окружающей среды (атмосферное давление, температура и т.д.), источников питания, внешних электрических, магнитных, гравитационных полей и т.д.

Для изучения свойств средства измерения на основе анализа его структурной схемы устанавливают его математическую модель, которая описывает связь между входным и выходным сигналами. При этом математическую модель можно представить в трех видах, в зависимости от принятых допущений о существенности влияния тех или иных параметров и их погрешностей.

Первая, и самая простая модель учитывает требуемые точные (или приписанные) показания, реализуемые средствами поверки средства измерений. В этом случае само средство измерения рассматривается как «черный ящик», взаимосвязь внутренних и внешних параметрах не рассматривается, а задается только закон построения его шкалы, т.е. задается желаемая математическая модель в виде

(2.4)

Математическую модель (2.4), при установившихся значениях входного и выходного сигналов называют также, в зависимости от цели её анализа, статической характеристикой СИ или функцией преобразования. Если математическая модель заранее определена техническим заданием при проектировании СИ, её называют заданной или номинальной статической характеристикой, при условии, что все внутренние параметры преобразователя соответствуют своим номинальным чертёжным размерам, т.е выполнены без погрешностей. В этом случае выражение (2.4) записывают в виде

(2.4^*)

Градуировочная характеристика средства измерения (градуировочная характеристика) - зависимость между значениями величин на входе и выходе средства измерений, полученная экспериментально. По своей сути эта характеристика является обратной по отношению к номинальной и её формула имеет вид

(2.5)

где значения y на входе средства измерения задают при помощи образцовых мер или СИ с присущими им погрешностями при поверке испытуемого средства измерения. Существенно, что номинальная и градуировочная характеристики близки, но не тождественны, т.к. номинальная характеристика, в отличие от градуировочной, не включает погрешности поверки, т.е. является идеальной (приписанной).

Математическая модель, учитывающая принятые метод (принцип действия) и схему средства измерения, учитывающая влияние всех внутренних и внешних параметров без учета их погрешностей, имеет вид

(2.6)

Математическую модель вида (2.6) называют также расчетной при номинальных значениях всех внутренних параметрах СИ в целом и каждого преобразователя в отдельности.

Реальная математическая модель, учитывающая погрешности параметров, возникающие либо в процессе изготовления, либо в процессе эксплуатации средства измерения может быть записана в виде:

(2.7)

где q – теоретическое значение внутреннего параметра, z – теоретическое значение внешнего параметра,  - погрешность параметра, i – текущий номер внутреннего параметра, j – текущий номер внешнего параметра, 1  i  n, 1  j  k, n – количество внутренних параметров, k - количество внешних параметров.

На рисунке 2.6 представлено графическое изображение математических моделей, где прямая 1 соответствует номинальной статической характеристике, построенной по уравнению (2.4^*), кривая 2 соответствует расчетной (теоретической) модели, построенной по уравнению (2.6), кривая 3 показывает реальную характеристику, построенную по уравнению (2.7) . Необходимо отметить, что последняя кривая сглажена для наглядности, на самом деле она представляет собой набор точек на графике, отмечающих отдельные показания СИ при задании соответствующих входных сигналов. Переход от кривой 3 к кривой 2 и затем прямой 1 осуществляется путем математической обработки результатов измерений различными методами, например методом наименьших квадратов.

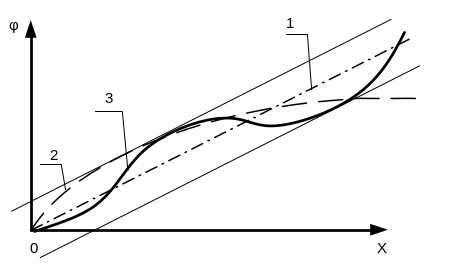
1 – номинальная статическая характеристика; 2 – теоретическая модель;

3 – реальная характеристика

Рисунок 2.6 – Графическое представление математических моделей СИ

Математическое описание СИ необходимо для выполнения различных расчетов, включая расчеты на точность и расчеты при анализе погрешностей.

Все звенья, входящие в измерительную цепочку структурной схемы, подразделяют по типовому признаку: чувствительные элементы, передаточные механизмы, отсчётные устройства, электрические преобразователи, масштабные преобразователи и т.д.

Различают два основных вида структурных схем: прямого преобразования и уравновешивающего (компенсационного) преобразования – схемы с отрицательной обратной связью.

Структурная схема средства измерения прямого преобразования показана на рисунке 2.7, где - звенья (преобразователи), - входной, - выходной, - промежуточные сигналы (информационные параметры). Как видно, входной сигнал x последовательно претерпевает несколько преобразований и, в конечном счёте, на выходе получается сигнал y.

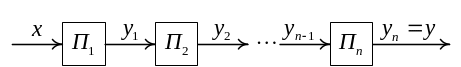
Рисунок 2.7 - Структурная схема прямого преобразования

Статическая характеристика СИ (функция преобразования) по звеньям:

.

Общая характеристика находится совместным решением системы уравнений:

. (2.8)

Примером средства измерения прямого преобразования может служить манометр для измерения давления, показанный на рисунке 2.8. Он состоит из мембранной коробки 1, преобразующей давление в линейное перемещение центра мембраны, кривошипно-шатунного механизма 2, преобразующего это линейное перемещение в угловое, рычага - указателя 3, который преобразует угловое перемещение кривошипа в линейное перемещение стрелки, находящейся на его конце и отсчетного устройства 4 – шкалы, проградуированной в единицах давления.

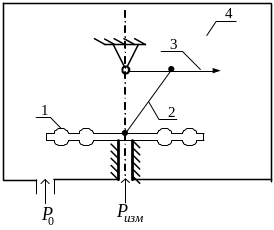
Рисунок 2.8 – Принципиальная схема манометра

Из данной схемы видно, что поступающий сигнал измерительной информации о давлении последовательно преобразуется в показание измерительного прибора, при этом все преобразования имеют свое строгое место и назначение в измерительной цепочке, целью которых является получение информации об измеряемом параметре в нужной форме и в нужном масштабе. Например, при необходимости получить сигнал в электрической форме, можно поставить между рычагом 3 и шкалой 4 дополнительный преобразователь перемещения в электрический сигнал в виде потенциометра.

Структурная схема манометра, составленная на основе принципиальной схемы, показана на рисунке 2.9.

Рисунок 2.9 – Структурная схема манометра

Структурная схема СИ уравновешивающего преобразования (с отрицательной обратной связью) имеет вид, показанный на рисунке 2.10.

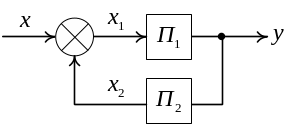
Рисунок 2.10 – Структурная схема средства измерения с обратной связью

Из данной структурной схемы видно, что Уравнение связи записывается как , где знак «-» означает отрицательную обратную связь, знак «+» - положительную обратную связь. Тогда функция преобразования имеет вид:

. (2.9)

Примером может служить средство измерения давления – манометр с силовой компенсацией, схема которого показана на рисунке 2.11. Манометр состоит из чувствительного упругого элемента (сильфона) 1, тангенсного механизма (рычага) 2, силового механизма, состоящего из двух электромагнитов 3 с якорями 4, индикатора положения 5, усилителя 6 и отсчетного устройства (ОУ) 7.

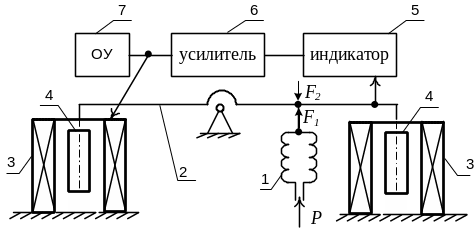
Рисунок 2.11 – Манометр с силовой компенсацией

Манометр работает следующим образом. Измеряемое давление Р поступает в сильфон 1, который преобразует давление в перемещение тангенсного (рычажного) механизма 2. Если бы манометр работал по принципу прямого преобразования, то это перемещение можно было бы сразу отправить при помощи стрелки на отсчетное устройство. Однако при этом возникает существенная нелинейность, вызванная особенностями тангенсного механизма, статическая характеристика которого заложена уже в самом его названии. Во избежание этого явления и вводится силовая компенсация, которая делает статическую характеристику манометра линейной. Перемещение тангенсного механизма фиксирует индикатор 5, который передает соответствующий сигнал на усилитель 6. Усилитель вырабатывает электрический сигнал, пропорциональный перемещению тангенсного механизма и передает его на силовой механизм, который возвращает тангенсный механизм в исходное горизонтальное положение. Сигнал, вырабатываемый при этом усилителем, служит мерой измеряемого давления. В свою очередь и сильфон в данном случае является не преобразователем давления в перемещение, а преобразователем давления в силу F₁, сосредоточенную в месте его контакта с рычагом. Силовой механизм вырабатывает силу F₂, уравновешивающую силу F_1.. В измерительной технике эту силу называют перестановочным усилием. В момент равенства этих сил рычаг 2 находится в горизонтальном положении, т.е. его перемещение равно нулю. В этом и состоит метод компенсации, при котором сигналом измерительной информации служит величина электрического тока, необходимого для создания необходимого перестановочного усилия, соответствующего измеряемому давлению. Линеаризация шкалы манометра достигается тем, что тангенсный механизм по сути дела во время всего процесса измерения остается в нейтральном (горизонтальном) положении и, вследствие этого, не вносит искажений за счет перемещения.

Структурная схема рассматриваемого манометра показана на рисунке 2.12.

Из схемы видно, что прямая и обратная цепи преобразования могут содержать не по одному звену, а по несколько последовательно соединённых звеньев. Используя выражения (2.8) и (2.9), можно вывести статическую характеристику данного средства измерения.

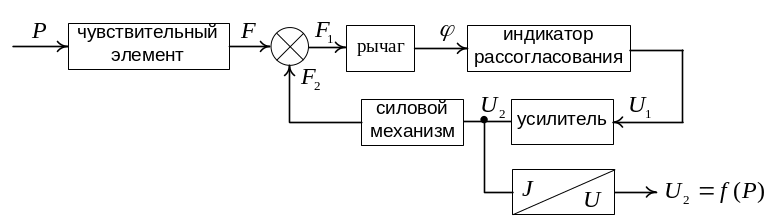
Рисунок 2.12 – Структурная схема манометра с силовой компенсацией