10. Основные характеристики переменных токов и напряжений.

Мгновенными значениями напряжений, токов и других физических величин называются соответствующие функции времени. Мгновенные значения обозначают маленькими буквами, например, 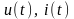, ... , или , ... .

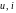Действующим значением периодического напряжения называется число

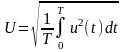, здесь и далее T – период колебаний.

Аналогично определяются действующие значения других периодических величин. Действующие значения обозначаются большими буквами.

Физический смысл действующих значений можно определить так.

Если мы подключаем резистор R к источнику переменного напряжения с действующим значением U, то в нем выделяется такая же средняя мощность, как и при подключении этого резистора к источнику постоянного напряжения U.

Если мы пропускаем через резистор R переменный ток с действующим значением I, то в нем выделяется такая же средняя мощность, как и при пропускании через него постоянного тока I.

Средним значением периодического напряжения называется число

.

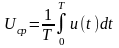Аналогично определяются средние значения других периодических величин. Среднее значение периодической физической величины называют также ее постоянной составляющей.

Замечание. Средним значением синусоиды, однако, обычно называют среднее значение ее модуля.

ВНИМАНИЕ ! Законы Кирхгофа выполняются для мгновенных и средних значений напряжений и токов, но не для действующих!

Действующие значения токов и напряжений показывают измерительные приборы электромагнитной системы. Стрелка таких приборов прикреплена к стальному сердечнику, который втягивается в неподвижную катушку с током. Как правило, эти приборы применяются для измерения синусоидальных напряжений и токов.

На шкале прибора электромагнитная система указывается значком

.

Средние значения токов и напряжений показывают приборы магнитоэлектрической системы. Стрелка таких приборов прикреплена к катушке с током, помещенной в магнитное поле постоянного магнита. Как правило, эти приборы применяются для измерения постоянных или медленно изменяющихся напряжений и токов.

На шкале прибора магнитоэлектрическая система указывается значком

.

Цифровые приборы обычно имеют два основных режима работы, один из которых предназначен для измерения постоянных величин, второй – для измерения действующих значений синусоидальных величин.

Для измерения средних значений переменных напряжений и токов, а также действующих значений несинусоидальных напряжений и токов нужно изучить паспорт прибора и узнать, допускает ли он такие измерения. Нужно учитывать также частотные ограничения измерительных приборов.

Тема 2. Синусоидальные режимы электрических цепей

11. Комплексный метод расчета синусоидальных режимов эл. Цепей.

Синусоидальным режимом эл. цепи называется такой режим, при котором все напряжения и токи цепи изменяются по синусоидальному закону с одной и той же частотой.

Синусоидальные напряжения и токи широко применяются в основном по следующим причинам:

1. Они легко получаются с помощью различных генераторов.

2. Они легко преобразуются трансформаторами.

3. С их помощью легко создаются вращающиеся и бегущие магнитные поля, используемые в электродвигателях.

4. Сложением синусоидальных колебаний можно получать различные несинусоидальные напряжения и токи.

Рис. 1.11.

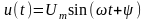Рассмотрим синусоидальное напряжение . Его характеризуют три параметра: амплитуда 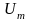, круговая частота 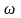и начальная фаза 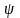(рис. 11.1). Амплитудные значения в электротехнике обозначаются большими буквами с индексом m.

К характеристикам синусоиды 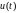относятся также действующее значение U, циклическая частота (т.е. количество колебаний в секунду), и период .

Синусоидальный ток 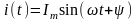характеризуется аналогичными параметрами .

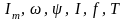Для любой синусоиды действующее значение и амплитуда связаны коэффициентом : .

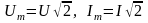Состояние эл. цепей в синусоидальных режимах можно описывать, пользуясь функциями времени. Однако, это громоздко и трудоемко. Поэтому для расчетов синусоидальных режимов применяется комплексный метод. Он позволяет заменить дифференциальные и интегральные уравнения элементов эл. цепи алгебраическими, а также весьма наглядно представить синусоиды в виде векторов на векторных диаграммах.

Основа метода состоит в том, что каждой синусоиде ставится в соответствие комплексное число, называемое комплексом. Такое соответствие взаимно однозначно. Оно определяется правилом:

,

где 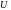– действующее значение синусоиды,  – начальная фаза синусоиды, 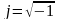 – мнимая единица (в электротехнике она обозначается этой буквой). Информация о частоте в комплекс не входит и должна учитываться отдельно. Комплексы обозначаются большими буквами с точкой: , или подчеркнутой большой буквой: .

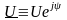Примеры: ,

.

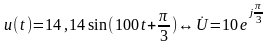Общая схема метода:

1. Переход от синусоид к комплексам.

2. Решение задачи в комплексах.

3. Переход от комплексов к синусоидам (если это нужно).

Рассмотрим произвольные синусоиды и 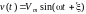, их комплексы и 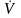, а также произвольное действительное число А. Операции на множестве синусоид и операции на множестве комплексов обладают следующим соответствием:

	Эти два свойства называются линейностью

Такое соответствие операций позволяет рассматривать множество синусоид и множество комплексных чисел как по существу один и тот же математический объект. Доказательство несложно и опирается на свойства синусоид и комплексных чисел.

Комплексы изображаются векторами на плоскости согласно обычным правилам, принятым для комплексных чисел. В электротехнике такие рисунки называются векторными диаграммами.

Стрелки на векторной диаграмме - это изображения синусоид, а стрелки на схемах эл. цепи - это направления вычисления напряжений и токов!

Благодаря линейности соответствия синусоид и комплексов законы Кирхгофа, а также все другие свойства и методы расчета линейных эл. цепей при переходе к комплексам сохраняются.

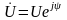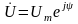Замечание 1: В качестве модулей комплексов мы приняли действующие значения синусоид: . Такие комплексы называются комплексами действующих значений. Однако, иногда бывает удобно принять в качестве модулей комплексов амплитудные значения синусоид: . Такие комплексы называются комплексными амплитудами.

Замечание 2: Любую синусоиду можно представить также в виде синус- и косинус-составляющих:

,

где , 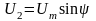. При этом , .

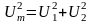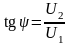Так как для комплексных амплитуд 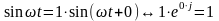, , то представление синусоиды в виде синус- и косинус-составляющих позволяет поставить ей в соответствие комплексную амплитуду в алгебраической форме:

.

Замечание 3: Комплексный метод применяется не только в электротехнике, но везде, где исследуются синусоидальные колебания.