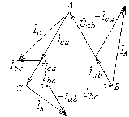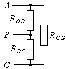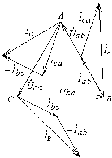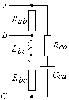- •Тема 1. Основные понятия и законы теории цепей. Электрические и магнитные цепи.
- •1. Основные термины теории электрических цепей
- •2. Первый закон Кирхгофа
- •3. Второй закон Кирхгофа.
- •4. Основные элементы линейных электрических цепей.
- •5. Эквивалентные преобразования фрагментов электрических цепей.
- •6. Мощность двухполюсника
- •7. Полная система расчетных уравнений эл. Цепи.
- •8. Метод узловых потенциалов
- •9. Магнитные цепи.
- •10. Основные характеристики переменных токов и напряжений.
- •Тема 2. Синусоидальные режимы электрических цепей
- •11. Комплексный метод расчета синусоидальных режимов эл. Цепей.
- •12. Резистор, катушка индуктивности и конденсатор в синусоидальном режиме.
- •13. Комплексное сопротивление и комплексная проводимость.
- •14. Мощность двухполюсника в синусоидальном режиме
- •15. Последовательное соединение резистора, катушки индуктивности и конденсатора.
- •16. Смешанное соединение резистора, катушки индуктивности и конденсатора.
- •17. Трехфазный источник напряжения. Общая характеристика трехфазных цепей.
- •18. Соединение трехфазного источника напряжения и нагрузки звездой
- •19. Соединение трехфазного источника напряжения и нагрузки треугольником
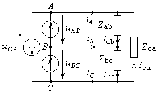
19. Соединение трехфазного источника напряжения и нагрузки треугольником
Рис. 19.1. |
Токи
 называются фазными, потому что это токи
фаз нагрузки. Токи
называются линейными, так как это токи
в линейных проводах.
называются фазными, потому что это токи
фаз нагрузки. Токи
называются линейными, так как это токи
в линейных проводах.
Напряжения являются одновременно фазными и линейными, так как это напряжения фаз источника и нагрузки, а также напряжения между линейными проводами.
Рассмотрим уравнения, описывающие состояние рассматриваемой цепи. Согласно уравнениям фаз нагрузки (по закону Ома):
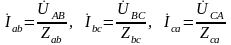 .
.
Рис. 19.2. |
|
Рис. 19.3. |
|
Рис. 19.4. |
|

Для пояснения уравнений построим векторные диаграммы. Рассмотрим некоторые конкретные типы нагрузок.
Простейший случай симметричной резистивной нагрузки показан на рис. 19.2. Из этой диаграммы видно, что для симметричной нагрузки
 .
.
На рис. 19.3 показана несимметричная резистивная нагрузка - в разных фазах разные резисторы.
На рис. 19.4 изображена диаграмма напряжений и токов несимметричной нагрузки, у которой в фазу ab включен резистор, в фазу bc – активно-индуктивный элемент, в фазу ca – активно-емкостной элемент. Главное отличие последнего случая от предыдущих – сдвиги фаз между напряжениями и токами в фазах bc и ca.
Рис. 19.5. |
 .
Это можно доказать, используя законы
Кирхгофа.
.
Это можно доказать, используя законы
Кирхгофа.
По определению
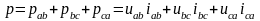 .
.
С другой стороны,

Здесь использованы выражения линейных
токов через фазные, а также равенства
 ,
,
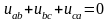 ,
последнее из которых представляет собой
2-й закон Кирхгофа для напряжений цепи.
,
последнее из которых представляет собой
2-й закон Кирхгофа для напряжений цепи.
В случае симметричной нагрузки можно измерить мощность только одной фазы и умножить ее на три.
Приложение.
Комплексные числа.
Введение.
Комплексные числа имеют три формы
записи. Алгебраическая форма
представляет число в виде
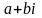 ;
здесь a и b – действительные
числа, i – число иного рода,
называемое мнимой единицей. Основное
свойство числа i состоит в том, что
его квадрат равен минус единице:
;
здесь a и b – действительные
числа, i – число иного рода,
называемое мнимой единицей. Основное
свойство числа i состоит в том, что
его квадрат равен минус единице:
 .
Числа вида
.
Числа вида
 являются действительными. Числа вида
являются действительными. Числа вида
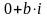 называются мнимыми.
называются мнимыми.
Обозначим число
буквой z . Число a называется
действительной частью числа z,
число b – мнимой частью числа z
. Коротко это можно записать так:
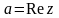 ,
,
 ,
где Re и Im – принятые в математике
обозначения действительной и мнимой
части комплексного числа (по-английски
Real – действительный, Imaginary – мнимый).
,
где Re и Im – принятые в математике
обозначения действительной и мнимой
части комплексного числа (по-английски
Real – действительный, Imaginary – мнимый).
Рис. 7.1.
 .
Поэтому его можно изобразить точкой на
плоскости. Действительная часть
откладывается по оси абсцисс, а мнимая
часть – по оси ординат (рис. 7.1).
.
Поэтому его можно изобразить точкой на
плоскости. Действительная часть
откладывается по оси абсцисс, а мнимая
часть – по оси ординат (рис. 7.1).
Комплексное число чаще изображают не точкой, а вектором, начало которого совпадает с началом координат комплексной плоскости, а конец имеет декартовы координаты . Если такой вектор перенести параллельно самому себе, он также будет изображать то же самое число.
Точку
на плоскости можно рассматривать и в
полярных координатах
 ,
где – расстояние
от точки до начала координат,
– угол между отрезком, соединяющим
точку с началом координат, и осью абсцисс
(рис. 7.1).
,
где – расстояние
от точки до начала координат,
– угол между отрезком, соединяющим
точку с началом координат, и осью абсцисс
(рис. 7.1).
Число
называется модулем
числа z , число
называется аргументом (или фазой)
числа z . Коротко это обозначается
так:
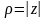 ,
,
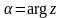 .
.
Из рис. 7.1 видно, что
 ,
,
 ,
(7.1)
,
(7.1)
поэтому комплексное число z можно представить в виде

Такая форма представления комплексного числа называется тригонометрической.
Отметим, что
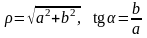 . (7.2)
. (7.2)
Формулы 7.1 определяют переход от тригонометрической формы комплексного числа к алгебраической, формулы 7.2 – от алгебраической к тригонометрической. При этом лежит в пределах от – до и вычисляется с учетом знаков a и b :

Для числа
 аргумент не определен.
аргумент не определен.
Формула Эйлера
 позволяет ввести показательную форму
комплексного числа:
позволяет ввести показательную форму
комплексного числа:
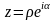 .
Модуль и фаза
имеют тот же смысл, что и для
тригонометрической формы комплексного
числа.
.
Модуль и фаза
имеют тот же смысл, что и для
тригонометрической формы комплексного
числа.
Формулу Эйлера можно понимать как
определение экспоненты с мнимым
показателем:
 – это такое комплексное число,
действительная часть которого равна
– это такое комплексное число,
действительная часть которого равна
 ,
а мнимая равна
,
а мнимая равна
 .
Более корректно функция
определяется как сумма ряда
.
Более корректно функция
определяется как сумма ряда
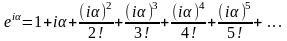 .
.
Учитывая, что и сгруппировав отдельно действительные и мнимые слагаемые этого ряда, получим ряды для косинуса и синуса, что и доказывает формулу Эйлера (строго говоря, такая перегруппировка слагаемых нуждается в обосновании, но мы законность этого действия примем без доказательства):

Для экспоненты с мнимым показателем, так же как и для экспоненты с действительным показателем, справедливо свойство: произведение двух экспонент равно экспоненте, показатель которой равен сумме показателей сомножителей:
 .
.
Сложение комплексных чисел
Рис. 7.2.
 и
и
 называется комплексное число
называется комплексное число
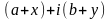 .
.
То есть, действительная часть суммы – это сумма действительных частей слагаемых, а мнимая часть суммы – это сумма мнимых частей слагаемых.
Например,
если
 ,
то
,
то
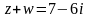 .
.
На комплексной плоскости сложению комплексных чисел соответствует сложение векторов (рис. 7.2).
Сложение чисел в показательной и тригонометрической форме неудобно. Чтобы сделать это, нужно сначала перевести оба числа в алгебраическую форму, сложить их, а затем перевести результат в нужную форму.
Например,
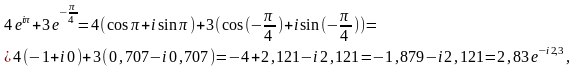
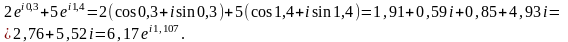
Умножение комплексных чисел
Умножение комплексных чисел в алгебраической форме выполняется по тем же правилам, что и умножение действительных чисел. Единственное различие в том, что :
 .
.
Например,
 .
.
Умножение комплексных чисел в показательной
форме выполняется еще проще. Пусть
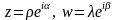 ,
тогда
,
тогда
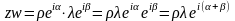 ,
,
то есть, при умножении комплексных чисел модуль произведения равен произведению модулей сомножителей, а аргумент произведения равен сумме аргументов сомножителей.
Например, 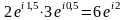 ;
;  .
.
С помощью формулы Эйлера из правила умножения комплексных чисел в показательной форме может быть получено правило умножения комплексных чисел в тригонометрической форме. Оно такое же, как для чисел в показательной форме.
Замечание 1: Мнимая единица может
записываться как перед действительным
множителем, так и после него:
 и т.д. Эти выражения равны вследствие
того что произведение любых двух
комплексных чисел коммутативно, т.е не
зависит от порядка сомножителей.
и т.д. Эти выражения равны вследствие
того что произведение любых двух
комплексных чисел коммутативно, т.е не
зависит от порядка сомножителей.
Замечание 2: Аргументы комплексных чисел могут выражаться как в радианах (то есть просто в числах), так и в градусах. Запись аргументов комплексных чисел в радианах, как правило, применяется в математике и физике; запись в градусах – в технических науках и инженерных расчетах.
Умножению комплексного числа z на
число
 соответсвует растяжение вектора,
изображающего число z, в
соответсвует растяжение вектора,
изображающего число z, в
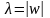 раз и поворот его на угол
раз и поворот его на угол
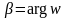 .
Это следует из описанных выше правил
умножения.
.
Это следует из описанных выше правил
умножения.
Деление комплексных чисел
Проще всего делить числа в показательной и тригонометрической форме. При этом модуль частного равен отношению модулей делимого и делителя, аргумент частного равен разности аргументов делимого и делителя. Это правило прямо следует из правил умножения.
Пусть
,
,
тогда
 .
.
Например,
 .
.
Чтобы разделить комплексное число в
алгебраической форме на действительное
число, нужно разделить отдельно
действительную и мнимую часть. Пусть
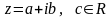 ,
тогда
,
тогда
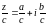 .
Например:
.
Например:
 .
.
Рис. 7.3.
Комплексно
сопряженное число обозначается
звездочкой или чертой наверху, например,
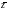 .
Комплексно сопряженные числа имеют
одну и ту же действительную часть и
противоположные мнимые части:
.
Комплексно сопряженные числа имеют
одну и ту же действительную часть и
противоположные мнимые части:
 .
На комплексной плоскости комплексно
сопряженные числа расположены симметрично
относительно действительной оси
(рис. 7.3). Произведение числа на его
сопряженное равно квадрату его модуля,
это всегда неотрицательное действительное
число:
.
На комплексной плоскости комплексно
сопряженные числа расположены симметрично
относительно действительной оси
(рис. 7.3). Произведение числа на его
сопряженное равно квадрату его модуля,
это всегда неотрицательное действительное
число:
 .
.
Итак,
разделим два числа в алгебраической
форме. Пусть
 ,
,
 .
.
Тогда
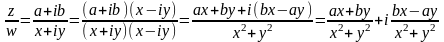 .
.
Например,
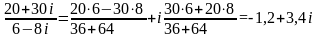 .
.