2.2.2. Радиационный теплообмен между неравномерно нагретыми участками поверхности

Предположим, имеются две площадки, имеющие разные температуры. Какое количество теплоты может быть передано от одной площадке к другой путем излучения. Вводиться понятие об угловых коэффициентах.

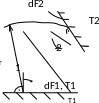
Рис. 2.14

φ_ik – угловой коэффициент, показывающий, какая доля излучения i-го участка попадает на поверхность k-ого участка.

Предполагается, что с участка поверхности dF₁ излучается тепловой поток Q₁₂, а с dF₂ – Q₂₁.

С каждой площадки dF₁ и dF₂ испускается полусферический поток.

Рис. 2.15

dF₂ : Q₁

dF₂: Q₂

φ_ik – отношение потоков, которое испускается с одной площадки в направлении r другому полному полусферическому потоку.

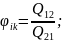
Свойства угловых коэффициентов

1. Свойство взаимозаменяемости.

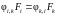, где i=1, n и k=1, n;

i=k – случай самооблучения поверхности

2. Свойство замыкаемости.

В замкнутых системах ; ;

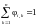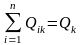3. Свойство затеняемости.

Смысл: поток излучения от участка 1 к участку 2 равен нулю, и соответственно 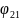=0, если на пути всех лучей находится непрозрачное тело ( =0).

Для участка с невогнутой поверхностью коэффициент 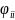=0.

Для вогнутых поверхностей пренебрегать самооблучением нельзя. Если защемить края, придем к модели абсолютно твердого тела .

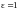4. Свойство распределительности.

Поток от участка 1 к участку 2 складывается между потоками отдельных частей участков.

Выражение для углового коэффициента в общем случае имеет следующий вид:

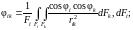
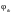находят методом контурного интегрирования.

Частные случаи:

1) речь идет о бесконечно протяженных пластинах

T₁>T₂

Рис. 2.16

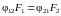(см. св-во 1);

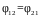в нашем случае (бесконечно протяженных пластин)

и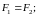

Поток между этими пластинами:

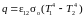(соответствует закону Стефана–Больцмана);

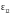– эффективная излучательная способность;

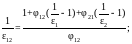
Таким образом, все, что первая пластинка излучает, попадает на вторую пластинку.

В общем случае

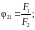
В нашем случае

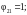
Так как излучающая пластина не вогнутая, ;

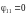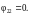
В итоге можем прийти к следующему выражению:

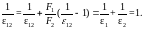
Угловые коэффициенты – параметры, зависящие исключительно от геометрических особенностей, вступающих в тепловое взаимодействие тел.

Для ряда простейших случаев имеются справочные таблицы.

2.2.3. Радиационный теплообмен в поглощающих и рассеивающих средах

Свойствами поглощения и рассеивания теплового излучения обладают потоки жидкости и газа, а также твердые тела. Наибольшее распространение в практике тепловых расчетов получила теория переноса излучения, основанная на представлениях (допущениях) геометрической оптики и соотношениях энергетического баланса.

Согласно феноменологическому подходу, рассеивающая среда рассматривается как набор эффективных рассеивающих неоднородностей или элементарных объемов, которые как-то разбросаны в пространстве. На каждой такой неоднородности излучение испытывает элементарный акт рассеивания с каким-то угловым распределением и далее происходит свободный пробег этого излучения до следующей неоднородности, на которой оно опять рассеивается. Вот, собственно говоря, основа феноменологических представлений. В основе аналитических представлений здесь лежит так называемое "уравнение переноса", которое формулирует энергетический баланс при таком рассеянии излучения и где главная величина – это лучевая интенсивность. Это поток энергии в заданные точки и в заданном направлении.

Уравнение переноса излучения в плоском слое поглощающей, излучающей и рассеивающей среды имеет следующий вид:

;

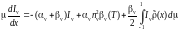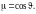
Рис. 2.17

Данное уравнение записано для случая азимутальной симметрии.

Составляющие уравнения:

Левая часть характеризует изменения интенсивности излучения внутри частично прозрачного материала

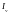– спектральная интенсивность излучения, количество энергии, которое распространяется в заданном спектральном диапазоне и проходит через единицу площади.

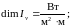
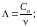
где μ – косинус направляющего угла ;

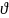Первый член правой части характеризует ослабления излучения внутри поглощающей и рассеивающей среды.

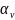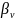– коэффициент поглощения; - коэффициент рассеивания;

_{dimα= м-1; dimβ= м-1;}

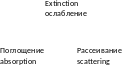
Коэффициент экстинкции æ=(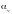 + 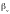) коэффициент ослабления.

Нагретая среда сама является источником теплого излучения. В частично прозрачных средах это излучение может распространяться внутри среды.

Второй член правой части следует из закона Клаузиуса

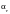
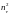
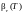
n – показатель преломления dim n= б/р.

У оконного стекла n ~ 1,55 на основе оксида кремния и других силикатных материалов.

Сам кремний: n ~ 4,0.

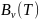– Функция Планка dim B= Вт/м²;

В простейшем случае (абсолютно черное тело):

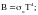
Таким образом, этот член характеризует количество энергии, испускаемой частично прозрачной нагретой средой. Показатель преломления газообразных сред: газы и вакуум n=1.

Эффекты рассеивания необходимо учитывать при расчете теплообмена внутри корпуса сопла РДТТ.

Последняя составляющая – столкновительный член, характеризует количество лучистой энергии, возвращаемой в заднюю точку за счет обратного рассеивания.

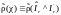– индикатриса рассеивания; I – интенсивность излучения; χ – угол между направлениями падающего и рассеянного луча;

_{μ’– косинус угла рассеивания;}

Уравнение переноса излучения является интегро-дифференциальным.

Прямое интегрирование его требует больших вычислительных ресурсов.

I=f(x, ,T,μ)

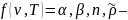представляют собой объемные оптические свойства.

Разработаны приближенные методы решения этого уравнения. Одним из них является метод моментов. Он предполагает введение интегральных параметров, связывающих интенсивность излучения и угловую переменную μ.

,

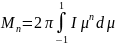где n=0,1,2, – порядок моментной аппроксимации;

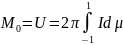– объемная плотность энергии излучения;

– плотность потока излучения.

Вводя моментную аппроксимацию можно заменить интегро-дифференциальное уравнение дифференциальным.

В этом случае можно записать:

;

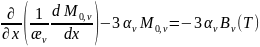В итоге требуется определить интегральную плотность потока излучения q_R.

;

Если речь идет не только об определении поля излучения (q_R(x)), а о том, сколько теплоты выделяется в каждом элементарном объеме, то необходимо вычислять другую характеристику.

Внутренние источники теплоты:

;

;

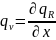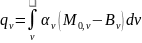1-ое приближение

Уравнение переноса излучения упрощается, если среда не излучающая (приближение холодного тела (ПХТ)).

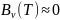; следовательно второй член меньше, чем два других члена, .

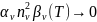Это приближение справедливо для некоторых видов лазерной техники, источников теплового излучения, так называемых солнечных бассейнов, предназначенных для получения пресной воды.

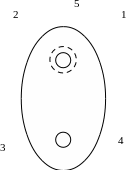
Рис. 2.18 Схема оптического квантового генератора

1– корпус отражателя; 2–лампа-вспышка (импульсный источник газоразрядного высоко интенсивного излучения); 3 – стержень из оптически активного материала (рубин); 4–охладитель (водо-спиртовая смесь); 5 – оптический фильтр (из стекла).

Второе приближение:

Нерассеивающая среда = .

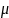
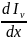Чисто поглащающая среда.