
- •1. Основные понятия и определения в области тепловых режимов летательных аппаратов
- •1.1. Терминология
- •1.2. Классификация теплонагруженных систем
- •2. Механизмы теплообмена
- •2.1. Теплопроводность
- •2.1.1. Уравнение теплопроводности и его формы
- •2.1.2. Условия однозначности для решения уравнения теплопроводности
- •2.1.3. Три стадии развития теплообмена
- •2.2. Излучение
- •2.2.1. Фундаментальные законы
- •2.2.2. Радиационный теплообмен между неравномерно нагретыми участками поверхности
- •2.2.3. Радиационный теплообмен в поглощающих и рассеивающих средах
- •2.3. Конвекция
- •3. Расчетная схема
- •4. Определение тепловых нагрузок
- •4.1. Теплообмен излучения космических аппаратов вблизи планет Солнечной системы
- •5. Аэродинамический нагрев
- •5.1. Понятие о пограничном слое
- •5.2. Особенности аэродинамического нагрева на больших высотах
- •6. Особенности тепловых режимов объектов ракетно-космической техники
- •6.1. Космические антенны
- •6.2. Надувные элементы конструкции. Плёночные конструкции
- •7. Приложение. Практические занятия
- •7.1. Температурное состояние тонкостенных элементов конструкции
- •7.1.1. Задача №1
- •1.Геометрическая модель
- •2.Физическая модель– система допущений
- •Математическая модель
- •Метод решения.
- •7.1.2. Задача №2
- •Геометрическая модель
- •Физическая модель
- •Математическая модель
- •7.1.3. Задача № 3: Температурное состояние тонкостенного насадка сопла.
- •Геометрическая модель.
- •Физическая модель
- •Математическое моделирование
- •Метод решения.
Метод решения.
Выполнение преобразований.
Вводятся
параметры:
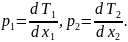
И вместо уравнений (1) получаем систему:
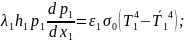 (1а)
(1а)
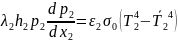 ,
(1б)
,
(1б)
где
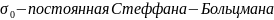 .
.
Решение этих уравнение учетом граничных условий дает:
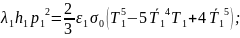 (5)
(5)
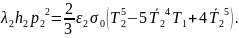 (6)
(6)
С
помощью уравнения (4) определяется
значение
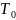
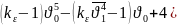 (7)
(7)
Введены следующие обозначения
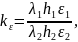
где
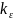 –
безразмерный параметр радиационного
кондуктивного теплообмена. В
соседствуют параметры, отвечающие за
отвод теплоты в пространство,
–
безразмерный параметр радиационного
кондуктивного теплообмена. В
соседствуют параметры, отвечающие за
отвод теплоты в пространство,
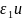
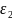 и коэффициенты теплопроводности/коэффициенты
кондуктивного теплообмена
и коэффициенты теплопроводности/коэффициенты
кондуктивного теплообмена
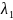 и
и
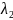 .
.
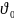 – представляет
собой безразмерную температуру.
– представляет
собой безразмерную температуру.
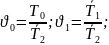
Наиболее
простой случай соответствует
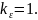 В этом случае:
В этом случае:
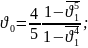
При
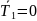 (случай
гипотетический, обл. 1 –в абсолютной
тени).
(случай
гипотетический, обл. 1 –в абсолютной
тени).
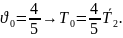
После определения каждое из уравнений (1) и (2) можно решить независимо.
7.1.2. Задача №2
Температурное состояние оболочки бака, частично заполненного жидкостью.
Геометрическая модель
Распределение температуры в жидкости и над зеркалом жидкости.
На внешней поверхности бака, а также над зеркалом жидкости коэффициент теплоотдачи отличается от и в жидкости.
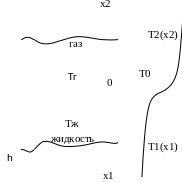
Рис. 7.3
Содержательная постановка задачи: бак частично заполнен криогенной жидкостью. Имеется значительный перепад температур вдоль поверхности бака. Интерес представляет оценка этого перепада и, главным образом, характер изменения в зоне раздела между жидкостью и баком.
Важно установить степень влияния на распределение температуры, характеристик теплообмена (коэффициента теплоотдачи и температуры) и теплофизических свойств.
Физическая модель
Процессы теплообмена одномерные, стационарные. Температура в стенке бака изменяется только вдоль поверхности и постоянна в каждом сечении по толщине.
Коэффициент теплоотдачи в жидкости >> чем в газе:
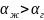 ;
;Коэффициенты теплоотдачи
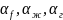 – постоянны;
– постоянны;Форма и размеры бака не изменяются h=const.
Математическая модель
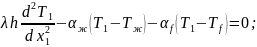 (1)
(1)
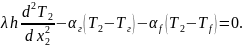 (2)
(2)
(1), (2) – обыкновенные дифференциальные уравнения 2-го порядка.
Для получения однозначного решения к каждому из этих уравнений необходимо присоединить по 2 граничных условия:
При
 и при
и при
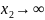 имеем
имеем
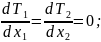 (3)
(3)
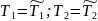 .
.
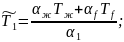
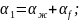
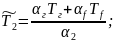
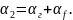
И второе граничное условие, которое выражает неразрывность температур и тепловых потоков:
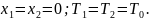
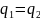 или
или
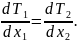 (4)
(4)
4.Метод решения
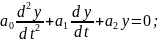 (а)
(а)
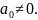
Решением является:
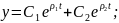 (б)
(б)
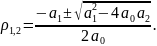
При
условии, что
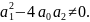
Другой вариант решения:
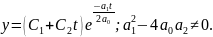 (в)
(в)
В
этом случае (в), если
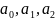 действительны, то при
действительны, то при
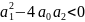 ,
корни
,
корни
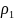 и
и
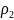 будут комплексными, и вместо (б) имеем
следующее решение:
будут комплексными, и вместо (б) имеем
следующее решение:
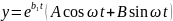 ;
;
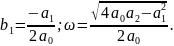 (г)
(г)
Решение уравнений (1), (2) с учетом граничного условия (3) имеет вид:
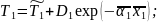
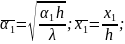 (5)
(5)
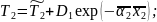
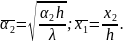
С учетом граничных условий (4) из (5) можно получить:
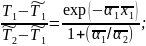
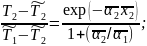
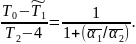
При получении численных результатов следует принять во внимание, что exp(-3)~0,05=е-3 – примерная точность нижеприведенных расчетов. А следовательно, на практике можно считать, что неравномерность распределения температуры будет сказываться лишь в зоне:
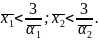
Первое значение характерно для практически безветренной погоды, второе – при довольно интенсивном обдуве корпуса ракеты потоком ветра.
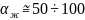 Вт/(м2К);
Вт/(м2К);
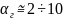 Вт/(м2К);
Вт/(м2К);
Толщина
стенки бака:
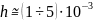 м;
м;
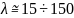 Вт/(мК)
– первое значение для нержавеющих
сталей, а второе для хорошо проводящих
тепло материалов (типа алюминиево-магниевых
или литиево-алюминиевых).
Вт/(мК)
– первое значение для нержавеющих
сталей, а второе для хорошо проводящих
тепло материалов (типа алюминиево-магниевых
или литиево-алюминиевых).
В
итоге если положить
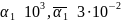
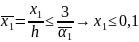 м
м
Если
представить, что
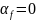 (в космическом пространстве), можно
написать, что:
(в космическом пространстве), можно
написать, что:
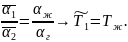
Отношение αж/αг обычно велико, и поэтому температура мало отличается от температуры жидкости. В этом случае температуру всей смоченной части бака можно считать равной температуре жидкости.
