
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
- •Комплексна контрольна робота з математики
Розглянуто та схвалено на ЗАТВЕРДЖУЮ
засіданні методичної комісії Директор ЯПЛЗТ
Протокол №____від_______ ________В.Я.Петренко
Голова метод. комісії ______Руснак О.П.
КОМПЛЕКСНІ КОНТРОЛЬНІ ЗАВДАННЯ
З МАТЕМАТИКИ
Номери завдань до комплексної контрольної роботи з математики («Збірник завдань для державної підсумкової атестації з математики. 11 клас.» авт. Істер О.С. та інші. – К.: Центр навчально-методичної літератури, 2012)
ВАР |
1 (початковий рівень – 1б) |
2 (середній рівень – 2б) |
3 (достатній рівень – 4б) |
4 (високий рівень – 5б) |
1 |
1.5 |
1.12 |
2.1 |
3.3 |
2 |
1.7 |
1.12 |
2.2 |
3.3 |
3 |
1.7 |
1.12 |
2.2 |
3.3 |
4 |
1.7 |
1.12 |
2.1 |
3.3 |
5 |
1.5 |
1.12 |
2.1 |
3.3 |
6 |
1.5 |
1.12 |
2.2 |
3.3 |
7 |
1.5 |
1.12 |
2.1 |
3.3 |
8 |
1.5 |
1.12 |
2.1 |
3.3 |
9 |
1.5 |
1.12 |
2.1 |
3.3 |
10 |
1.5 |
1.12 |
2.1 |
3.3 |
11 |
1.7 |
1.12 |
2.2 |
3.3 |
12 |
1.5 |
1.12 |
2.1 |
3.3 |
13 |
1.5 |
1.12 |
2.2 |
3.3 |
14 |
1.5 |
1.12 |
2.1 |
3.3 |
15 |
1.5 |
1.12 |
2.1 |
3.3 |
16 |
1.5 |
1.12 |
2.2 |
3.3 |
17 |
1.5 |
1.12 |
2.1 |
3.3 |
18 |
1.5 |
1.12 |
2.2 |
3.3 |
19 |
1.7 |
1.12 |
2.2 |
3.3 |
20 |
1.5 |
1.12 |
2.2 |
3.3 |
21 |
1.5 |
1.12 |
2.2 |
3.3 |
22 |
1.7 |
1.12 |
2.1 |
3.3 |
23 |
1.5 |
1.12 |
2.1 |
3.3 |
24 |
1.5 |
1.12 |
2.1 |
3.3 |
25 |
1.5 |
1.12 |
2.2 |
3.3 |
26 |
1.5 |
1.12 |
2.1 |
3.3 |
27 |
1.5 |
1.12 |
2.1 |
3.3 |
28 |
1.5 |
1.12 |
2.2 |
3.3 |
29 |
1.7 |
1.12 |
2.1 |
3.3 |
30 |
1.5 |
1.12 |
2.3 |
3.3 |
Комплексна контрольна робота з математики
ВАРІАНТ №1
Графік якої з запропонованих функцій зображено на рисунку?
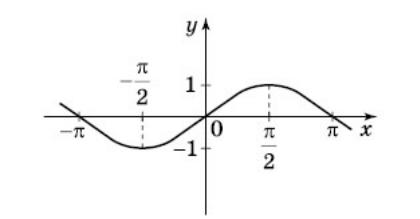
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1 бал
Пряма
 паралельна площині
паралельна площині
 ,
а пряма
,
а пряма
 належить площині
.
Як можуть бути розташовані прямі
і
?
Виберіть правильне твердження.
належить площині
.
Як можуть бути розташовані прямі
і
?
Виберіть правильне твердження.
А) прямі і можуть бути паралельними, не можуть бути мимобіжними або перетинатися;
Б) прямі і можуть бути мимобіжними, не можуть бути паралельними або перетинатися;
В) прямі і можуть перетинатись, не можуть бути паралельними або мимобіжними;
Г) прямі і можуть бути паралельними або мимобіжними, не можуть перетинатись.
2 бали
Розв’яжіть рівняння
 .
.
4 бали
Висота конуса дорівнює діаметру його основи. Знайдіть відношення площі його основи до площі бічної поверхні.
5 балів
Комплексна контрольна робота з математики
ВАРІАНТ №2
Скільки трицифрових чисел можна записати за допомогою цифр 4, 5 і 6, якщо цифри у числі не повторюються?
А) 4; Б) 6; В) 8; Г) 12.
1 бал
Площини квадратів
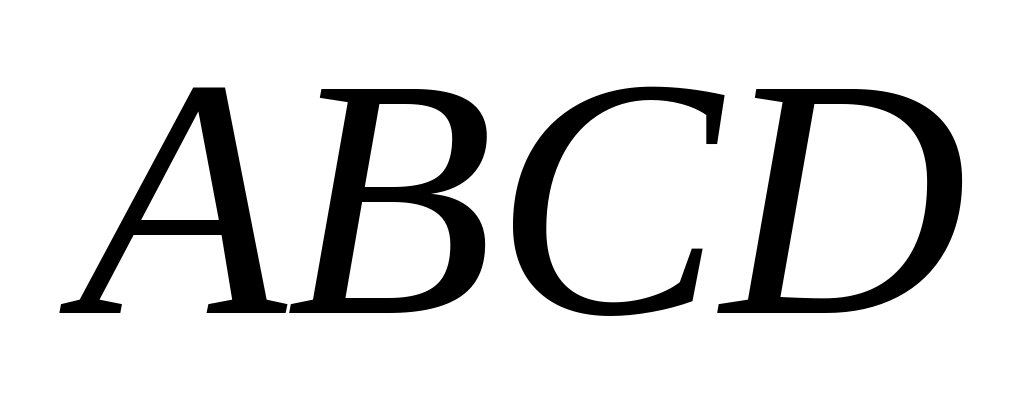 і
і
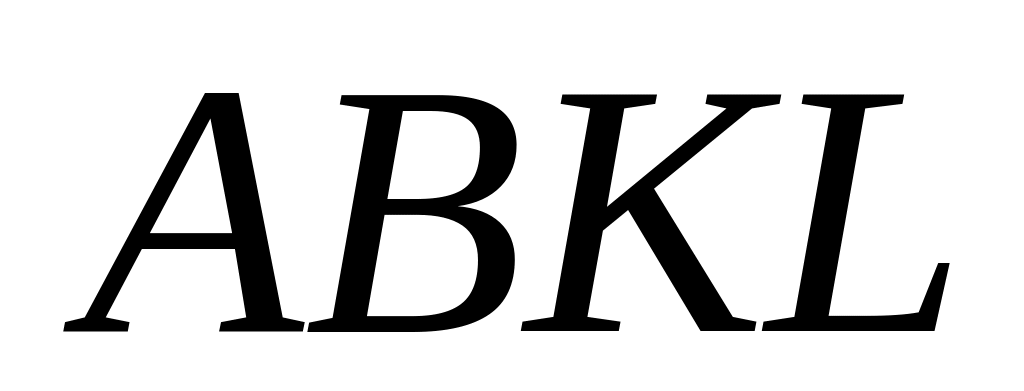 перпендикулярні,
перпендикулярні,
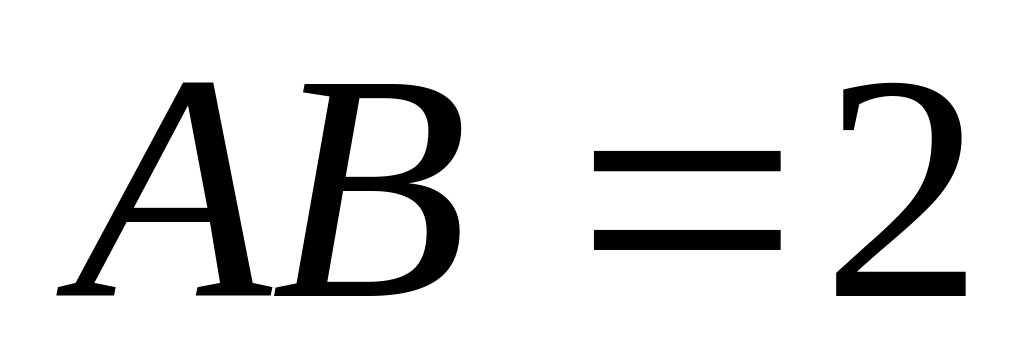 см.
Знайдіть відстань між точками
см.
Знайдіть відстань між точками
 і
і
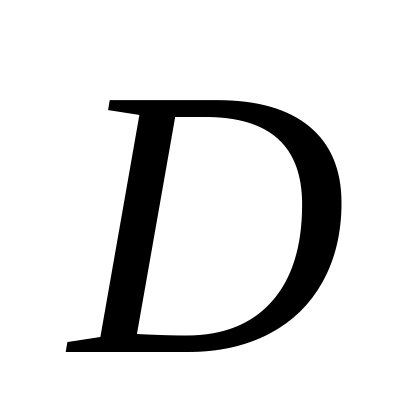 .
.
А) ![]() см; Б)
см; Б) ![]() см; В)
см; В) ![]() см; Г)
см; Г) ![]() см.
см.
2 бали
Розв’яжіть рівняння

4 бали
4. Основою прямого паралелепіпеда є паралелограм зі сторонами 3 м і 4 м. Одна з діагоналей паралелепіпеда дорівнює 5 м, а інша – 7 м. Знайдіть об’єм паралелепіпеда.
5 балів
Комплексна контрольна робота з математики
ВАРІАНТ №3
Знайдіть загальний вигляд первісних для функції
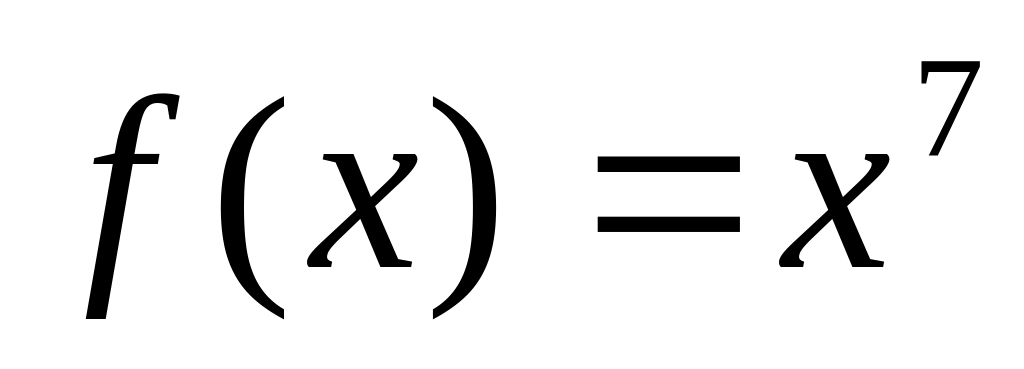
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1 бал
Знайдіть довжину вектора
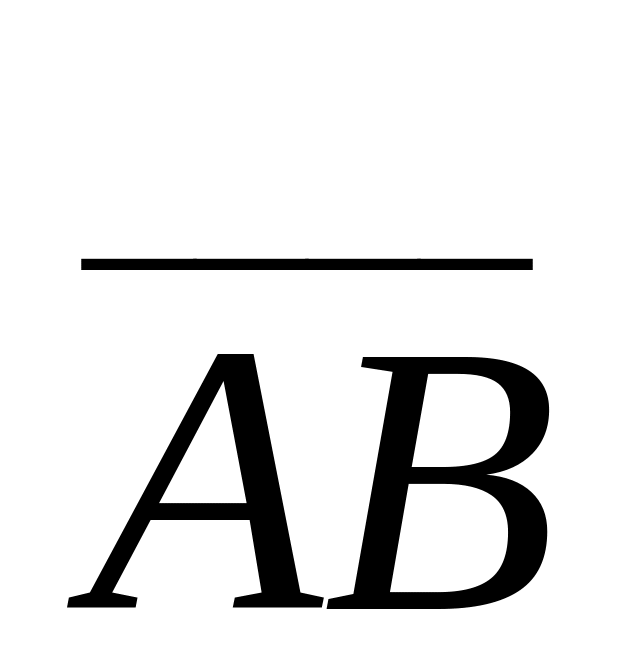 ,
якщо
,
якщо
 ,
,
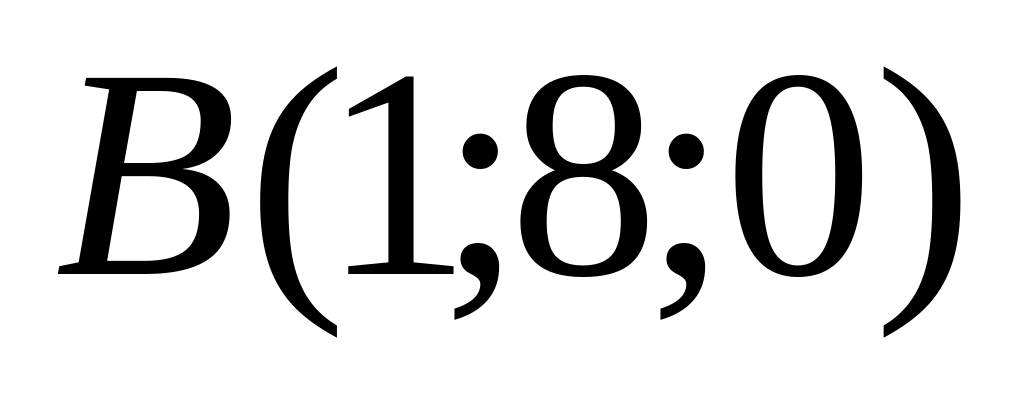 .
.
А) 3; Б) 5; В) 7; Г) 8.
2 бали
Є 6 різних блокнотів і 7 ручок. Скількома способами можна вибрати набір з 3 блокнотів і 2 ручок.
4 бали
Бічні ребра трикутної піраміди взаємно перпендикулярні. Кожне бічне ребро дорівнює а. Знайдіть об’єм піраміди.
5 балів
Комплексна контрольна робота з математики
ВАРІАНТ №4
Чому дорівнює
 ?
?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1 бал
У правильній трикутній призмі сторона основи дорівнює 3 см, а діагональ бічної грані – 5 см. Знайдіть площу бічної поверхні призми.
А) 27см2; Б) 36см2; В) 48см2; Г) 45см2.
2 бали
Знайдіть
 ,
якщо
,
якщо
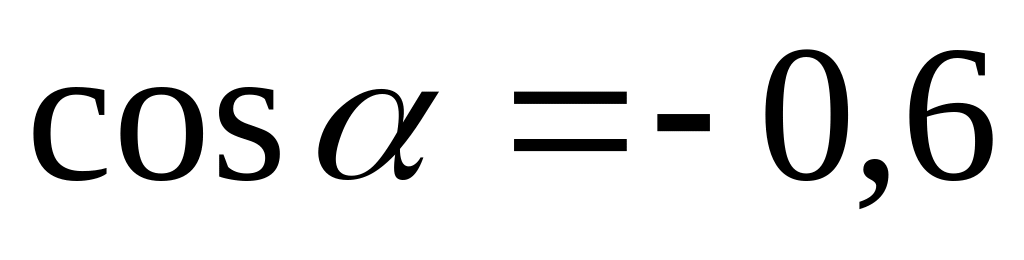 ;
;
 .
.
4 бали
У правильній чотирикутній зрізаній піраміді площі нижньої та верхньої основ відповідно дорівнюють Q і q, а бічне ребро утворює з площиною основи кут 45о. Знайдіть площу діагонального перерізу цієї зрізаної піраміди.
5 балів
Комплексна контрольна робота з математики
ВАРІАНТ №5
Чому дорівнює
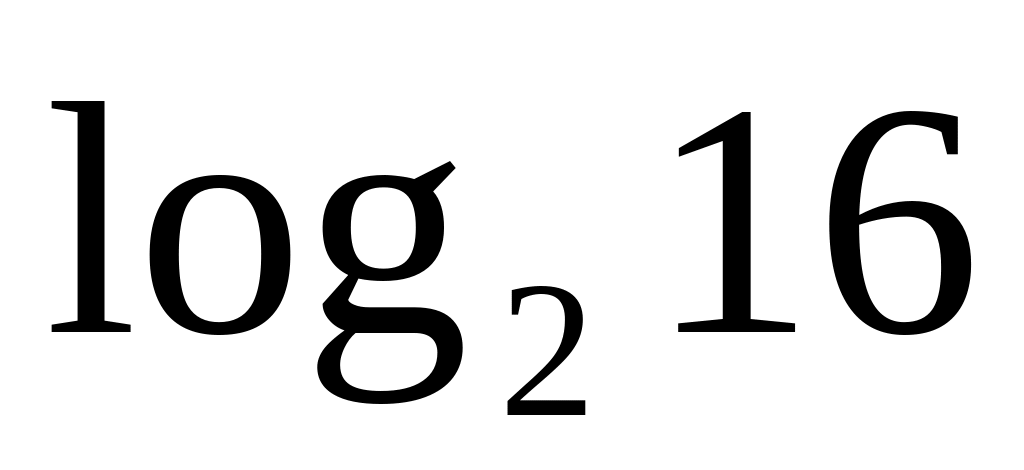 ?
?
А) 2; Б) 4; В) 8; Г) 16.
1 бал
Сторона основи правильної чотирикутної піраміди дорівнює 3см, а апофема – 4см. Знайдіть площу поверхні піраміди.
А) 33см2; Б) 30см2; В) 24см2; Г) 42см2.
2 бали
Розв’яжіть рівняння
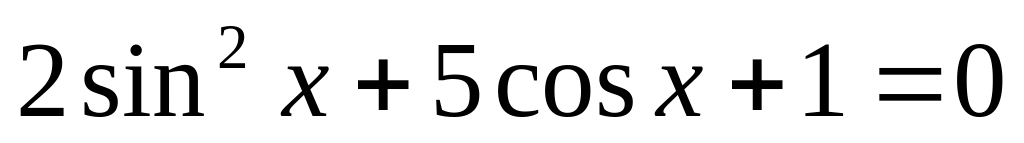
4 бали
Кулю перерізано двома паралельними площинами так. Що площі утворених перерізів дорівнюють 25π см2 і 144π см2. Центр кулі лежить між площинами, а відстань між ними дорівнює 17 см. Знайдіть площу поверхні кулі.
5 балів
