5. Основы цифровой электроники
Цифровая электроника благодаря своим преимуществам в настоящее время прочно завоевала место в различных отраслях техники.
Цифровые ЭВМ нашли широкое распространение, победив ЭВМ других типов. Уже в середине прошлого века благодаря своей точности и широкому кругу решаемых задач. В настоящее время цифровая электроника внедряется в устройствах связи, в бытовых приборах (мобильные телефоны, цифровые телевизоры и радио). Параметры известных ранее приборов с внедрением цифровой электроники существенно улучшаются. «Атомом» устройства цифровой электроники является транзистор (большей частью полевой), работающий в режиме ключа – или он представляет собой разрыв электрической цепи, или закоротку. Таким образом он имеет два состояния, которые можно оценить цифрами в двоичной системе: ноль или единица. Отсюда и название электроники, выполненной на таких «атомах» - цифровая. Цифры реализуются в устройствах цифровой электроники с помощью импульсов. Приближенно можно считать наличие импульса за единицу, а его отсутствие - за ноль.
Все задачи в устройствах цифровой электроники решаются с помощью с помощью логических элементов, взаимодействующих по законам алгебры логики (алгебра Буля). Буль - английский ученый, разработавший алгебру логики в позапрошлом веке, задолго до появления цифровой электроники.
Основные логические элементы цифровой электроники, их обозначения, уравнения Булевой алгебры приводятся ниже.
Повторитель
Y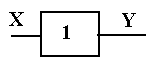
= X, т.е. если X
= 1, то Y = 1; если X
= 0, то Y = 0
Инвертор (схема «НЕ»)
,
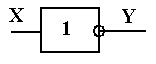т.е. если X = 1, то Y
= 0; если X = 0, то Y
= 1
3. Схема логического сложения (схема «ИЛИ»)
Y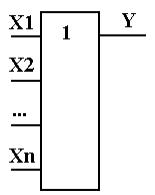
= X1 + X2 + … +
Xn
Т.е. Y = 1, если ИЛИ X1, ИЛИ X2, …, ИЛИ Xn равны 1;
Y = 0, если X1, X2, …, Xn все равны 0.
4. Схема логического умножения (схема «И»)
Y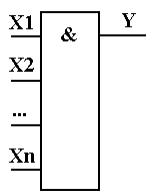
= X1 * X2 * … *
Xn
Т.е. Y = 1, если И X1, И X2, …, ИИ Xn равны 1;
Y = 0, если хотя бы один из X1, X2, …, Xn равен 0.