
- •Элементы выпуклого анализа.
- •Основная задача выпуклого программирования. Седловая точка и оптимальный план.
- •Теорема Куна-Таккера.
- •Критерий оптимальности для гладкой выпуклой задачи .
- •Теория двойственности в выпуклом программировании.
- •Решение одной задачи выпуклого программирования.
- •О существовании решения линейной задачи.
- •Задача на безусловный минимум.
- •Задача с равенствами. Метод исключения.
- •3.2.1 Метод исключения
- •10. Задача с равенствами. Обобщенное правило Лагранжа.
- •Задача с равенствами. Классическое правило множителей Лагранжа
- •Задача с равенствами. Лемма о включении
- •Задача с равенствами. Необходимое условие оптимальности первого порядка
- •Задача с равенствами. Другое доказательство принципа Лагранжа
- •Задача с равенствами. Случай линейных ограничений
- •Задача с равенствами. Условия оптимальности второго порядка
- •Задача с неравенствами. Необходимое условие оптимальности первого порядка
- •Задача снеравенствами. Обобщённое правило множителей Лагранжа
- •Задача с неравенствами. Классическое правило множителей Лагранжа
- •Задача с неравенствами. Условие оптимальности второго порядка
- •Векторная оптимизация. Эффективные планы. Усреднение целевых функций.
- •Принципы выбора
- •1. Введение весовых коэффициентов
- •2. Введение иерархии целевых функций
- •3. Установление гарантированных уровней
- •4. Минимизация расстояния до идеальной точки
Задача с равенствами. Классическое правило множителей Лагранжа
Пусть дана задача:
![]() (1)
(1)
Первоначально
Лагранж считал, что в теореме 1 можно
для любых задач положить
![]() ,
то есть правило справедливо для
классической функции Лагранжа. Однако
это было ошибкой. Покажем это на следующем
примере.
,
то есть правило справедливо для
классической функции Лагранжа. Однако
это было ошибкой. Покажем это на следующем
примере.
Оказывается, что из задачи (1) можно выделить такой подкласс, который с одной стороны является очень широким (практически все важные и интересные задачи принадлежат ему), а с другой стороны, для которого правило Лагранжа справедливо в классической форме.
Определение. Некоторый план задачи (1) (здесь необязательно оптимальный) будем называть обыкновенным, если вектора
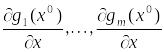 (7)
(7)
линейно независимы .
Теорема 2
(Классическое правило множителей
Лагранжа). Если
– обыкновенный локально-оптимальный
план задачи (1), то всегда найдётся такой
единственный классический вектор
Лагранжа
![]() ,
что выполняется условие:
,
что выполняется условие:
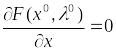 (8)
(8)
Доказательство. Пусть
– обыкновенный локально-оптимальный
план. В силу локальной оптимальности
для него справедлива теорема 1. В
частности, условия (5) или (5*). Докажем,
что в силу обыкновенности в (5*) множитель
![]() .
Предположим противное, то есть
.
Предположим противное, то есть
![]() .
Тогда из условия (5*) получаем
.
Тогда из условия (5*) получаем
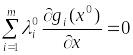 ,
(9)
,
(9)
в котором не все
множители
![]() нулевые. Тогда (9) означает линейную
зависимость векторов
и
противоречит обыкновенности
.
нулевые. Тогда (9) означает линейную
зависимость векторов
и
противоречит обыкновенности
.
Итак,
.
Разделим тогда выражение (5*) на
![]() и переобозначим:
и переобозначим:
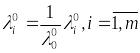 ,
тогда придём к условию (8).
,
тогда придём к условию (8).
Докажем единственность
.
Предположим противное. Найдётся ещё
один вектор Лагранжа
![]() такой, что
такой, что
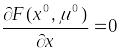 .
Вычитая из этого равенства равенство
(8), придём к
.
Вычитая из этого равенства равенство
(8), придём к
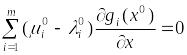 ,
причём не все коэффициенты
,
причём не все коэффициенты
![]() .
Это означает линейную зависимость
векторов (7) и снова противоречит
обыкновенности
.
.
Это означает линейную зависимость
векторов (7) и снова противоречит
обыкновенности
.
Ч.т.д.
Обсуждение. Теорема 1 и теорема 2 вместе составляют так называемый принцип Лагранжа снятия ограничений в задаче (1). Согласно которому и оптимальный план, и все локально оптимальные планы должны удовлетворять либо (5), либо (8), и поэтому должны находится среди решений систем
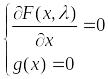 (10)
(10)
для обыкновенного плана и
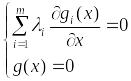 (11)
(11)
если не является обыкновенным.
Каждая из систем
(10) и (11) представляет собой систему
уравнений относительно
неизвестных
![]() .
Среди решений этих систем и только среди
них нужно искать
.
.
Среди решений этих систем и только среди
них нужно искать
.
Определение. Задача (1) называться нормальной, если – обыкновенный оптимальный план.
Определение.
Пара
![]() называется условно-стационарной
точкой
задачи (1),если она является решением
системы (10).
называется условно-стационарной
точкой
задачи (1),если она является решением
системы (10).
Принцип Лагранжа или теорему 2 можно переформулировать:
Если
– локально-оптимальный план, то его
нужно искать среди условно-стационарных
точек задачи (1). Так как
![]() ,
то система (10) может быть записана в
виде:
,
то система (10) может быть записана в
виде:
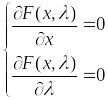 (10*)
(10*)
Таким образом, условно-стационарные точки как бы являются решением задачи на безусловный экстремум:
![]() .
.
