Критерий оптимальности для гладкой выпуклой задачи .
Рассмотрим задачу
(15)
– выпуклая функция,
– выпуклое множество,
.
Функцию
переменных, около некоторой точки
(в малой окрестности) можно разложить
в ряд Тейлора
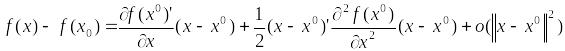(16)
Разложение (16)
справедливо лишь для
в малой окрестности точки
.
Теорема 3. Для
того чтобы
был оптимальным планом задачи (15)
необходимо и достаточно, чтобы
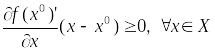(17).
А в случае, когда
,
то (17) эквивалентно условию стационарности
.
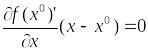(18)
Доказательство.
Необходимость.
Пусть
– оптимальный план задачи (15). Возьмем
произвольную точку
и построим точку
.
Если
достаточно мало, то точка
лежит в сколь угодно малой окрестности
.
Запишем разложение:
.
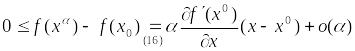Так как левая
часть равенства
,
то неотрицательно и первое слагаемое
справа. А так как
,
то приходим к (17).
Пусть теперь к
тому же
– внутренняя точка. Построим вектора
.
При достаточно малом
.
Подставляя его в (17):
.
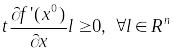Так как
,
то
.
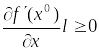Из этого неравенства следует (18).
Если предположить
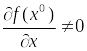и положить
,
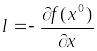то придем к противоречию.
Достаточность.
Пусть выполняется (17). Докажем, что
– оптимальный план задачи (15). Так как
функция
– гладкая и выпуклая, то для нее
выполняется гладкий критерий выпуклости:
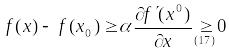
оптимальный
план.
Ч.т.д.
Из этой теоремы и
теоремы Куна-Таккера следует схема
исследования гладкой основной задачи
выпуклого программирования (
,
).
Пусть
оптимальный план такой задачи. Тогда
по теореме Куна-Таккера для нее выполняется
неравенство:
.
Если рассмотрим правую часть неравенства,
то оно означает, что на множестве
(выпуклом) функция
достигает своего минимума в точке
,
то есть оптимальный план основной задачи
выпуклого программирования является
оптимальным планом задачи
(19). А
функция
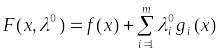является выпуклой и гладкой, то есть
задача (19) такая же как и (15). В частности,
если предположить, что
,
то для
должно выполняться неравенство
.
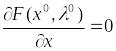(20)
Поэтому задачу нахождения оптимального плана основной задачи выпуклого программирования или задачу нахождения седловой точки можно свести к алгебраической задаче решения системы уравнений.
1) Сначала оптимальный план ищется на внутренности множества , то есть предполагаем, что . В силу вышесказанного и теоремы Куна-Таккера следует, что седловую точку надо искать среди решения системы уравнений
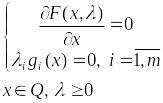(21)
Первое уравнение
следует из (20), а второе – из условия
дополняющей не жесткости. Решение
системы (21) относительно неизвестных
будем называть условно-стационарными
точками.
Ясно, что если – седловая точка функции Лагранжа, , то эта пара – условно-стационарная точка.
Система уравнений
(21) относительно переменных
представляет собой систему из
уравнений и
переменных.
Пусть мы нашли все
условно-стационарные точки. Тогда если
– одна из них, то подставляем ее в двойное
неравенство и проверяем его справедливость.
Если оно верно, то мы построили седловую
точку и можно записать ответ:
.
Если же это неравенство неверно
(нарушается хотя бы для одного
или хотя бы одного
),
то
не является оптимальным планом. Проверив
все условно-стационарные точки поочередно,
мы либо найдем оптимальный план задачи,
либо докажем, что его нет на
.
2) Оптимальный план
может находиться и на границе
.
Так как множество
имеет простую структуру, то его граница
простая, то есть состоит из некоторых
частей плоскостей, ребер, угловых точек.
Разбиваем
на отдельные элементы:
,
причем на каждом таком элементе либо
одна, либо несколько переменных задачи
фиксированы.
.
Перебирая поочередно все элементы границы, на каждом из них рассмотрим основную задачу выпуклого программирования, а так как там некоторые переменные фиксированы, то задача упрощается – имеет меньшее количество неизвестных, но она все равно относится к типу основных задач выпуклого программирования. Снова упрощенную задачу исследуем, как и на первом этапе, то есть строим систему, подобную (21), но более простую, находим условно-стационарные точки и каждую из них проверяем на седловую для исходной задачи.
Замечание. Условно-стационарную точку, найденную на границе, подставляем в двойное неравенство для функции Лагранжа исходной задачи, а не упрощенной.
Если мы построим седловую точку (докажем двойное неравенство), то процесс исследования прекращается и записывается ответ. Если же перебрав все элементы границы и все условно-стационарные точки, мы нигде не обнаружим седловой точки, то это означает, что у исходной основной задачи выпуклого программирования нет оптимального плана и на , а значит и вообще.