1. Введение весовых коэффициентов
Пусть в дополнении
к задаче (1) указаны числа
,
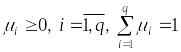которые можно интерпретировать как
степень (меру) важности
ой
целевой функции в задаче (1). Тогда за
векторно-оптимальный план принимается
решение задачи скалярной минимизации.
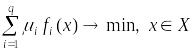(4)
Обычно при применении
этого принципа выбора исследователю
требуется самому указать значения
.
Это делается следующим образом:
выбирается некоторый план , который по оценке экспертов можно рекомендовать в качестве решения задачи (1). Тогда полагая
.
Затем приступаем к решению задачи (4).
Часто при применении этого принципа выбора все целевые функции предварительно оцениваются по одной шкале, потом выбирается, и подсчитываются коэффициенты. Если экспертной оценки нет, то в качестве можно выбирать один из эффективных планов.
2. Введение иерархии целевых функций
Пусть целевые
функции задачи (1) упорядочены по убыванию
важности:
.
Эта операция означает, что самая важная
целевая функция,
следующая по важности
и так далее, а самая маловажная функция
.
Пусть задаются числа
,
которые означают уступку по
ой
целевой функции от некоторого достигнутого
значения. Тогда векторно-оптимальный
план находится с помощью следующего
процесса:
I этап. Решается задача:
Находится её
решение – скалярно-оптимальный план
.
Затем делается уступка: строится
множество
.
II этап. Решается задача:
Пусть
– оптимальный план этой задачи, делается
уступка: строится множество
.
этап.
Решается задача:
и её решение объявляется векторно-оптимальным планом.
Обычно этот принцип
выбора осуществляется в виде диалога
между лицом, принимающим решение
(директором, начальником и т.д.) и
исследователем. Сначала исследователь
выясняет у лица, принимающего решение
иерархию целевых функций, затем
осуществляется первый этап. После того,
как построено
исследователь покажет значение самой
важной целевой функции и остальных на
этом плане и выяснит, согласно ли лицо,
принимающее решение сделать уступку и
в каком размере от самой важной целевой
функции в пользу остальных, если не
согласен, то
принимается за векторно-оптимальный
план. Если согласен, то указывает
и осуществляется второй этап, и на нем
снова повторяется диалог и так далее.
3. Установление гарантированных уровней
Пусть среди целевых
функций выделена самая главная
,
а по остальным целевым функциям указаны
верхние пределы числа
,
которые они не должны превышать. Тогда
в качестве векторно-оптимального плана
принимается задача скалярного минимума:
,
.
При реализации
этого принципа выбора обычно числа
нужно построить. Наиболее часто при
этом решается задача (2) и полагается
,
где
– уступки, которые выясняются в процессе
диалога с лицом, принимающим решение.
Например, если уступка не должна превышать
10%, то полагается,
.
4. Минимизация расстояния до идеальной точки
В этом случае сначала вычисляется идеальная точка с помощью решения задачи (2). Она имеет вид:
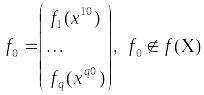
В качестве
векторно-оптимального плана принимается
решение:
.
Другими словами, идеальная точка
проектируется на множество
,
то есть находится точка, которая находится
на наиболее близком расстоянии и
векторно-оптимальный план – прообраз
проекции.