1. Элементы выпуклого анализа.

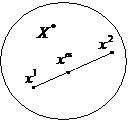
Определение. Подмножество называется выпуклым, если оно наряду с любыми своими точками целиком содержит и отрезок, их соединяющий .

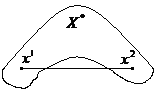
Определение. Множество называется строго выпуклым, если его граница не содержит прямолинейных отрезков, или .

Примеры выпуклых множеств: все пространство, гиперплоскость, -мерный куб, шар, прямая.

Невыпуклые множества: кривая поверхность, кривая линия, тор.

Свойства:

1) Пересечение любого числа выпуклых множеств, даже бесконечного, является снова выпуклым множеством.

Для объединения это несправедливо.

2) Для любого невыпуклого подмножества можно ввести понятие его выпуклой оболочки как пересечение всевозможных выпуклых множеств, его содержащих.

Определение. Говорят, что два подмножества в отделимы, если существует такая гиперплоскость, которая разбивает пространство на два полупространства и эти множества принадлежат различным полупространствам, и два подмножества называются отделимыми, если существует вектор .

1)

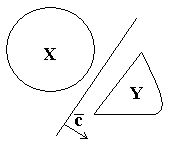
с – вектор нормали

2)

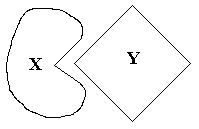
неотделимые

Теорема. Пусть даны два подмножества и . Тогда, если они:

1. не пересекаются,

2. оба выпуклы,

то они всегда отделимы.

Выпуклые функции и их свойства

Определение. Функция , определенная и конечная на выпуклом множестве называется выпуклой, если

(1)

– Неравенство Йенсена.

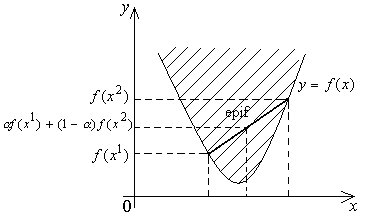
Геометрически неравенство Йенсена означает, что если взять любые две точки графика функции и соединить их хордой, то между этими точками график функций должен лежать ниже хорды.

Определение. Функция строго выпукла, если она выпукла и ее график не содержит прямолинейных отрезков.

– выпукла

– выпукла, но не строго

– строго выпукла

Определение. Функция называется вогнутой, если функция выпукла.

Критерии выпуклости:

1) выпукла в том и только в том случае, если ее график, т.е. является выпуклым подмножеством в .

2) Скалярный критерий выпуклости. Для того чтобы функция была выпукла, необходимо и достаточно, чтобы скалярная функция одной переменной была выпуклой.

3) Гладкий критерий выпуклости. выпукла в том и только в том случае, когда выполняется неравенство:

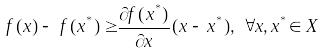(2)

4) Функция в классе выпукла в том и только в том случае, когда

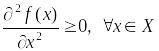(3)

5) Если функция , и (4) , то строго выпукла. Поскольку 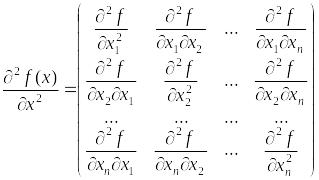, это –симметрическая матрица, то для проверки (3), (4) используются критерии Сильвестра неотрицательности и положительности квадратной матрицы.

Свойства выпуклых функций:

1. Выпуклая функция непрерывна в каждой своей внутренней точке и имеет в ней производные по любому направлению.

2. Если функция 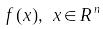выпукла, то ее множество уровня 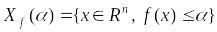для любого конечного числа 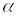является либо множеством выпуклым, либо пустым.

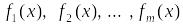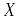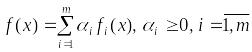3. Если функции выпуклы на , то и функция , то и функция 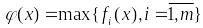является выпуклой.