5. Численное решение обыкновенных дифференциальных уравнений

5.1. Численные методы решения задачи Коши

Обыкновенными дифференциальными уравнениями (ОДУ) можно описывать задачи движения системы взаимодействующих материальных точек, химической кинетики, электрических цепей, сопротивления материалов (например, статический прогиб упругого стержня) и многие другие. Ряд важных задач для уравнений в частных производных также сводится к задачам для ОДУ. Так бывает, если многомерная задача допускает разделение переменных (например, задачи на нахождение собственных колебаний упругих балок и мембран простейшей формы). Таким образом, решение ОДУ занимает важное место среди прикладных задач физики, химии и техники.

Рассмотрим ОДУ первого порядка, записанное в общем виде:

. (5.1)

Общее решение (5.1) содержит произвольную константу С, т.е. является однопараметрическим семейством интегральных кривых . Для выбора конкретной интегральной кривой следует определить значение константы С, для чего достаточно задать начальные данные

y(x₀) = y₀. (5.2)

Несмотря на внешнюю простоту уравнения (5.1), решить его аналитически, т.е. найти общее решение с тем, чтобы затем выделить из него интегральную кривую , проходящую через точку , удается лишь для некоторых специальных типов уравнений. В общем случае решение задачи можно найти только приближенно.

Приближенное решение задачи (5.1), (5.2) будем искать на промежутке [x₀, x_n]. Построим расчетную сетку i = 1, 2,…,n, с шагом . Решение, найденное в узлах сетки y_i = y(x_i), занесем в таблицу

xi	x0	x1	…	xn
yi	y0	y1	…	yn

На каждом локальном интервале решение задачи представим в виде

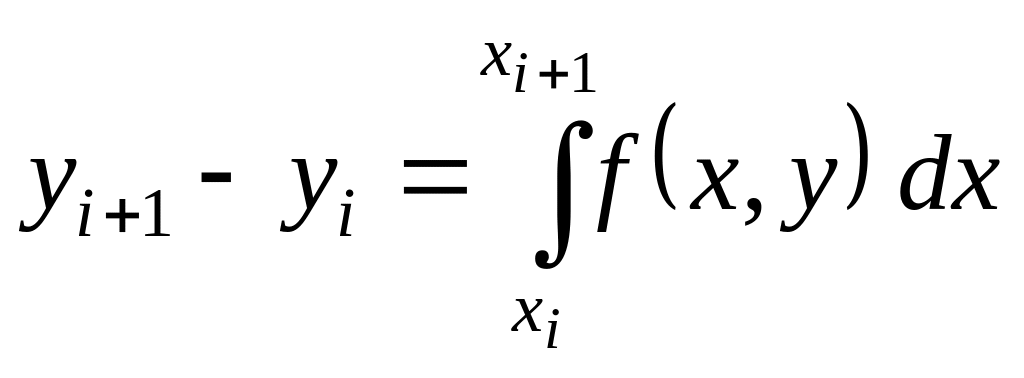. (5.3)

Заменим интеграл какой-либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка точности

,

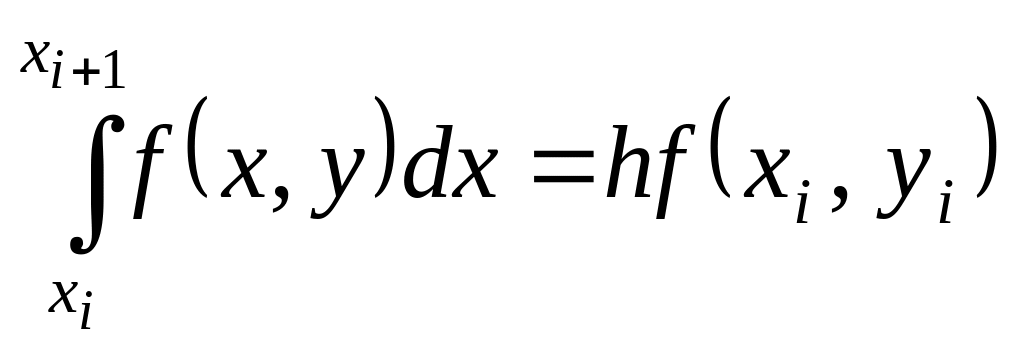то получим явную формулу Эйлера:

, . (5.4)

Если в (5.3) использовать формулу правых прямоугольников, то получим неявный метод Эйлера

, , (5.5)

в котором для вычисления неизвестного значения по известному значению требуется решать нелинейное уравнение.

Если для приближенного вычисления интеграла в (5.3) воспользоваться формулой средних прямоугольников

,

то получим метод предиктор–корректор:

,

. (5.6)

Метод (5.6) является частным случаем методов Рунге–Кутты:

, (5.7)

где

,

,

, (5.8)

,

…………………………………………….

.

Здесь _n, _nj, с_n, – параметры метода, которые выбираются из условия, чтобы метод имел максимально высокий порядок точности p. Можно показать, что p  q. Величины представляют собой правую часть уравнения при различных значениях аргументов. Их вычисление, занимающее основное расчетное время, называют этапом метода. Простейшим одноэтапным методом (q = 1) можно считать метод Эйлера. Наиболее распространенными являются методы Рунге–Кутты второго, третьего и четвертого порядка (т.е. двух-, трех- и четырехэтапные). При q = 2 получим однопараметрическое семейство двухэтапных методов Рунге–Кутты второго порядка аппроксимации:

,

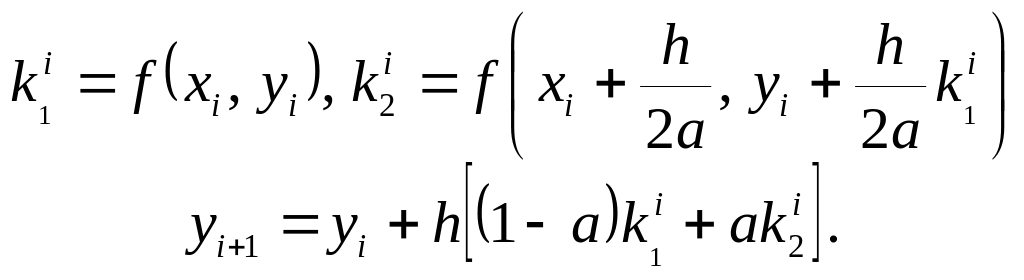При получаем формулы

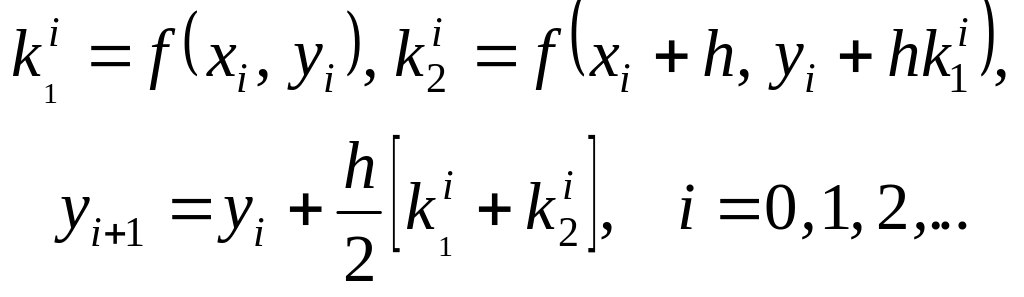(5.9)

При a = 1 получим метод, совпадающий с (5.7),

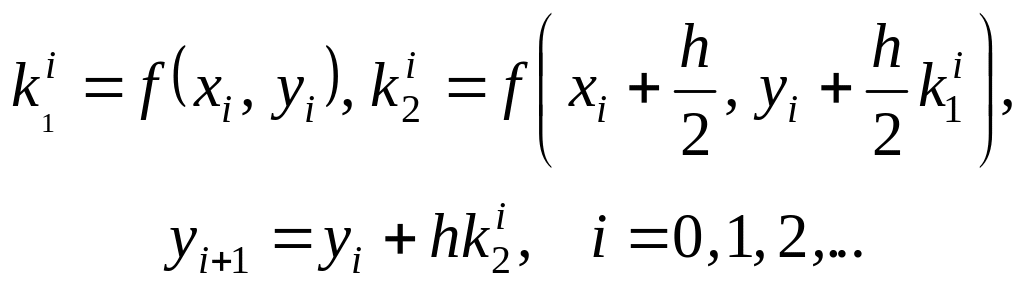
Приведем формулы трех- и четырехэтапных методов.

Трехэтапный метод Рунге–Кутты (вариант 1)

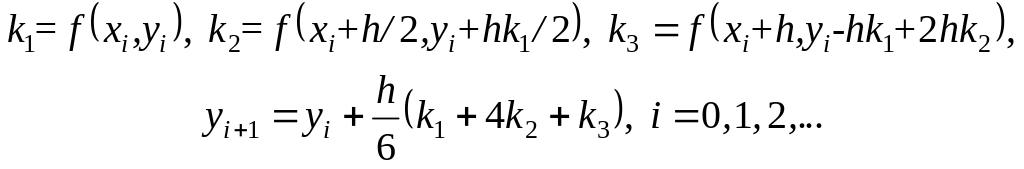(5.10)

Трехэтапный метод Рунге–Кутты (вариант 2)

(5.11)

Четырехэтапный метод Рунге–Кутты (вариант 1)

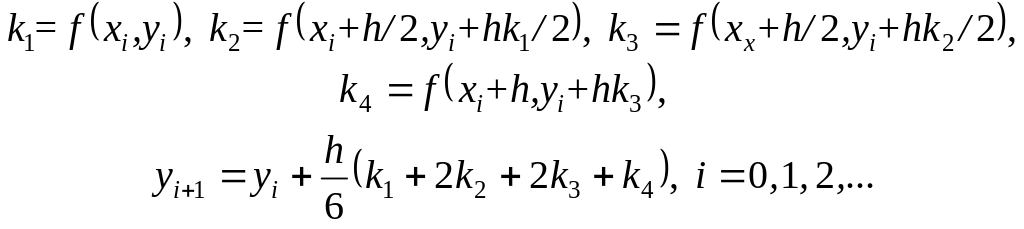(5.12)

Четырехэтапный метод Рунге–Кутты (вариант 2)

(5.13)

Численное решение систем ОДУ

Система ОДУ в общем виде может быть записана следующим образом:

. (5.14)

Поставим для (5.14) задачу Коши:

.

К решению задачи Коши для системы ОДУ сводится также задача Коши для ОДУ высших порядков

,

, , …,

путем замены переменных , k = 1, 2, …, n–1.

Для решения систем ОДУ полностью применимы все приведенные выше методы. Рассмотрим это на примере ОДУ второго порядка

, (5.15)

где u(t) – искомое решение; p(t), q(t), r(t) – заданные функции коэффициентов. Пусть для уравнения (5.15) поставлены начальные данные С помощью замены: v(t) = u(t), v(t) = u(t) уравнение сводится к системе:

,

где u(t),v(t) – искомые функции; g(t,u,v)  r(t) – p(t)v – q(t)u, f(t,u,v) v – функции правых частей; u⁰, v⁰– начальные данные.

Метод Эйлера легко обобщается на эту систему:

Здесь y_i, z_i – массивы приближенных решений для u, v соответственно, i = 1, 2,..., M. Решение находим по явным формулам:

y₀ = u⁰, z₀ = v⁰, y_i+1 = y_i+ f(t_i , y_i ,z_i), z_i+1 = z_i +  g(t_i, y_i, z_i). i = 1, 2,..., M.

Метод Рунге–Кутты (5.10) можно обобщить на систему следующим образом