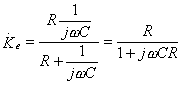- •1. Методы анализа электрических цепей постоянного тока.
- •2.Методы анализа электрических цепей переменного тока.
- •Метод комплексных амплитуд.
- •Уравнения линейного трансформатора.
- •Мощность цепи синусоидального тока и напряжения.
- •Баланс мощности в цепи синусоидального тока и напряжения.
- •3. Линейные цепи с несинусоидальными периодическими источниками
- •4. Анализ электрических цепей с многополюсными элементами.
- •Определение коэффициентов четырехполюсников.
- •Управляемые источники.
- •Индуктивно связанные ветви
- •Схемы замещения индуктивно сведённых ветвей в z параметрах с управляемыми источниками.
- •Частотные характеристики и передаточные функции четырехполюсников.
- •Анализ динамических режимов в линейных цепях.
- •Метод расчета нелинейных цепей.
Индуктивно связанные ветви
Индуктивно связанные ветви – две или более ветвей (катушек индуктивности) сцеплённых общим магнитным потоком.
L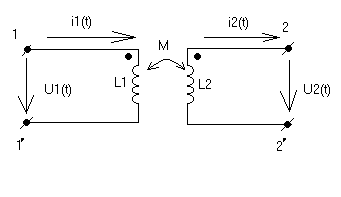 1-первичная,
L2
вторичная индуктивная обмотка.
1-первичная,
L2
вторичная индуктивная обмотка.
M – взаимная индуктивность
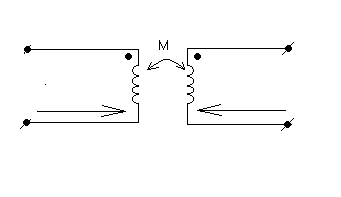
M>0
при согласном включении обмоток, токи
входят в одноименные зажимы соноправленно.

или
M<0 при встречном включении, токи входят в разноименные зажимы.

Запишем II закон Кирхгофа для первичной и вторичной обмотки.
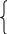
 для
1-ой обмотки
для
1-ой обмотки
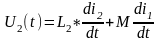 для
2-ой обмотки
для
2-ой обмотки
Будем считать что токи, магнитные потоки и напряжение изменяются по одному гармоническому закону, тогда запишем эти уравнения в комплексной плоскости:

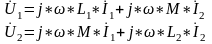

Z21=Z12 получим, что индукции сведённых ветвей имеют взаимную матрицу.
Схемы замещения индуктивно сведённых ветвей в z параметрах с управляемыми источниками.


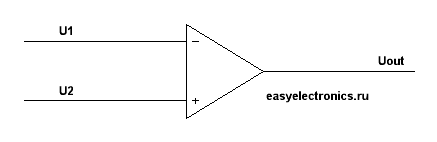
Операционный усилитель (ОУ) — усилитель постоянного тока с дифференциальным входом и, как правило, единственным выходом, имеющий высокий коэффициент усиления. ОУ почти всегда используются в схемах с глубокой отрицательной обратной связью, которая, благодаря высокому коэффициенту усиления ОУ, полностью определяет коэффициент передачи полученной схемы.
Uвых= K*Uвх а К в идеале равно бесконечности.
А входа два. И один из них прямой, а другой инверсный.
Более того, входы высокоомные. Т.е. их входное сопротивление равно бесконечности в идеальном случае и ОЧЕНЬ много в реальном. Счет там идет на сотни МегаОм, а то и на гигаомы. Т.е. оно замеряет напряжение на входе, но на него влияет минимально. И можно считать, что ток в ОУ не течет.
Напряжение на выходе в таком случае обсчитывается как:
|
Uout=(U2-U1)*K
Очевидно, что если на прямом входе напряжение больше чем на инверсном, то на выходе плюс бесконечность. А в обратном случае будет минус бесконечность.
Разумеется
в реальной схеме плюс и минус бесконечности
не будет, а их замещать будет максимально
высокое и максимально низкое напряжение
питания усилителя. И у нас получится:
Частотные характеристики и передаточные функции четырехполюсников.
Частотные характеристики и передаточные функции четырехполюсника. Реальные фильтры. Фильтры первого порядка. Частотные характеристики R-L-C цепей. Добротность R-L-C контура.
Пассивный
четырехполюсник представляет собой
электрическую цепь, внутри которой
имеется соединение элементов r, L и C.
Цепь имеет две пары зажимов: к первичным
зажимам подсоединяется источник энергии
(тока или напряжения), к вторичным зажимам
- нагрузка, под которой в общем случае
понимают пассивный или активный
двухполюсник с известными вольтамперными
характеристиками. На рис.1.1б изображена
комплексная схема замещения
четырехполюсника; на ней указаны токи
и напряжения входных и выходных зажимов
в виде комплексных переменных. Также
как и в двухполюснике, связь между этими
переменными может быть определена через
частотные характеристики четырехполюсника:
1. Входное сопротивление четырехполюсника
|
2. Входная проводимость четырехполюсника
|
|
3. Коэффициент передачи по напряжению
|
4. Коэффициент передачи по току
|
5. Передаточное сопротивление
|
6. Передаточная проводимость
|
|
Все эти формулы определяют причинно-следственную связь между заданным входным воздействием и реакцией цепи в виде тока или напряжения на входных или выходных зажимах. Также как и в двухполюсниках, все частотные характеристики не зависят от величин токов и напряжений, а определяются только параметрами элементов цепи и способом соединения ветвей. Они могут быть найдены опытным или расчетным путем. Все указанные выше характеристики называют внешними характеристиками четырехполюсника.
Некоторые из характеристик представляют собой частотную зависимость безразмерной величины, если сопоставляются колебания одной физической природы (напряжения с напряжением или тока с током), либо величины, имеющие размерность сопротивления [Ом] или проводимости [См]. Фазо-частотная характеристика - ФЧХ представляет собой зависимость разности фаз двух гармонических колебаний безотносительно к их физической природе. Эта разность может измеряться в градусах или в радианах.
Чтобы рассчитать комплексную передаточную функцию четырехполюсника в общем случае необходимо проделать следующее:
1.
Задаться произвольным значением ![]() или
или ![]() на
входе (обобщенная функция
на
входе (обобщенная функция ![]() ).
).
2.
Любым методом рассчитать комплексное
напряжение ![]() или
ток
или
ток ![]() на
выходе цепи (обобщенная функция
на
выходе цепи (обобщенная функция ![]() ).
).
3. Взять отношение выходного значения к входному. Входное значение при этом сокращается, получившееся выражение будет комплексной передаточной функцией, которую в общем случае обозначают буквой H(jω).
4. Получившееся комплексное выражение записать в показательной форме, для чего следует использовать формулы перехода от алгебраической формы записи комплексного выражения к показательной и обратно:
|
|
5. Сравнивая отдельно модули и фазы, выделить АЧХ и ФЧХ передаточной функции:
![]() -
АЧХ передаточной функции;
-
АЧХ передаточной функции;
![]() -
ФЧХ передаточной функции.
-
ФЧХ передаточной функции.
6. Изменяя значение переменной от 0 до бесконечности рассчитать и построить графики функций H(ω) и θ(ω). Целесообразно данные расчетов свести в таблицу, которую в дальнейшем можно использовать для анализа прохождения электрических сигналов через четырехполюсник.
Название фильтра |
Диапазон пропускаемых частот |
|||
Низкочастотный фильтр (фильтр нижних частот) |
|
|||
Высокочастотный фильтр (фильтр верхних частот) |
|
|||
Полосовой фильтр (полосно-пропускающий фильтр) |
|
|||
Режекторный фильтр (полосно-задерживающий фильтр) |
где |
К простейшим фильтрам первого порядка относятся цепочки, содержащие активные сопротивления и один реактивный элемент: емкость или индуктивность, включенные последовательно или параллельно.
Цепочки вида a), b), c), d) питаются от источника напряжения, а цепочки вида e) и f) – от источника тока.
Для определения фильтрующих свойств этих цепочек, запишем для каждой из них частотный коэффициент передачи, причем для цепочек a), b), c), d)
 ,
а для цепочек e), f)
,
а для цепочек e), f)![]()
 ,
,
![]() ,
, ![]() –
комплексные амплитуды входных напряжений
и тока,
–
комплексные амплитуды входных напряжений
и тока, ![]() -комплексная
амплитуда выходного напряжения.
Коэффициенты передачи определим для
случая холостого хода на выходе (
-комплексная
амплитуда выходного напряжения.
Коэффициенты передачи определим для
случая холостого хода на выходе (![]() ).
).
|
|
Обозначим
: RC=t ц,
L/R=t ц,
где t ц -
постоянная времени цепи, ![]() =
=![]() ,
где
-
граничная частота цепочки.
,
где
-
граничная частота цепочки.
Получаем
для цепочек a) и d) коэффициент передачи
вида:
для
цепочек b) и c):

и
для цепочек e) и f) соответственно :

Сравнивая соотношения для коэффициентов передачи всех цепочек, можно заметить, что все цепочки можно разделить на 2 вида, коэффициенты передачи которых можно записать следующим образом:

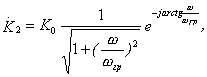
причем
в последовательных цепочках ![]() ,
а в параллельных
,
а в параллельных ![]() ,
,
Для
построения графиков АЧХ и ФЧХ и оценки
фильтрующих свойств цепочек первого
порядка рассмотрим следующие области
частот: область низких частот ![]() ,
область высоких частот
,
область высоких частот ![]() и
и ![]() .
.
Для первого типа цепочек имеем:
В
области низких частот ![]()
|
|||
|
|||
|
|
||
|
|
|
|
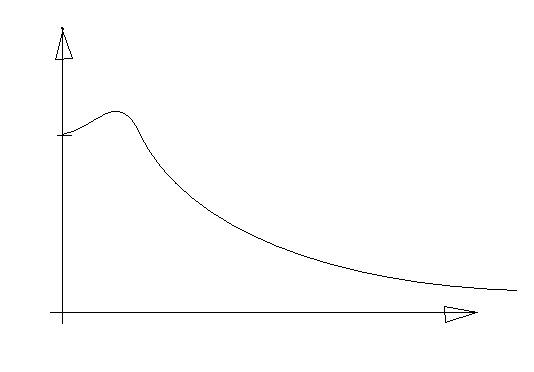
в области низких частот для первого типа цепочек (a, d, f) АЧХ линейно возрастает от нуля, а ФЧХ примерно равна p /2.
На частоте модуль коэффициента передачи
|
|
Отсюда и название этой частоты –“граничная”; эта частота определяет полосу пропускания фильтра по уровню K0/Ц2.
В области высоких частот
|
|
|
|
т.е.
в области высоких частот цепочки первого
типа имеют равномерную АЧХ, равную K0 ;
а у цепочки второго типа модуль АЧХ с
увеличением частоты изменяется по
закону ![]() ,
ФЧХ в этой области примерно равна -p /2.
На рис.7 представлены графики АЧХ и ФЧХ
обоих типов цепочек.
,
ФЧХ в этой области примерно равна -p /2.
На рис.7 представлены графики АЧХ и ФЧХ
обоих типов цепочек.

Добротность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.
Для Колебательного
контура в
RLC цепях:
![]() ,
где
,
где ![]() ,
, ![]() и
и ![]() — сопротивление, индуктивность и ёмкость резонансной
цепи, соответственно.
— сопротивление, индуктивность и ёмкость резонансной
цепи, соответственно.

Передаточная функция последовательного R-L-C контура.
Каноническая форма записи передаточной функции схемы 2-го порядка
H(p)=(b2*p2+b1*p+b0)/(p2+(0/Q)*p+0) p=j
ФНЧ, ФВЧ, ППФ, ПЗФ.
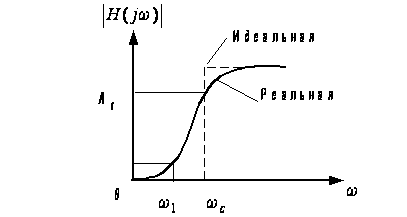
Фильтр нижних частот (ФНЧ) — один из видов аналоговых или электронных фильтров, эффективно пропускающий частотный спектр сигнала ниже некоторой частоты (частоты среза), и уменьшающий (подавляющий) частоты сигнала выше этой частоты. Степень подавления каждой частоты зависит от вида фильтра.

 -
Q>0,7
-
Q>0,7 -
Q<0,7
-
Q<0,7
Фильтр верхних частот (ФВЧ) — электронный или любой другой фильтр, пропускающий высокие частоты входного сигнала, при этом подавляя частоты сигнала ниже частоты среза. Степень подавления зависит от конкретного типа фильтра.

 -
Q<0,7
-
Q<0,7
 Q>0,7
Q>0,7
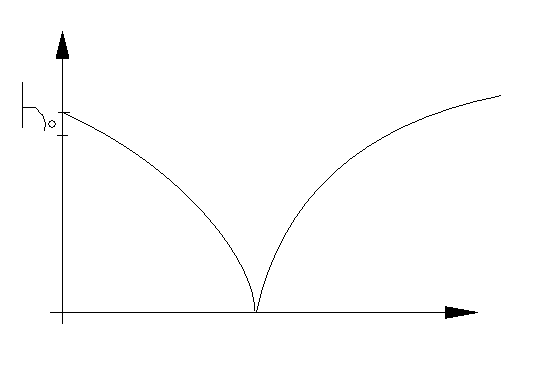
Полосно-пропускающий — фильтр, который пропускает частоты, находящиеся в некоторой полосе частот.


Полосно-заграждающий фильтр — электронный или любой другой фильтр, не пропускающий колебания некоторой определённой полосы частот, и пропускающий колебания с частотами, выходящими за пределы этой полосы.


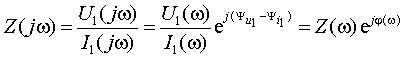







 ;
;