4. Анализ электрических цепей с многополюсными элементами.
Анализ электрических цепей с многополюсными элементами. Определение коэффициентов четырехполюсников. Уравнение типа Z. Уравнение типа Y, H – параметры, A – параметры. Пример T – образной схемы замещения. П – образная схема замещения.
Определение коэффициентов четырехполюсников.
1
4-х
полюсник
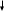
‘I’1
‘I’2
2
‘U’1 ‘U’2
1’ 2’
1) Уравнение типа “Z” (Z=[Ом])
Z11 Z12
‘
U’1=Z11’I’1+Z12’I’2
Z=
Z21
Z22
‘U’2=Z21’I’1+Z22’I’2
П
усть
сначала ‘I’2=0
(разомкнуты 2, 2’)
Z11=’U’1\’I’1 ||’I’2=0 –входное сопротивление при разомкнутых выходных зажимах.
Z21=’U’2\’I’1 ||’I’2=0 –взаимное сопротивление при разомкнутых выходных зажимах.
П усть ‘I’1=0 (разомкнуты 1, 1’)
Z22=’U’2 \’I’2 ||’I’1=0 –выходное сопротивление при разомкнутых входных зажимах.
Z12=’U’1\’I’2 ||’I’1 =0 –взаимное сопротивление при разомкнутых входных зажимах.
2) Уравнение типа “Y” (Y=[См])
‘ I’1=Y11’U’1+Y12’U’2
‘I’2=Y21’U’1+Y22’U’2
Y11 Y12
Y= Y21 Y22
3
) Уравнение типа “H”.
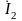
1
2
‘U’1=H11’I’1+H12’U’2
‘I’2=H21’I’1+H22’U’2
1’ 2’
Пусть сначала ’U’2=0
H11=’U’2\’I’1 ||’U’2=0 – входное сопротивление четырехполюсника при закороченных выходных зажимах.
H21=’I’2\’I’1 ||’U’2=0 – коэффициент передачи по току при закороченных выходных зажимах.
H22=’I’2\’U’1 ||’I’2=0 – выходная проводимость при разомкнутых входных зажимах .
H12=’U’1\’U’2 ||’I’1=0 – коэффициент передачи по напряжению при разомкнутых входных зажимах.
4) Уравнение типа “A”
‘U’1=A’U’1+B’I’2
‘
I’1=C’U’2+D’I’2
‘I’1
‘I’2
A B
A= C D
Схемы замещения четырехполюсников.
1) T-образная схема.
‘I’1
‘I’2
‘U’1
Z1
Z2
‘U’2
Z3 взаимный четырехполюсник
Н айдем Z для T образной схемы.
‘U’1=Z11’I’1+Z12’I’2
‘U’2=Z21’I’1+Z22’I’2
Пусть 2. 2’ разомкнуты -‘I’2=0
Z11=’U’1\’I’1 ||’I’2=0 –входное сопротивление
Z21=’U’2\’I’1 ||’I’2=0=(’I’1 Z3)\ ’I’1=Z3
П
усть
‘I’1=0
(разомкнуты
1, 1’) Z12=Z21
взаимный четырехполюсник
Z22=’U’2 \’I’2 ||’I’1=0 –выходное сопротивление
Z12=’U’1\’I’2 ||’I’1 =0=(’I’2 Z3)\ ’I’2=Z3
2) П-образная схема.
‘ I’1 ‘I’2
Z1
‘U’1 Z2 Z3 ‘U’2
‘U’1=H11’I’1+H12’U’2
‘I’2=H21’I’1+H22’U’2
Проведем опыт К.З. на входе --’U’2=0
Каскадное соединение четырехполюсников. Управляемые источники (УИ). Схема замещение четырехполюсников с УИ. Индуктивно-связанные ветви. Схема замещения индуктивно-связанных ветвей с УИ в Z – параметрах. Операционный усилитель (ОУ). Идеальный ОУ.
Каскадное
‘
A1 B1
C1 D1
A2 B2
C2 D2
I’1
=’I’11
‘I’21=’I’12
‘I’2=’I’22
‘U’1=’U’11 ‘U’12=’U’21 ‘U’22=’U’2
При этом используется уравнение типа ”A”
‘ U’11=A1’U’21+B1’I’21 ‘U’12=A2’U’22+B2’I’22=‘U’21
‘I’11=C1’U’21+D1’I’21 ‘I’12=C2’U’22+D2’I’22=‘I’21
’U’1 ‘U’11 A1 B1 ’U’21 A1 B1 A2 B2 ’U’22
’I’1 = ‘I’11 = C1 D1 ’I’21 C1 D1 C2 D2 ’I’22 =
A1 B1 A2 B2
A= C1 D1 X C2 D2 = A1 B1 A2 B2 ’U’2
C1 D1 C2 D2 ’I’2