3. Линейные цепи с несинусоидальными периодическими источниками
Разложение периодических функций в ряд Фурье. Применение принципа суперпозиции и метод комплексных амплитуд при действии источников постоянного тока и каждого из гармонических источников.
На практике ЭДС и токи в большей или меньшей степени являются несинусоидальными. Это связано с тем, что реальные генераторы не обеспечивают, строго говоря, синусоидальной формы кривых напряжения, а с другой стороны, наличие нелинейных элементов в цепи обусловливает искажение формы токов даже при синусоидальных ЭДС источников.
На практике к несинусоидальности напряжений и токов следует подходить двояко:
в силовой электроэнергетике несинусоидальные токи обусловливают в общем случае дополнительные потери мощности, пульсации момента на валу двигателей, вызывают помехи в линиях связи; поэтому здесь необходимо «всеми силами» поддержание синусоидальных режимов;
в цепях автоматики и связи, где несинусоидальные токи и напряжения лежат в основе принципа действия электротехнических устройств, задача наоборот заключается в их усилении и передаче с наименьшими искажениями.
В общем случае характер изменения величин может быть периодическим, почти периодическим и непериодическим. В данном разделе будут рассматриваться цепи только с периодическими переменными.
Периодическими несинусоидальными величинами называются переменные, изменяющиеся во времени по периодическому несинусоидальному закону. Причины возникновения несинусоидальных напряжений и токов могут быть обусловлены или несинусоидальностью источника питания или (и) наличием в цепи хотя бы одного нелинейного элемента. Кроме того, в основе появления несинусоидальных токов могут лежать элементы с периодически изменяющимися параметрами.
В качестве примера на рис. 1,а представлена цепь с нелинейным резистором (НР), нелинейная вольт-амперная характеристика (ВАХ) которого обусловливает несинусоидальную форму тока i в цепи при синусоидальном напряжении u на ее входе (см. рис. 1,б).
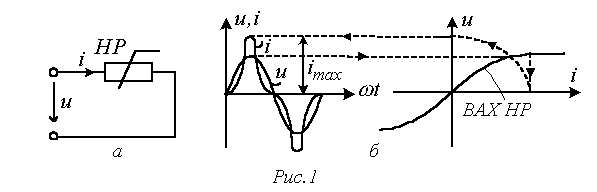
Характеристики несинусоидальных величин
Для характеристики несинусоидальных периодических переменных служат следующие величины и коэффициенты (приведены на примере периодического тока):
Максимальное значение -
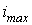.Действующее значение -
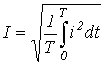.Среднее по модулю значение -
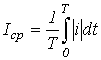.Среднее за период значение (постоянная составляющая) -
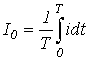.Коэффициент амплитуды (отношение максимального значения к действующему) -
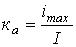.Коэффициент формы (отношение действующего значения к среднему по модулю) -
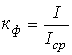.Коэффициент искажений (отношение действующего значения первой гармоники к действующему значению переменной) -
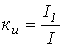.Коэффициент гармоник (отношение действующего значения высших гармонических к действующему значению первой гармоники) -
.
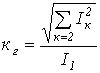Разложение периодических несинусоидальных кривых в ряд Фурье
Из
математики известно, что всякая
периодическая функция 
,
где Т – период, удовлетворяющая условиям
Дирихле, может быть разложена в
тригонометрический ряд. Можно отметить,
что функции, рассматриваемые в
электротехнике, этим условиям
удовлетворяют, в связи с чем проверку
на их выполнение проводить не нужно.
При разложении в ряд Фурье функция представляется следующим образом: |
(1) |
.
Здесь 
-
постоянная составляющая или нулевая
гармоника; 
-
первая (основная) гармоника, изменяющаяся
с угловой частотой 
,
где Т – период несинусоидальной
периодической функции.
В
выражении (1) 
,
где коэффициенты 
и 
определяются
по формулам
;
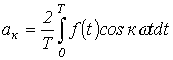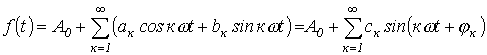