
- •1. Методы анализа электрических цепей постоянного тока.
- •2.Методы анализа электрических цепей переменного тока.
- •Метод комплексных амплитуд.
- •Уравнения линейного трансформатора.
- •Мощность цепи синусоидального тока и напряжения.
- •Баланс мощности в цепи синусоидального тока и напряжения.
- •3. Линейные цепи с несинусоидальными периодическими источниками
- •4. Анализ электрических цепей с многополюсными элементами.
- •Определение коэффициентов четырехполюсников.
- •Управляемые источники.
- •Индуктивно связанные ветви
- •Схемы замещения индуктивно сведённых ветвей в z параметрах с управляемыми источниками.
- •Частотные характеристики и передаточные функции четырехполюсников.
- •Анализ динамических режимов в линейных цепях.
- •Метод расчета нелинейных цепей.
Уравнения линейного трансформатора.
Пусть i1, i2 — мгновенные значения тока в первичной и вторичной обмотке соответственно, u1 — мгновенное напряжение на первичной обмотке, RH — сопротивление нагрузки. Тогда
![]()
![]()
Здесь L1, R1—
индуктивность и активное сопротивление
первичной обмотки, L2, R2—
то же самое для вторичной обмотки, L12—
взаимная индуктивность обмоток. Если
магнитный поток первичной обмотки
полностью пронизывает вторичную, то
есть если отсутствует поле рассеяния,
то ![]() .
Индуктивности обмоток в первом приближении
пропорциональны квадрату количества
витков в них.
.
Индуктивности обмоток в первом приближении
пропорциональны квадрату количества
витков в них.
Последовательное соединение катушек с взаимной индукцией.
Пусть две катушки, обладающие сопротивлениями R1 и R2 , индуктивностями L1 и L2 и взаимной индуктивностью M, соединены последовательно.

Возможны два вида их соединения – согласное и встречное (а.б). При согласном ток одновременно входит или выходит из катушек. При встречном ток из одной катушки выходит, а в другую входит.
Напряжение на каждой из катушек содержит три составляющих: падение напряжения на активном сопротивлении, напряжение самоиндукции и напряжение взаимной индукции:

Последние имеют одинаковые знаки при согласном включении и разные при встречном. Напряжение на входе цепи равно сумме этих двух напряжений:
![]()
Входное комплексное сопротивление цепи получим из совместного рассмотрения трех последних уравнений:
![]()
где Z1 и Z2 – комплексные сопротивления катушек, а ZM – комплексное сопротивление взаимной индукции:

Мощность в цепи синусоидального тока. Баланс мощностей цепи синусоидального тока. Передача мощности от активного двухполюсника к пассивному двухполюснику.
Мощность цепи синусоидального тока и напряжения.
Мгновенная мощность:
P(t)=U(t)*i(t)
U(t)=Umax*sin(ωt+ψu)
i(t)=Imax*sin(ωt+ψi)
P(t)=Umax*Imax*sin(ωt+ψu)*sin(ωt+ψi)= *[cos(ψu-
ψi)-cos(2ωt+
ψu+
ψi)]
*[cos(ψu-
ψi)-cos(2ωt+
ψu+
ψi)]
ψu - ψi=φ
А ктивная
мощность - средняя за период.
0
ктивная
мощность - средняя за период.
0
P=
=
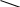


P=U*I*cos(φ) [Вт]
Реактивная мощность:
Q=U*I*sin(φ) [ВАР] – вольт-ампер реактивная
Комплексная мощность:
S̃= *
=U*ejψu
*
I * e-jψI=U*I*ej(ψu
- ψI)=U*I*ejφ=
*
=U*ejψu
*
I * e-jψI=U*I*ej(ψu
- ψI)=U*I*ejφ=
=U*I*cos(φ)+j*U*I*sin(φ)=P+jQ
S̃=[Вольт Амперы]
S – полная мощность
S=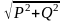 =UI
=UI
Рассмотрим z=r±jx
Если
z=r,
тогда P=
Если
z=jx,
тогда P=0;
S̃=P+jQ=jωL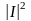
ZL → Q>0
Если
z=-jx,
тогда P=0;
S̃=-j*
ZC → Q<0
Баланс мощности в цепи синусоидального тока и напряжения.
 =0;
=0;
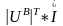 в
в

S ̃=
̃= *
k
*
k
 S̃k=0
Сумма комплексных мощностей всех
ветвей схемы равна нулю
S̃k=0
Сумма комплексных мощностей всех
ветвей схемы равна нулю

 *
=0
- теорема Теллегена
*
=0
- теорема Теллегена
Докажем что сумма мощностей отдаваемая источниками равна сумме мощностей потребляемых цепью.

k=
zk-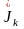
=
zk*zk-
Uk*
k=Uk*(
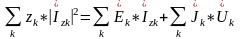


S̃потр. S̃ист.
S̃E
= S̃J=
S̃J=
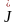
S̃потр=(r+jx)*
 =r*
+jx*
=Pпотр+jQпотр
=r*
+jx*
=Pпотр+jQпотр
S̃ист=Pист+jQист

S̃ист= S̃потр Баланс мощности
Передача
мощности от активного двухполюсника
к п ассивному
в цепях синусоидального тока и напряжения.
ассивному
в цепях синусоидального тока и напряжения.
I zвх






А U П Ep zн=R+jx
Zвх=rвх+jxвх
Zн=rн+jxн
P=zн*
;
=

Максимальная мощность:
1)
xн=
-xвх
;

2) rн=rвх ; zн=rвх-jxвх
