ТОЭ

1. Методы анализа электрических цепей постоянного тока.

Основные определения. Классификация цепей. Основные задачи теории цепей. Основные интегральные переменные. Математические модели двухполюсных элементов цепи (во временной области). Независимый идеальный источник ЭДС (напряжения). Независимый идеальный источник тока. Обобщенная ветвь цепи. Топологические уравнения.

5 видов классификаций ЭЦ: системные связи, компьютерные, системы контроля, сигналопередающие, энергетические.

ЭЦ – совокупность связанных между собой компонентов предназначенная для генерации, передачи, потребления и преобразования электрической энергии и информации.

Классификация цепей.

1. По назначению: энергетические, информационные.

2. По виду сигнала: аналоговые (основные параметры (ток, заряд..) являются непрерывными функциями времени), дискретные (основные переменные отличаются от нуля в определенный (дискретный) момент времени).

3. По типу параметров ЭЦ:

Цепи с сосредоточенными параметрами, процессы в которых являются функциями времени и не зависят от координаты.	Цепи с распределенными параметрами, зависят не только от времени, но и от координаты.
Линейные, параметры не зависят от тока и напряжения.	Нелинейные, зависят от тока и напряжения.

Схема замещения ЭЦ – математическая модель реальных устройств, которая учитывает физические процессы, происходящие в реальных условиях. Схемы замещения отображают свойства ЭЦ при определенных условиях.

Теория цепей имеет два направления:

• анализ электрических цепей

• синтез (создания новых) электрических цепей.

Анализ – реакция при заданных входных параметрах (известно: Uвх, параметры схемы, и способ соединения элементов; определить: Uвых).

Синтез – построить цепь по входному воздействию (известно Uвх, Uвых; определить: схему).

Основные интегральные переменные:

U(t) – напряжение (U(t)=φ1- φ2), [В]

i(t) – ток ( ), [А]

P(t) – мощность (P(t)= U(t)* i(t)), [Вт], P(t)>0 – энергия поглощается, P(t)<0 – отдает.

W(t) – энергия ( W= ∫U(t)*I(t)dt.), [Дж].

Математическая модель – совокупность уравнений описывающих процессы в данной ЭЦ.

Компонентные уравнения – описывают компоненты из которых состоит цепь и не зависят от способа их соединения.

Топологические уравнения – описывают способ соединения элементов и не зависят от самих элементов.

Компоненты: пассивные, активные.

Математические модели двухполюсных элементов цепи (во временной области):

1. Резистивный элемент.

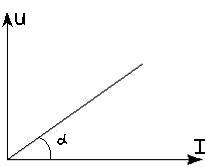  - ВАХ

U(t)=i(t)*R –компонентное уравнение для резистивного элемента.

G = 1 / R – проводимость [См].

Резистор потребляет энергию. P(t) =U(t)*i(t)=R* .

2. Индуктивный элемент.

ψ(i) – поток сцепления [Вб/А].

Ф – поток.

Вебер Амперная характеристика ψ = w*Ф, ψ = L*i, (w – количество витков, L – индуктивность [Гн]).

Для линейных цепей: - компонентное уравнение для индуктивности.

3. Емкостной элемент.

Кулон Вольтная характеристика (КВХ) - q(u) запасает энергию поля.

-компонентное уравнение для конденсатора.

Источник ЭДС (идеальный источник напряжения) — двухполюсник, напряжение на зажимах которого постоянно (не зависит от тока в цепи). U(t)=E(t), r(вн)=0.

Идеальный источник тока (источник тока) - это идеализированный активный элемент, ток которого не зависит от напряжения на его зажимах. Ток источника i(t) = J.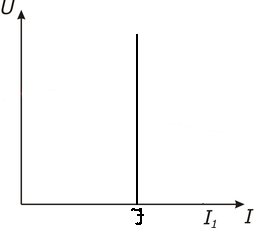 

Обобщенная ветвь цепи.

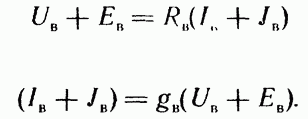
Топологические уравнения.

Ветвь – участок электрической цепи с одним и тем же током.

Узел – место соединения трех и более ветвей.

Контур – замкнутый путь состоящий из нескольких ветвей цепи. Ни ветви, ни узлы в контуре не повторяются.

1. Алгебраическая сумма токов ветвей соединенных в узле равна 0, .

Токи отходят – «+», токи входят – «-».

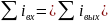
2. Алгебраическая сумма напряжений ветвей образующих контур равна 0 для любого момента времени.

, где – S число ветвей в контуре.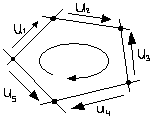

Основные принципы и теоремы теории электрических цепей. Принцип суперпозиции (метод наложения). Определение коэффициентов метода наложения. Способ расчета цепи с помощью метода наложения.

Теорема наложения (суперпозиции), взаимности (обратимости), компенсации, об эквивалентном источнике (эквивалентном генераторе).

Принцип компенсации:

Токи в ветвях схемы не изменятся, если ветвь с током i заменить источником тока J с током i или ветвь с напряжением U заменить источником ЭДС E.

Об эквивалентном источнике (эквивалентном генераторе):

Любая линейная активная цепь по отношению к произвольной ветви может быть представлена, как активный двухполюсник схемой Нортона или Тевеннена, с параметрами Uр, Iкз, Rвх.

Принцип суперпозиции (метод наложения):

Реакция линейной цепи при одновременном действии независимых источников равна алгебраической сумме реакций при действии каждого источника в отдельности.

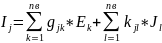
Определение коэффициентов метода наложения:

,

, все 0, кроме

Способ расчета цепи с помощью метода наложения.

Метод наложения состоит: в замене одной схемы с n источниками ЭДС и (или) тока n такими же схемами, с одним источником в каждой; расчет отдельных токов в ветвях цепи с одним источником и их алгебраическом сложении для определения токов заданной цепи с n источников.

При выключении источника ЭДС электрическая цепь закорачивается, поскольку ее Rвн = 0, а источники тока – разрывается, поскольку их Rвн → ∞.

Принцип компенсации. Теорема об активном двухполюснике (метод эквивалентного генератора). Узловые уравнения электрической цепи. Составление узловых уравнений непосредственно по схеме.

Принцип компенсации:

Токи в ветвях схемы не изменятся, если ветвь с током i заменить источником тока J с током i или ветвь с напряжением U заменить источником ЭДС E.

Об активном двухполюснике (эквивалентном генераторе):

Любая линейная активная цепь по отношению к произвольной ветви может быть представлена, как активный двухполюсник схемой Нортона или Тевенина, с параметрами Uр, Iкз, Rвх.

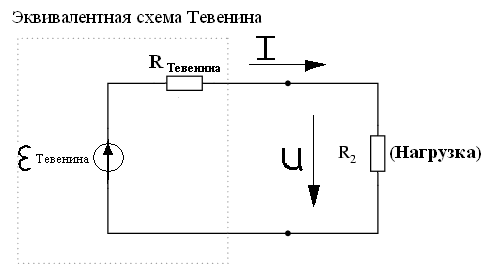
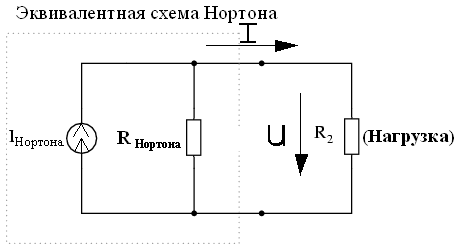
U=Eразр-Rтевенина*I I=Iкз-U/Rнортона

Узловые уравнения можно получить, если в уравнения Кирхгофа подставить компонентные уравнения. В результате получим систему из ( уравнений с неизвестными потенциалами.

Передача электрической энергии от активного двухполюсника к пассивному двухполюснику. Баланс мощностей в электрической цепи. Узловые уравнения электрической цепи.

Передача энергии от активного двухполюсника (источника) к пассивному двухполюснику (приемнику)

Двухполюсником называется устройство или часть схемы (цепи) с двумя выводами (полюсами). Если внутри двухполюсника содержатся источники энергии, то он называется активным (A), в противном случае – пассивным (П).

Энергетические характеристики передачи энергии от активного двухполюсника (источника) к пассивному двухполюснику (приемнику) на переменном токе зависят от соотношения параметров приемника и источника между собой.

Баланс мощностей в электрической цепи - в любой электрической цепи сумма мощностей всех источников электрической энергии должна быть равна сумме мощностей всех приемников и вспомогательных элементов.

PИ = n m   k = 1   Uk * Jk +     k = 1   Ek * Ik

Должны быть учтены как внешние резисторы, так и внутренние сопротивления самих источников.

Узловые уравнения электрической цепи.

Формула 2ух узлов: