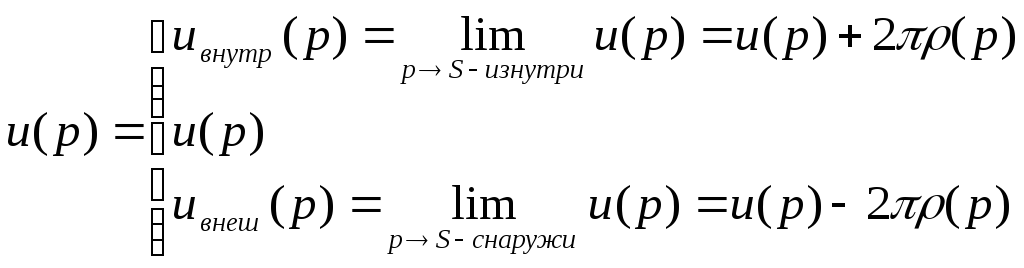- •Оглавление
- •Первая и вторая формулы Грина с оператором, следствия.
- •Гармонические функции. Интегральное представление. Их основные свойства.
- •Примеры
- •Свойства гармонических функций.
- •Теорема о среднем для гармонических функций
- •Теорема о максимумах и минимумах для гармонических функций. Единственность и корректность задач Дирихле.
- •Следствия:
- •Функция Грина для краевой задачи с уравнением Пуассона. Её построение методом отображений.
- •Функция Грина для задачи с уравнением, понятия, определения.
- •Решение задач с её помощью
- •Построение функции Грина в одномерном случае на отрезке
- •Теория потенциалов, определение, основные свойства.
- •Объёмный потенциал
- •Потенциал простого слоя
- •Потенциал двойного слоя
- •Решение задач Дирихле с уравнением Пуассона методом теории потенциалов
- •Сводная таблица6 общие сведения о потенциалах:
- •Понятие о корректно и некорректно поставленных задачах математической физики, примеры.
- •Уравнение с операторомс особенностью, свойства, ограниченность, постановка задачи.
- •Уравнение Бесселя.
- •Особенность, построение ограниченного решения .
- •Общее решение, ,,,понятие о функциях .
- •Асимптотика решений уравнения Бесселя, нули функции Бесселя.
- •Краевая задача на собственные значения: ,её решение, ортогональность собственных функций, теорема Фурье-Бесселя б/д.
- •Модифицированное уравнение Бесселя, ограниченность решения , свойства, общее решение, понятие о функции .
- •Сводная таблица.
- •Краевая задачас двумя особыми точками на концах отрезка. Граничные условия. Условия самосопряжённости оператора.
- •Уравнение гипергеометрического типа.
- •Приведение к самосопряжённому виду. Весовые функции . Уравнение для производных(в следующем пункте).
- •Решение в виде полиномов. Формула Родрига.
- •Ортогональные решения полиномов. Свойства нулей.
- •Примеры: уравнения, краевые задачи, определение и свойства полиномов
- •Полиномы Лежандра.
- •Полиномы Чебышева-Лягера.
- •Чебышева-Эрмита.
- •Сводная таблица для уравнений гипергеометрического вида.
- •Уравнения, краевая задача для присоединенных полином Лежандра. Решения. Основные свойства.
- •Уравнение Лапласа в сферических координатах. Схема решения методом разделения переменных.
- •Сферические функции, определения, построение системы базисных функций. Ортогональность, полнота, теорема о разложении, б/д.
Решение задач Дирихле с уравнением Пуассона методом теории потенциалов
Полученные свойства потенциалов позволяют пользоваться ими как удобным аппаратом для решения краевых задач.
Решим первую краевую задачу с уравнением Пуассона.
Задача:
найти функцию, гармоническую в области
![]() ,
ограниченную контуром
,
ограниченную контуром![]() и удовлетворяющую на
и удовлетворяющую на![]() граничным условиям. Рассмотрим первую
краевую задачу: (1)
граничным условиям. Рассмотрим первую
краевую задачу: (1)![]() ,
ищем
,
ищем![]() ,
дважды дифференцируемую и непрерывную
в
,
дважды дифференцируемую и непрерывную
в![]() ,
удовлетворяющую уравнению и начальным
условиям.
,
удовлетворяющую уравнению и начальным
условиям.
Объёмный
потенциал
![]() :
внутри области
:
внутри области![]() имеетII
производную и:
имеетII
производную и:
![]() ,
пусть
,
пусть![]()
![]()
![]() ,
,![]() .
.
Пусть
![]() ,
причём, для
,
причём, для![]() задача будет ставиться следующим
образом: (2)
задача будет ставиться следующим
образом: (2)![]() ,
задачу (1) свели к (2). Ищем её решение в
виде потенциала двойного слоя:
,
задачу (1) свели к (2). Ищем её решение в
виде потенциала двойного слоя:![]() ,
она удовлетворяет уравнению и граничному
условию (2). Таким образом, получили
уравнение, которому удовлетворяет
,
она удовлетворяет уравнению и граничному
условию (2). Таким образом, получили
уравнение, которому удовлетворяет![]() :
:![]() ,
из этого уравнения надо найти плотность
,
из этого уравнения надо найти плотность![]() .
.
Таким образом, решением краевой задачи будет потенциал двойного слоя с плотностью, удовлетворяющей последнему уравнению.
Сводная таблица6 общие сведения о потенциалах:
|
Потенциал |
Объёмный потенциал |
Потенциал простого слоя |
Потенциал двойного слоя |
|
Физическая интерпретация |
Объём
|
В
объёме Д находится заряженный непрерывно
с плотность
|
В
объёме Д находятся два непрерывно
зараженных с плотность момента диполей
|
|
Вид потенциала |
|
|
|
|
|
Если
| ||
|
|
Если
| ||
|
|
|
|
|
|
Первые производные: |
|
величины разрыва (производная рвётся) |
Говорить о них нельзя |
|
Дополнительно: |
Вторые
производные:
|
|
Если
поверхность S
замкнута, и нормаль направлена внутрь,
то можно указать величину разрыва:
|
|
В
2D
случае всё аналогично, нужно сделать
лишь следующие замены:
| |||
Понятие о корректно и некорректно поставленных задачах математической физики, примеры.
Корректность
- непрерывная зависимость решения от
дополнительных условий в любой конечной
точке области, т.е. если имеем уравнение
![]() и два условия
и два условия![]() ,
причём
,
причём![]() (отличные на малую величину), то и
(отличные на малую величину), то и![]() (тоже мало отличаются).
(тоже мало отличаются).
Пусть
![]() ,
,![]() -
гармоническая функция, тогда:
-
гармоническая функция, тогда:![]()
![]() ,
тогда по теореме о максимумах и минимумах
везде в областиD
верно:
,
тогда по теореме о максимумах и минимумах
везде в областиD
верно:
![]()
![]()
![]() то есть малому изменению граничных
условий отвечает малое изменение
решений. Задача Дирихле корректна.
то есть малому изменению граничных
условий отвечает малое изменение
решений. Задача Дирихле корректна.
Пример
некорректной задачи:
![]() -
уравнение Лапласа. Рассмотрим задачу
Коши:
-
уравнение Лапласа. Рассмотрим задачу
Коши: .
.
Рассмотрим
два типа начальных условий:
 .
Эти граничные условия мало отличаются
при
.
Эти граничные условия мало отличаются
при![]() .
Но решения не будут близкими при этом:
.
Но решения не будут близкими при этом: ,
т.к.
,
т.к.![]() .
Таким образом, решения будут существенно
различны.
.
Таким образом, решения будут существенно
различны.
Уравнение с операторомс особенностью, свойства, ограниченность, постановка задачи.
Теория
специальных функция – это теория
следующих уравнений: (*)![]() - линейное дифференциальное уравнение
второго порядка. Пусть функция
- линейное дифференциальное уравнение
второго порядка. Пусть функция![]() ,
т.е.
,
т.е.
![]() -
нуль первого порядка. Решение (*) всегда:
-
нуль первого порядка. Решение (*) всегда:![]() .
Рассмотрим решение в окрестности особой
точки, в которой
.
Рассмотрим решение в окрестности особой
точки, в которой
![]() обращается в ноль.
обращается в ноль.
Теорема.
Если уравнение
![]() имеет ограниченное в точке
имеет ограниченное в точке![]() решение
решение![]() ,
то все остальные решения
,
то все остальные решения![]() (линейно независимые) не ограничены:
(линейно независимые) не ограничены:![]() .
То есть существует одно ограниченное
решение.
.
То есть существует одно ограниченное
решение.
Доказательство:
Из теории ОДУ знаем, что
![]() ,
,![]() -
Вронскиан двух решений. Докажем:
-
Вронскиан двух решений. Докажем:![]() ,
тогда
,
тогда ,
чтд.
,
чтд.
У
нас
![]() ограничено, а
ограничено, а![]() - нет. Рассмотрим следующую величину:
- нет. Рассмотрим следующую величину: .
Проинтегрируем эту величину:
.
Проинтегрируем эту величину:
![]()
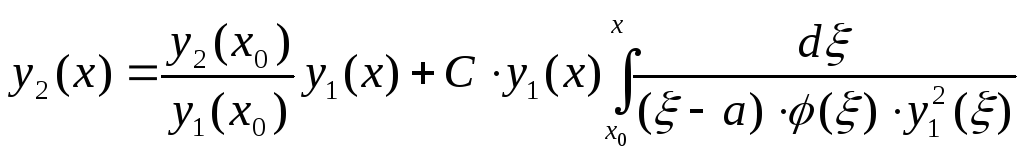 ,
, ,
следовательно, этот интеграл расходится
при
,
следовательно, этот интеграл расходится
при
![]() ,
а это значит, что
,
а это значит, что![]() ,
чтд.
,
чтд.
Уточним теорему: рассмотрим два случая.
1.
![]() в окрестности точки
в окрестности точки![]() ,
,![]() ~
~![]() ,
т.е.
,
т.е.
![]() как логарифм.
как логарифм.
2.
![]() ~
~ ~
~![]() - полюс порядка
- полюс порядка![]() .
.
Проанализируем получившееся решение:
|
|
Если
требуется ограниченное решение в
особой точке, то
Так как полное решение (*) всегда является суммой двух решений: ограниченного и неограниченного, то ограниченность этого первого решения уже есть само по себе граничное условие. |