Билеты по уравнениям математической физики / экзамен 5-ый семестр / экзамен по урматам2

9.Уравнение теплопроводности. Физический смысл.

Выведем уравнение, описывающие распределение температуры в теле. Пусть - температура тела в точке М в момент времени t. Будем пользоваться законом Фурье для плотности потока тепла ω в направлении в единицу времени: , к – коэффициент теплопроводности, может зависеть от температуры, точки и времени. Рассмотрим часть тела D, ограниченную поверхность S. Пусть - плотность источников тепла. подсчитаем баланс тепла для D за малое время Δt: Q₁=Q₂+Q₃, где

- приход за счёт источников тепла.

- расход за счёт выходящего из D потока.

- расход на изменение температуры, где с – коэффициент теплоёмкости, ρ – плотность в-ва.

Тогда можно записать: , откуда ввиду произвольности D следует:

- уравнение теплопроводности.

10. Задача Коши с однородным уравнением на прямой

а.Решение с точечным источником.

Решение:, прокомментируем результат: в формуле участвует суммирование по “n” и интегрирование по Д, переставим их: ,

- ядро, функция Грина (функция источника) задачи.

Получим вид функции Грина:

Есть задача:

Рассмотрим частный случай: решение этой задачи:

Проведём замену, при такой замене вид задачи не изменится: , где

Тогда для функции υ можно записать выражение: ,т.е. получили функцию одной переменной , решение свелось к решению для функции одной переменной .

Подставляем:

Интегрируем: , =0, т.к. задача симметрична относительно ξ , чётная функция => производная равна нулю.

Интегрируем: , выбираем из условия: , интегрируем, , значитпостоянен во времени.

Прокомментируем полученный результат: чтобы понять, что такое функция Грина, рассмотрим следующую задачу:

возьмём временно сосредоточенной в некоторой точке р0. Пусть временно: и в этом случае решение примет вид:

т.е. то решение задачи ) в т. . При

в.Построение решения с известной функцией Грина.

Рассмотрим задачу:

её решение:

Рассмотрим это решение: следовательно это решение удовлетворяет уравнению . следовательно это решение удовлетворяет начальным условиям.

Рассмотрим частные случае:

Лемма1: , если - продлеваем нечётным образом, то решение задачи Коши: - интеграл от нечётной функции в симметричных пределах.

Лемма2: , если , то

Можно записать для задачи 1:

, и т.д.

с.Функция Грина в двумерном и трехмерном случаях.

трёхмерная задача Коши с постоянными коэффициентами:

Лемма: если , то - каждое является решением одномерной задачи Коши с соответств. начальными данными.(доказывается подстановкой):

три одномерные задачи, их решения:

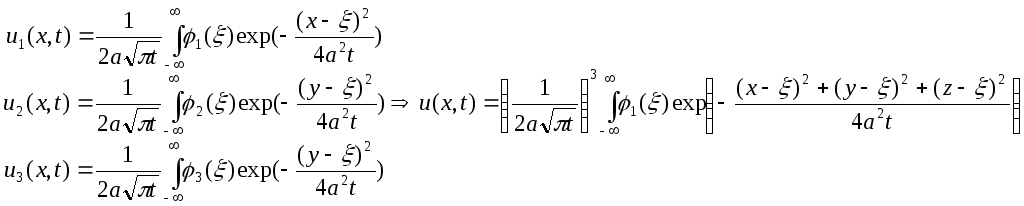
функция Грина в трёхмерном пространстве: .

начальное условие соответствующие трёхмерной задачи.:

11.Смешанная краевая задача и задача Коши с уравнением .

		Разбиваем задачу на три, каждая из которых вызывает одну причину: начальное отклонение, (), внешние силы, т.е.
1) Учитываем граничные условия: подбираем u1 таким, что бы оно удовлетворяло граничным условиям: В силу линейности оставшиеся два решения удовлетворяют однородным граничным условиям	2) Учитываем начальные условия, не учитываем правую часть: ищем u2 такое, которое удовлетворяет однородному уравнению и однородным граничным условиям, а также получим новые начальные условия: Мы получили однородную задачу для u2 с неоднородными начальными условиями. Её решение в вопросе 8.		3) Учитываем начальные условия, не учитываем правую часть: ищем u3 такое, что бы оно удовлетворяло неоднородному уравнению, и получаем для него нулевые условия:. Мы разделили задачу таким образом, что сумм этих трёх частей удовлетворяет исходным уравнению и условиям.

Рассмотрим все эти задачи по отдельности:

ВОПРОС12а! 2)		з. Ш.-Л. Задача на собств. знач.: Если решение есть оно должно удовлетворять решению и начальным условиям. Запишем теорему Стеклова: :
- коэффициенты разложения по ортогональному базису: получили уравнение уравнение, которому удовлетворяет Сn. Его общее решение: , подставим: , коэффициенты находим из начальных условий. - разложили в ряд по собственным функциям задачи Ш.-Л.
3)	Воспользуемся т. с. зн. , если решение существует, то - разложили решение в ряд по собственным значениям, коэффициенты разложения ( - самосопряженный оператор):
удовлетворяет уравнению: неоднородное линейное дифференциальное уравнение второго порядка, начальные условия получаем исходя из начальных условий задачи. , тогда решение этого уравнения :

b. Постоянные коэффициенты на отрезке.

Рассмотрим смешанная краевая задача с однородным уравнением с постоянными коэффициентами на отрезке.

можно решить методом разделения переменных, или в общем виде:

(см. предыдущий билет).

В нашем случае: есть решение: коэффициенты находим их начальных условий.

13.Теорема о max и min

Рассмотрим уравнение:

Всякое решение этого уравнения , непрерывное в области , принимает наибольшее и наименьшее значения или на нижней границе области при , или на боковых границах

Доказательство: если =const, то утверждение очевидно, пусть . Докажем теорему для наибольшего значения:

– наибольшее значение на границах

– наибольшее значение в области

Надо доказать, что =. предположим что >. Введём вспомогательную функцию:

, она достигает наибольшего значения в области в некоторой точке , очевидно, что , т.к. в . Точка не может лежать ни на одной из граней, т.к.: , а

таким образом, точкапринадлежит области , поэтому в ней функция должна удовлетворять (1), но

получили противоречие, значит =ч.т.д.