2.2. Решение задачи Табличная модель
Обычно план назначений составляется в виде таблицы.
Перед менеджером фирмы «Стар» стоит задача распределения четырех работников по вакантным должностям по условиям результатов контрольных испытаний. Производительность труда по определенным видам работ, показанная каждым из работников, приведена в таблице.
Пример приведен в табл. 2.1.
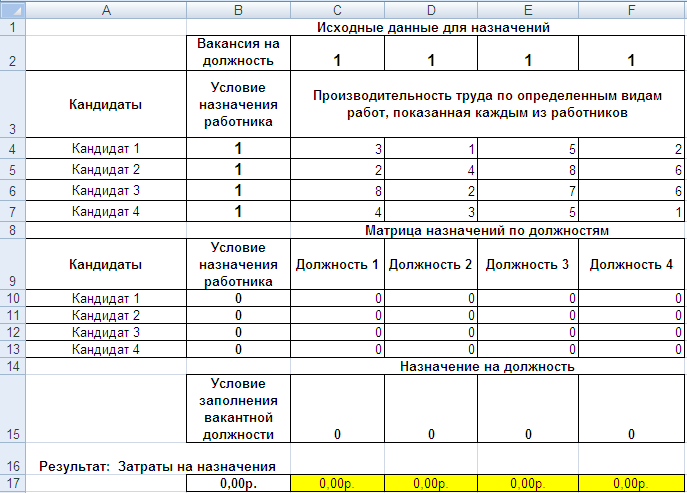
В верхней строке электронной таблицы Excel даны имена колонок А, В, С...
В первой колонке — номера строк.
В колонке А — приведены условные кандидаты на занимаемые должности.
В строке 9 — приведены условные названия вакантных должностей.
Искомые показатели выделены желтым цветом.
В17 – общие плановые затраты на назначения.
С4:F7 – производительность труда кандидатов, выявленная при проведении контрольных испытаний по каждой должности.
Общие плановые затраты на назначения в ячейке В17 надо максимизировать.
Искомая плановая матрица назначений каждого кандидата на вакантную должность расположена в диапазоне C10:F17.
В диапазоне B10:B13 определяется план назначения на должность, как суммы по строкам.
В строке 15 фиксируется результат назначений.
Плановик наблюдает, чтобы соблюдался принцип Одна должность – один кандидат.
В диапазон В4:В7 фиксируется основной принцип данной задачи, на одну должность должен быть назначен один кандидат.
В матрицу С4:F7 надо ввести производительность труда кандидата при назначении его на конкретную должность.
В строку 2 фиксируем потребности в заполнении вакантной должности (1).
В строке 15 вычисляются стоимость назначения кандидатов на выбранную должность и общие затраты при назначении.
Математическая модель
Введем обозначения:
m — количество вакантных должностей;
i — номер строки, работника, 1 ..n;
j — номер столбца, должности, 1 ..m;
X — искомое плановое назначение i-го работника на j-ую должность;
В общем виде наша модель экономико-математической постановки задачи будет выглядеть следующим образом:
суммарная производительность труда работников (целевая функция).
P= max
При следующих ограничениях:
=1
=1
Формулы табличной модели
После составления плановой таблицы необходимо связать показатели формулами для вычислений. Представление формул и чисел исходных данных дано в табл. 2.2.
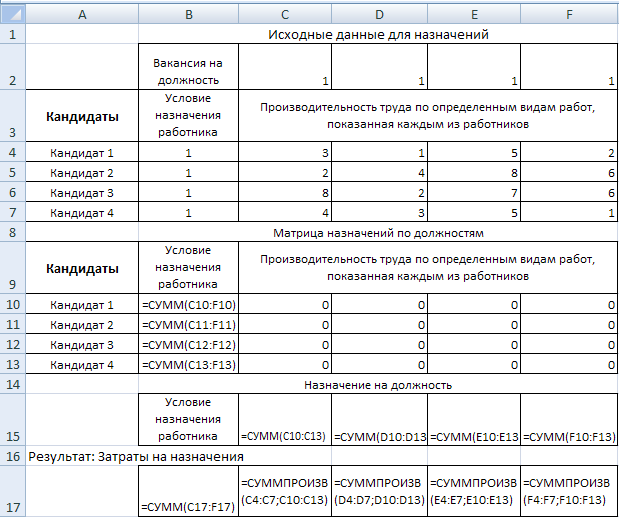
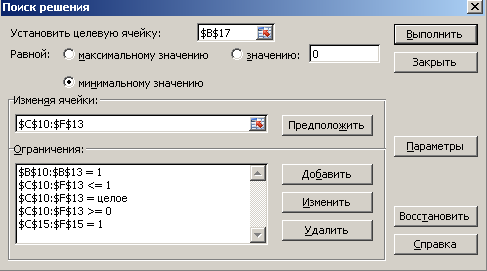
Рис. 2.2. Диалоговое окно Поиск решения с координатно-математической моделью задачи назначения
Для конкретной задачи вариант назначений с наименьшими затратами равен
10 Ден. Единиц.
Из полученной таблицы можно сделать следующий вывод: минимум затрат на назначение, равный 10 ден. единиц, будет обеспечен при следующем варианте назначений:
Кандидат 1 назначен на третью должность с производительностью 5 у. единиц.
Кандидат 2 назначен на первую должность с производительностью 2 у. единиц.
Кандидат 3 назначен на вторую должность с производительностью 2 у. единиц.
Кандидат 4 назначен на четвертую должность с производительностью 1 у. единиц.
Контрольные вопросы для защиты работы
1. Почему актуальна проблема оптимального варианта назначений?
2. Сформулировать цель работы.
3. Перечислить объекты проблемной системы.
4. Пояснить структуру плановой таблицы.
5. Перечислить исходные данные, переменные и результирующие показатели модели.