Анализ результатов и решения менеджера
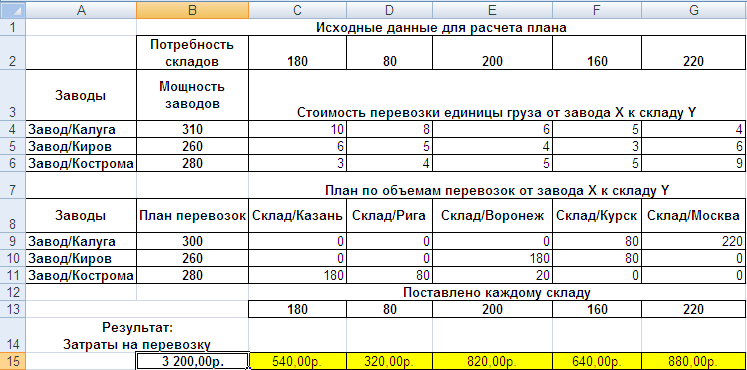
Табл. 2.2. Результат решения задач с использованием программы Поиск решения
В табл. 2.2. дано оптимальное решение, найденное программой Поиск решения.
Можно утверждать, что получена матрица перевозок, содержащая оптимальный объем поставок грузов от производителя потребителям, дающий минимум затрат на доставку.
Для конкретной задачи план перевозок с наименьшими затратами равен 3 200 руб.
Из полученной таблицы можно сделать следующий вывод: минимум затрат на доставку, равный 3 200 руб., будет обеспечен при следующем плане поставок:
от Завода/Калуга Складу/Курска в объеме 80 единиц и Складу/Москва в объеме 220 единиц (условных).
от Завода/Киров Складу/Курска в объеме 80 единиц и Складу/Воронеж в объеме 180 единиц (условных).
от Завода/Кострома Складу/Казань в объеме 180 единиц, Складу/Рига в объеме 80 единиц (условных) и Складу/Воронеж в объеме 20 единиц (условных).
Анализ Мощности заводов и Плана перевозок позволил сделать вывод, что наша задача не сбалансированная, т.к. при производстве 310 условных единиц продукции, были востребованы только 300 у. единиц.
Эта дает нам возможность принять одно из двух управленческих решений:
Снизить производство на Заводе/Калуга продукции на 10 у. единиц.
Найти нового потребителя на невостребованную продукцию.
Оформление отчета
Отчет должен содержать:
1.Определение проблемы.
2.Плановую таблицу с результатом оптимального плана.
З. Анализ оптимального плана и решения менеджера.
4.Формулы модели для оптимизации транспортной задачи.
Контрольные вопросы для защиты работы
1. Почему актуальна проблема оптимального плана перевозок?
2. Сформулировать цель работы.
3. Перечислить объекты проблемной системы.
4. Пояснить структуру плановой таблицы.
5. Перечислить исходные данные, переменные и результирующие показатели модели.
6. Дать краткую технологию решения транспортной задачи в программе Excel Поиск решения
2. Целочисленное программирование, задача о назначениях
2.1. Постановка задачи
В общем случае постановка задачи о назначениях заключается в том, что необходимо распределить необходимое количество должностей между определенным количеством кандидатов. При этом данные задачи являются логическими, т.к искомые переменные принимают значения – нуль или единица. Оптимальный подбор назначений может быть достигнут за счет максимизации или минимизации определенной меры эффективности назначения: прибыли или стоимости
Цели решения данной задачи
Научиться составлять наилучший (оптимальный) план назначения работников на имеющиеся вакантные должности, с учетом имеющихся показателей.
Освоить методику и технологию оптимизации планов в табличном процессоре Excel с помощью программы Поиск решения (Solver).
Выделение проблемной системы
В проблемную систему включаем следующие объекты и показатели: перечень кандидатов на работу и вакансий, а так же производительность труда в зависимости от опыта работы, квалификации, индивидуальных особенностей.
Постановка задачи
Рассмотрим нашу задачу сначала для меры эффективности – прибыли, следовательно, основным условием поставленной задачи является максимизация производительности труда в коллективе при условии, что каждый работник может быть назначен только на одну работу.
Далее рассмотрим нашу задачу для меры эффективности - стоимость в этом случае основным условием поставленной задачи будет является минимизация затрат на оплату труда в коллективе при условии, что каждый работник может быть назначен только на одну работу.