МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ
Кафедра ЭФ-4 «Бухучет, финансы и аудит»
УТВЕРЖДАЮ
Заведующий кафедрой ЭФ-4
_______(Бондарчук Н.В.)
«__» июня 2007г.
Для студентов 2го курса экономического факультета
Специальностей 08.0105 и 08.0109
К.э.н., доцент, Нечаева Т.В. и ст. преподаватель Ложкомоева Е.Н.
(ученая степень, ученое звание, фамилия и инициалы автора)
ЛЕКЦИЯ № 9
по дисциплине 5483 (Эконометрика)
ТЕМА «Моделирование сезонных и циклических колебаний временного ряда»
Обсуждена на заседании кафедры
(предметно-методической секции)
«___»___________2007г.
Протокол № __
МГУПИ – 2007г.
Тема лекции: «Моделирование сезонных и циклических колебаний временного ряда»
Учебные и воспитательные цели:
Формирование у студентов представления о важности исследования периодических колебаний экономических процессов
Изучение способа проверки наличия циклических колебаний на основе анализа коэффициентов автокорреляции и построения коррелограммы
Изучение разных подходов к моделированию циклических колебаний
Время: 2 часа (90 мин.).
Литература (основная):
«Эконометрика», под редакцией Елисеевой И.И., М., «Финансы и статистика», 2005г
Елисеева И.И., Курышева С.В., Гордеенко Н.М., Бабаева И.В., Костеева Т.В., Михайлов Б.А., «Практикум по эконометрике», Изд-во «Финансы и статистика», Москва, 2004.
Литература (дополнительная):
Тихомиров Н.П., Дорохина Е.Ю., «Учебно-методическое пособие по дисциплине «Эконометрика», Изд-во РЭА., Москва, 2004.
Кремер Н.Ш., Путко Б.А., «Эконометрика: Учебник для вузов», ЮНИТИ-ДАНА, Москва, 2004.
Доугерти К., «Введение в эконометрику», Инфра-М, Москва, 2004.
Учебно-материальное обеспечение:
Наглядные пособия: раздаточный материал в виде плакатов
Технические средства обучения: электронный конспект лекций
План лекции:
Введение – до 5 мин.
Основная часть (учебные вопросы) – до 80 мин.
1-й учебный вопрос: Анализ автокорреляции во временных рядах и определение длины цикла - 30 мин.
2-й учебный вопрос: Выявление сезонной компоненты – 10 мин.
3-й учебный вопрос: Моделирование циклических колебаний с помощью рядов Фурье – 40 мин.
Заключение – до 5 мин.
ТЕКСТ ЛЕКЦИИ «МОДЕЛИРОВАНИЕ СЕЗОННЫХ И ЦИКЛИЧЕСКИХ КОЛЕБАНИЙ ВРЕМЕННЫХ РЯДОВ»
Введение.
На предыдущей лекции мы ознакомились с анализом структуры временных рядов и способами проверки гипотезы о наличии тренда с помощью разных статистических критериев.
Сегодня мы рассмотрим способ выявления периодических (сезонных или циклических) колебаний и определения длины цикла (периода колебаний) на основе анализа автокорреляции временного ряда.
Помимо тренда (основной тенденции) в любом временном ряду может присутствовать (либо отсутствовать) циклическая компонента. Для выявления наличия циклической компоненты проводится анализ автокорреляции временного ряды и рассчитывают коэффициенты автокорреляции разного порядка. Изучая способы проверки предпосылок метода наименьших квадратов, мы уже упоминали о проверке наличия или отсутствия автокорреляции остатков с помощью критерия Дарбина-Уотсона. Этот критерий основан на оценке коэффициента автокорреляции только первого порядка. Для анализа автокорреляции временных рядов рассчитывают коэффициенты автокорреляции более высокого порядка и на их основе определяют наличие циклических колебаний и длину цикла. На данной лекции мы рассмотрим расчет этих коэффициентов, а также способы, которые обычно используют для моделирования сезонных и циклических колебаний.
1Й учебный вопрос. Анализ автокорреляции временного ряда и определение длины цикла.
Автокорреляция – корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные данные).
При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.
Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.
Формула для расчета коэффициента автокорреляции первого порядка имеет вид:
(9.1)
где
Эту величину
называют коэффициентом автокорреляции
уровней ряда первого порядка, так как
он измеряет зависимость между соседними
уровнями ряда:
и
.
Аналогично можно
определить коэффициенты автокорреляции
второго и более высоких порядков. Так,
коэффициент автокорреляции второго
порядка характеризует тесноту связи
между уровнями
и
и определяется по формуле:
(9.2)
где
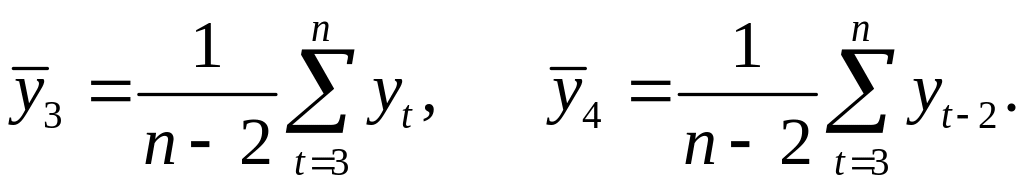
Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом.
С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Считается целесообразным для обеспечения статистической достоверности коэффициентов автокорреляции использовать правило – максимальный лаг должен быть не больше n/4.
Отметим два важных свойства коэффициента автокорреляции. Во-первых, он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровня ряда. Поэтому по величине коэффициента автокорреляции можно судить только о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту) коэффициент автокорреляции уровней исходного ряда может приближаться к нулю.
Во-вторых, по знаку коэффициента автокорреляции нельзя сделать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержит положительную автокорреляцию уровней, однако они при этом могут иметь убывающую тенденцию.
Последовательность коэффициентов разных порядков называют автокорреляционной функцией временного ряда.
График ее зависимости от величины лага (порядка коэффициента автокорреляции) называется коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором связь между текущим и предыдущим уровнями ряда наиболее тесная, т.е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру временного ряда. Если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка τ, то ряд содержит циклические колебания с периодом в τ моментов времени, то есть длина цикла равна τ. Если ни один из коэффициентов автокорреляции не является значимым (все они близки к нулю), то либо ряд вообще не содержит тенденцию и циклические колебания (а только случайные колебания), либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужен дополнительный анализ. Рассмотрим пример расчета коэффициентов автокорреляции для двух различных временных рядов.
Первый ряд характеризует расходы на конечное потребление за 8 лет, а второй – потребление электроэнергии жителями региона за 16 кварталов (т.е. за четыре года).
Исходные данные и рассчитанные коэффициенты автокорреляции для первого ряда приведены в таблице 9.1.
Соответственно исходные данные для анализа автокорреляции второго ряда приведены в таблице 9.2.
Таблица 9.1
Расчет коэффициентов автокорреляции для временного ряда расходов на конечное потребление
-
t
yt
yt-1
yt-2
yt-3
yt-4
i (лаг)
ri
1
7
-
-
-
-
1
0,9765
2
8
7
-
-
2
0,9728
3
8
8
7
-
-
3
0,9623
4
10
8
8
7
-
4
0,9259
5
11
10
8
8
7
-
-
6
12
11
10
8
8
-
-
7
14
12
11
10
8
-
-
8
16
14
12
11
10
-
-
Результаты расчета коэффициентов автокорреляции в таблице 9.1 показывают, что практически все коэффициенты автокорреляции близки к единице. Это означает, что в ряду имеется ярко выраженная линейная тенденция (тренд), а периодическая (сезонная или циклическая) компонента отсутствует.
Таблица 9.2.