Вспомогательная таблица для расчета теоретических частот нормального распределения

Крепость нити, г		Число проб	Середина интервала			φ(t)	154,3 φ(t)	f
1		2	3	4	5	6	7	8
120	130	1	125	-36	-2,81	0,008	1,2	1
130	140	8	135	-26	-2,04	0,050	7,7	8
140	150	27	145	-16	-1,27	0,179	27,6	28
150	160	58	155	-6	-0,49	0,353	54,5	55
160	170	56	165	4	0,28	0,384	59,2	59
170	180	34	175	14	1,05	0,230	35,5	35
180	190	14	185	24	1,82	0,076	11,7	12
190	200	2	195	34	2,59	0,014	2,1	2
		200					200	200

Для нахождения теоретических частот используем формулу (7.2):

Эта формула может быть записана в упрощенной форме, как:

где - нормированные отклонения значений признака от их средней величины.

Не приводя здесь вспомогательных расчетов, укажем сразу, что

= 161,4

= 13.

Далее выполняем следующие действия:

1. Находим отклонения значений признака от их средней (в графе 4 таблицы 7.1);

2. делим каждое отклонение на , т.е. находим нормированные отклонения (в графе 5 таблицы 7.1);

3. в графе 6 находим либо по специальной таблице, либо рассчитывая эту функцию непосредственно по формуле (7.1). Такие расчеты могут быть выполнены в программе Excel.

4. Затем определяем величину постоянного множителя для расчета теоретических частот по формуле (7.2), то есть величину:

5. Наконец, в графе 7 рассчитываем значения теоретических частот по формуле (7.2) и затем (в графе 8) округляем эти значения до целых.

Как видно из таблицы 7.1, теоретические значения очень близки к фактическим, хотя кое-где заметны расхождения.

Чтобы оценить, насколько эти отклонения теоретических частот от фактических являются существенными, или наоборот, чисто случайными, воспользуемся критериями согласия.

Вначале рассчитаем значение критерия Пирсона, воспользовавшись вспомогательной таблицей 7.2.

Таблица 7.2

Вспомогательная таблица для расчета критерия Пирсона

m	f	m-f	(m-f)2	(m-f)2/f
1	1	0	0	0,00
8	8	0	0	0,00
27	28	-1	1	0,04
58	55	3	9	0,16
56	59	-3	9	0,15
34	35	-1	1	0,03
14	12	2	4	0,33
2	2	0	0	0,00
200	200			χ2 = 0,71

Критерий Пирсона, как было отмечено ранее, рассчитывается по формуле (7.3)

В таблице 7.2 выполнен расчет всех необходимых составных элементов данной формулы и найдено окончательное значение критерия χ² = 0,71.

В данном примере всего 8 групп (классов) статистических единиц, у которых значения признака располагаются в соответствующем интервале. Поэтому число степеней свободы k для определения табличного значения критерия Пирсона может быть найдено как: k =8-3=5.

Примем наиболее часто используемый уровень значимости α = 0,05 и найдем табличное значение критерия Пирсона.

Легко убедиться, что χ² _табл = 11,07. Так как рассчитанное в примере фактическое значение критерия 0,71 значительно меньше табличного, то отсюда можно сделать вывод о том, что расхождения между теоретическими и фактическими частотами являются случайными, и следовательно принять гипотезу о близости фактического распределения к нормальному закону.

Применим теперь критерий Романовского, воспользовавшись формулой (7.4):

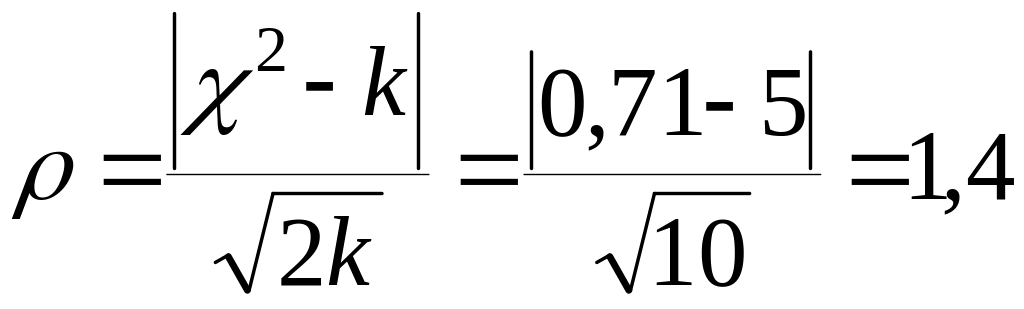
Так как 1,4 < 3, то можно считать расхождения между теоретическими и фактическими частотами случайными. Критерий Романовского также показывает, что можно принять гипотезу о близости фактического распределения к нормальному.

Теперь проверим гипотезу о нормальном распределении с помощью критерия Колмогорова, воспользовавшись формулой (7.6):

λ =

Для этого рассчитаем накопленные частоты фактического и теоретического распределений и найдем величину максимального расхождения между ними.

Вспомогательные расчеты приведены в таблице 7.3.

В таблице 7.3. S(m)- обозначает накопленные частоты фактического распределения, а S(f) – накопленные частоты теоретического распределения.

Легко убедиться, что максимальный разрыв между ними D =2.

Таблица 7.3

Вспомогательная таблица для расчета критерия Колмогорова

m	f	Накопленные частоты		|Sm-Sf|
		S (m)	S(f)
1	1	1	1	0
8	8	9	9	0
27	28	36	37	1
58	55	94	92	2
56	59	150	151	1
34	35	184	186	2
14	12	198	198	0
2	2	200	200	0

Отсюда находим λ =

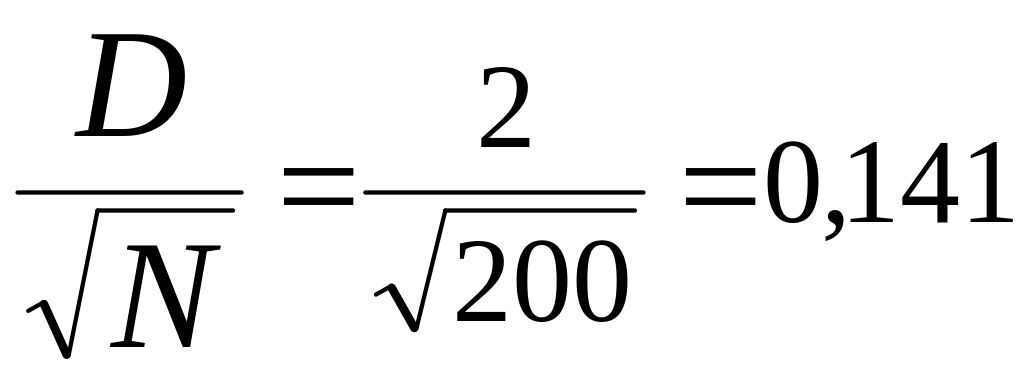
По специальной статистической таблице, разработанной для данного критерия, находим, что при λ=0,141 вероятность P(λ) = 1,000, то есть с очень большой вероятностью можно предположить, что расхождения между фактическими и теоретическими частотами носят случайный характер.

Таким образом, в данном случае все три критерия согласия дали один и тот же результат, то есть показали, что гипотеза о нормальном характере распределения может быть принята для данного распределения с вероятностью 95%.

Теперь рассмотрим применение этих критериев к проверке гипотезы о нормальном распределении ряда остатков в уравнении нелинейной регрессии.