МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ

Кафедра ЭФ-4 «Бухучет, финансы и аудит»

УТВЕРЖДАЮ

Заведующий кафедрой ЭФ-4

_______(Бондарчук Н.В.)

«__» июня 2007г.

Для студентов 2го курса экономического факультета

Специальностей 08.0105 и 08.0109

Канд. экон. наук, доцент, Нечаева Т.В., ст. преподаватель Ложкомоева Е.Н.

(ученая степень, ученое звание, фамилия и инициалы авторов)

ЛЕКЦИЯ № 7

по дисциплине 5483 (Эконометрика)

ТЕМА «Проверка гипотезы о нормальном распределении случайной величины»

Обсуждена на заседании кафедры

(предметно-методической секции)

«___»___________2007г.

Протокол № __

МГУПИ – 2007г.

Тема лекции: «Проверка гипотезы о нормальном распределении случайной величины»

Учебные и воспитательные цели:

1. Ознакомление студентов с особенностями закона нормального распределения случайной величины

2. Изучение критерия Пирсона для проверки гипотезы о нормальном распределении

3. Изучение критерия Колмогорова для проверки гипотезы о нормальном распределении

4. Применение изученных критериев для проверки гипотезы о нормальном распределении ряда остатков

Время: 2 часа (90 мин.).

Литература (основная):

1. «Эконометрика», под редакцией Елисеевой И.И., М., «Финансы и статистика», 2005г

2. Елисеева И.И., Курышева С.В., Гордеенко Н.М., Бабаева И.В., Костеева Т.В., Михайлов Б.А., «Практикум по эконометрике», Изд-во «Финансы и статистика», Москва, 2004.

Литература (дополнительная):

3. Тихомиров Н.П., Дорохина Е.Ю., «Учебно-методическое пособие по дисциплине «Эконометрика», Изд-во РЭА., Москва, 2004.

4. Кремер Н.Ш., Путко Б.А., «Эконометрика: Учебник для вузов», ЮНИТИ-ДАНА, Москва, 2004.

5. Доугерти К., «Введение в эконометрику», Инфра-М, Москва, 2004.

Учебно-материальное обеспечение:

1. Наглядные пособия: раздаточный материал в виде плакатов

2. Технические средства обучения: электронный конспект лекций

План лекции:

Введение – до 5 мин.

Основная часть (учебные вопросы) – до 80 мин.

1-й учебный вопрос: Особенности закона нормального распределения случайной величины - 15 мин.

2-й учебный вопрос: Статистические критерии согласия Пирсона и Романовского – 20 мин.

3-й учебный вопрос: Статистический критерий согласия Колмогорова – 25 мин.

4й учебный вопрос: Проверка гипотезы о нормальном распределении ряда остатков- 20 мин.

Заключение – до 5 мин.

ТЕКСТ ЛЕКЦИИ

Введение.

На предыдущей лекции мы рассмотрели проблемы построения нелинейных уравнений регрессии и возможность нарушения основных предпосылок МНК. Затем мы рассмотрели методы проверки этих предпосылок на конкретном примере и остановились на том, что в случае необходимости проверки гипотезы о нормальном законе распределения ряда остатков расчет показателей асимметрии и эксцесса может не дать точного ответа на вопрос о характере распределения, и что в этом случае необходимо пользоваться более мощными статистическими критериями, к которым, в частности, относятся критерий Пирсона и критерий Колмогорова.

На данной лекции мы более подробно рассмотрим суть этих критериев и их практическое применение для проверки гипотезы о нормлаьном распределении ряда остатков.

1й учебный вопрос. Особенности закона нормального распределения случайной величины.

В эконометрике (как и в статистике) часто возникает необходимость выравнивания (сглаживания) вариационных рядов. Под выравниванием ряда понимается замена распределения фактических частот значений признака близким к нему по характеру теоретическим. Из многих кривых распределения, по которым может выравниваться вариационный ряд, наиболее часто на практике используется кривая нормального распределения. Как известно, большинство явлений в природе и обществе распределено по нормальному закону. График нормального распределения случайной величины (признака) x имеет форму колоколообразной кривой, симметричной относительно , концы которой асимптотически приближаются к оси абсцисс. Она имеет точки перегиба, абсциссы которых находятся на расстоянии σ от центра симметрии.

График такой кривой соответствует графическому изображению функции:

(7.1)

где - ордината кривой нормального распределения;

- нормированные отклонения значений признака x от их средней величины.

Этот график имеет примерно такой вид, как кривая, изображенная на рис.7.1

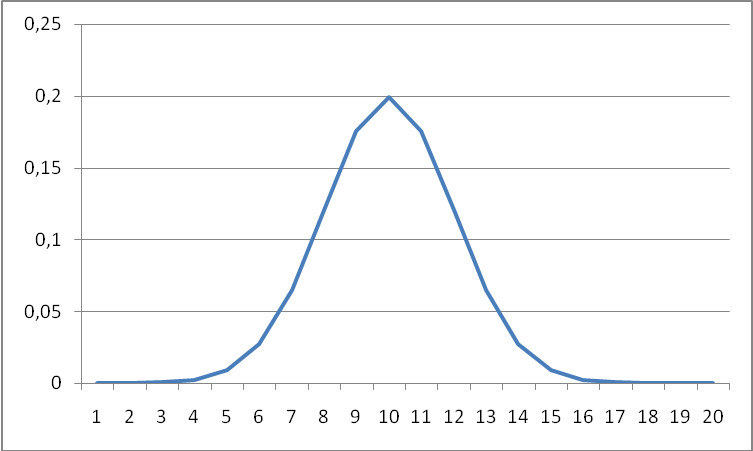
Рис. 7.1. Кривая нормального распределения

При выравнивании вариационного ряда по кривой нормального распределения теоретические частоты ряда определяются по формуле:

(7.2)

В этой формуле:

- сумма всех частот вариационного ряда;

h – величина интервала;

σ – среднее квадратическое отклонение значений признака от их средней величины;

- нормированные отклонения значений признака x от их средней величины.

Величина находится по специальной таблице как функция φ (t).

Как видно из формулы (7.1) основными параметрами кривой нормального распределения являются и σ. По этим характеристикам ее легко построить для любого ряда распределения.

Однако после выравнивания ряда распределения по кривой нормального распределения (т.е. нахождения теоретических частот) возникает необходимость проверить, являются ли случайными расхождения между фактическими и теоретическими значениями частот. Это позволит проверить правильность выдвинутой при выравнивании ряда гипотезы о том, что данный ряд значений признака действительно подчиняется нормальному закону распределения.

Для оценки близости теоретических и фактических частот ряда распределения обычно используют один из статистических критериев: критерий Пирсона χ² (или критерий «хи-квадрат»), критерий Романовского, критерий Колмогорова λ (или - «лямбда-критерий»).

Эти статистические критерии в статистике и эконометрике обычно называют критериями согласия. Далее мы рассмотрим каждый из них более подробно.