МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ

Кафедра ЭФ-4 «Бухучет, финансы и аудит»

УТВЕРЖДАЮ

Заведующий кафедрой ЭФ-4

_______(Бондарчук Н.В.)

«__» июня 2007г.

Для студентов 2го курса экономического факультета

Специальностей 08.0105 и 08.0109

Канд. экон. наук, доцент, Нечаева Т.В., ст. преподаватель Ложкомоева Е.Н.

(ученая степень, ученое звание, фамилия и инициалы авторов)

ЛЕКЦИЯ № 2

по дисциплине 5483 (Эконометрика)

ТЕМА «Сущность метода наименьших квадратов (МНК) и его предпосылки: построение уравнений парной линейной регрессии»

Обсуждена на заседании кафедры

(предметно-методической секции)

«___»___________2007г.

Протокол № __

МГУПИ – 2007г.

Тема лекции: «Cущность МНК и его предпосылки: построение уравнений парной линейной регрессии»

Учебные и воспитательные цели:

1. Ознакомление студентов с математическими основами метода наименьших квадратов

2. Изучение сущности метода наименьших квадратов (МНК)

3. Усвоение способа построения уравнений парной линейной регрессии с помощью МНК

Время: 2 часа (90 мин.).

Литература (основная):

1. «Эконометрика», под редакцией Елисеевой И.И., М., «Финансы и статистика», 2005г

2. Елисеева И.И., Курышева С.В., Гордеенко Н.М., Бабаева И.В., Костеева Т.В., Михайлов Б.А., «Практикум по эконометрике», Изд-во «Финансы и статистика», Москва, 2004.

Литература (дополнительная):

3. Тихомиров Н.П., Дорохина Е.Ю., «Учебно-методическое пособие по дисциплине «Эконометрика», Изд-во РЭА., Москва, 2004.

4. Кремер Н.Ш., Путко Б.А., «Эконометрика: Учебник для вузов», ЮНИТИ-ДАНА, Москва, 2004.

5. Доугерти К., «Введение в эконометрику», Инфра-М, Москва, 2004.

Учебно-материальное обеспечение:

1. Наглядные пособия: раздаточный материал в виде плакатов

2. Технические средства обучения: электронный конспект лекций

План лекции:

Введение – до 5 мин.

Основная часть (учебные вопросы) – до 80 мин.

1-й учебный вопрос: Математические основы МНК - 25 мин.

2-й учебный вопрос: Сущность МНК и его предпосылки – 25 мин.

3-й учебный вопрос: Построение уравнения парной линейной регрессии – 20 мин.

4й учебный вопрос: Интерпретация параметров уравнения парной регрессии – 10 мин

Заключение – до 5 мин.

ТЕКСТ ЛЕКЦИИ

Введение.

Сегодня мы изучим основной метод, который используется для построения эконометрических моделей – метод наименьших квадратов. Суть данного метода кратко рассматривалась в курсе теории статистики.

Но ранее мы его рассматривали очень упрощенно, в основном, как способ построения уравнений тренда и простейших уравнений регрессии. Сегодня мы рассмотрим математические основания этого метода, теоретические предпосылки, которые положены в его основу, и его использование на примере построения уравнений парной линейной регрессии. В дальнейшем мы рассмотрим более детально особенности уравнений множественной линейной регрессии.

1Й учебный вопрос. Математические основы метода наименьших квадратов.

Ранее (в курсе теории статистики) мы уже отмечали, что любое уравнение регрессии представляет собой уравнение некоторой математической функции, приближенно описывающее статистическую зависимость между показателями. Постановку задачи выбора наиболее подходящей функции рассмотрим на примере уравнения парной регрессии.

Пусть у нас есть набор значений двух переменных: x_t, y_t, t=1,2,..., n. Предположим, что задачей является подобрать функцию y=f(x) из параметрического семейства функций f(x, α), наилучшим образом описывающую зависимость y от x. Поиск функции данного типа означает практически, что нужно выбрать "наилучшее" значение параметра α.

В качестве меры отклонения функции f (x, α) от набора наблюдений можно взять:

- сумму квадратов отклонений, т.е.

;

- сумму модулей отклонений, т.е.

;

- или в общем случае

,

где g - "мера", с которой отклонение входит в функцию F.

Достоинства и недостатки перечисленных функционалов:

1) Сумма квадратов отклонений

плюсы:

- легкость вычислительной процедуры;

- хорошие статистические свойства, простота математических выводов, тщательная проверка различных статистических гипотез.

минусы:

- чувствительность к «выбросам» (неожиданным, резким изменениям в ряду исходных статистических данных, когда например, соседние значения отличаются на порядок).

2) Сумма модулей отклонений

плюсы:

- нечувствительность к выбросам.

минусы:

- сложность вычислительной процедуры;

- возможность больших отклонений между фактическими и проектными функциями;

- неоднозначность значений параметров и т.д.

Исходя из этих преимуществ и недостатков, обычно в качестве меры близости выбирают сумму квадратов и выбирают такую функцию y=f(x), у которой эта сумма квадратов достигает минимума.

Для того, чтобы лучше понять сущность метода наименьших квадратов, необходимо вначале вспомнить математические основы определения экстремума функции нескольких переменных.

В первую очередь, введем некоторые определения:

Определение 1. Функция Z = ƒ (x, y) имеет максимум в точке М₀ (х₀, у₀), если значение функции в этой точке больше значений ее в точках, достаточно близких к точке М₀ (х₀, у₀), т.е.

ƒ (х₀, у₀) > ƒ (х₀ + Δх, у₀ + Δу).

Это означает, что полное приращение функции Z = ƒ (х, у), вызванное переходом от точки (х₀, у₀) к соседней точке, будет величиной отрицательной:

ΔZ = ƒ (х₀ + Δх, у₀ + Δу) - ƒ (х₀, у₀) < 0. (2.1)

Определение 2. Функция Z = ƒ (x, y) имеет минимум в точке М₀ (х₀, у₀), если значение функции в этой точке меньше значений ее в точках, достаточно близких к точке М₀ (х₀, у₀), т.е.

ƒ (х₀, у₀) < ƒ (х₀ + Δх, у₀ + Δу).

Это означает, что полное приращение функции Z = ƒ (х, у), будет величиной положительной:

ΔZ = ƒ (х₀ + Δх, у₀ + Δу) - ƒ (х₀, у₀) > 0. (2.2)

Допустим, что функция Z = ƒ (х, у) имеет в точке М₀ (х₀, у₀) максимум или минимум (экстремум).Тогда для функции должно выполняться одно из неравенств (3.1) или (3.2) при любых, достаточно малых Δх, Δу.

Предположим, что Δу = 0; тогда функция Z = ƒ (х, у) сделается функцией только одной переменной х. Эта функция по условию имеет экстремум.

Таким образом, условия обращения в нуль частных производных функции или несуществование хотя бы одной из них являются необходимыми условиями, но недостаточными условиями экстремума функции.

Имеем систему:

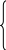
. (2.4)

Условия (2.4) являются необходимыми для существования экстремума функции. Но может случиться, что эти условия в некоторых обстоятельствах невыполнимы.

Достаточные условия существования экстремума функции нескольких переменных имеют более сложный вид.

Пусть в точке М₀ (х₀, у₀) частные производные обращаются в нуль, т.е.

, .

Подсчитаем значения частных производных второго порядка функции

Z = ƒ (х, у) в этой точке и обозначим их соответственно буквами: А, В, С:

тогда:

1. Если АС - В² > 0, то функция Z = ƒ (х, у) имеет в точке М₀ (х₀, у₀) экстремум, а именно:

при А < 0 максимум,

при А > 0 минимум.

2. Если АС - В² < 0, то функция Z = ƒ (х, у) не имеет в точке М₀ (х₀, у₀) экстремума.

3. Если АС - В² = 0, то вопрос о существовании экстремума функции в точке М₀ (х₀, у₀) остается открытым и требуются дополнительные исследования.

Метод наименьших квадратов является одним из важных применений теории экстремума функции нескольких переменных.

Предположим, что в результате некоторого опыта или наблюдения установлена зависимость между переменными величинами х и у, выражаемая в виде таблицы:

х	х1	х2	…	хn
у	у1	у2	…	уn

Пусть требуется перейти от табличного метода задания функции к аналитическому (т.е. выраженному в виде формулы), причем, если это нельзя сделать точно, постараемся получить аналитическую связь приближенно.

Теперь обратимся к графическому изображению данной системы. Рассматривая значения х и у как координаты точек в прямоугольной системе координат, наносим эти точки на график. Пусть, например, построенные точки расположены достаточно близко к некоторой прямой. Поэтому можно приблизительно считать, что между х и у существует линейная зависимость, выражаемая формулой,

у = ах + b.

Поставим задачу аналитического определения неизвестных коэффициентов а и b.

В основе аналитического метода определения а и b лежит метод наименьших квадратов. Точки, полученные на основании опытных данных, вообще говоря, не лежат на искомой прямой. Если бы некоторая точка (х_i, у_i) лежала на прямой, то ее координаты удовлетворяли бы уравнению прямой, т.е. имело бы место равенство:

у_i = ax_i + b или ax_i + b - y_i = 0

Однако в общем случае подстановка координат точки в уравнение прямой дала бы:

ax_i + b - y_i = ε_i,

где ε_i ─ какая то малая величина.