16.Определение циклического кода принцип построения.
Циклический код — линейный код, обладающий свойством цикличности, то есть каждая циклическая перестановка кодового слова также является кодовым словом. Используется для преобразования информации для защиты её от ошибок (см. Обнаружение и исправление ошибок).
Несистематическое
При несистематическом кодировании кодовое слово получается в виде произведения информационного полинома на порождающий
.
Оно может быть реализовано при помощи перемножителей полиномов.
Систематическое
При
систематическом кодировании кодовое
слово формируется в виде информационного
подблока и проверочного
Пусть информационное слово образует старшие степени кодового слова, тогда
Тогда
из условия
,
следует
Это уравнение и задает правило систематического кодирования. Оно может быть реализовано при помощи многотактных линейных фильтров(МЛФ)
Пример
Двоичный (7,4,3) код
В
качестве делителя
выберем
порождающий полином третьей степени
,
тогда полученный код будет иметь длину
,
число проверочных символов (степень
порождающего полинома)
,
число информационных символов
,
минимальное расстояние
.
Порождающая матрица кода:
,
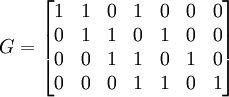где
первая строка представляет собой запись
полинома
коэффициентами
по возрастанию степени. Остальные
строки — циклические сдвиги первой
строки.
Проверочная
матрица:
,
где
i-ый столбец, начиная с 1-ого, представляет
собой остаток от деления
на
полином
,
записанный по возрастанию степеней,
начиная сверху.
Так,
например, 4-ий столбец получается
,
или в векторной записи
.
Легко
убедиться, что
.