12.Матричное кодирование и декодирование.
Матричное кодирование
Ранее
каждая схема кодирования описывалась
таблицами, задающими кодовое слово
длины
для
каждого исходного слова длины
.
Для блоков большой длины этот способ
требует большого объема памяти и поэтому
непрактичен. Например, для
-кода
потребуется
бит.
Гораздо
меньшего объема памяти требует матричное
кодирование. Пусть
матрица
размерности
,
состоящая из элементов
,
где
-
это номер строки, а
-
номер столбца. Каждый из элементов
матрицы
может
быть либо 0, либо 1. Кодирование реализуется
операцией
или
,
где кодовые слова рассматриваются как
векторы, т.е как матрицы-строки размера
.
Пример.
Рассмотрим следующую
-матрицу:
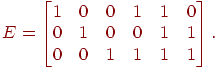Тогда
кодирование задается такими отображениями:
,
,
,
,
,
,
,
.
Рассмотренный пример показывает
преимущества матричного кодирования:
достаточно запомнить
кодовых
слов вместо
слов.
Это общий факт.
Кодирование не должно
приписывать одно и то же кодовое слово
разным исходным сообщениям. Простой
способ добиться этого состоит в том,
чтобы
столбцов
(в предыдущем примере - первых) матрицы
образовывали
единичную матрицу. При умножении любого
вектора на единичную матрицу получается
этот же самый вектор, следовательно,
разным векторам-сообщениям будут
соответствовать разные вектора
систематического кода.
Матричные
коды называют также линейными кодами.
Для линейных
-кодов
с минимальным расстоянием Хэмминга
существует
нижняя граница Плоткина (Plotkin)1)
для минимального количества контрольных
разрядов
при
,
13.Мажоритарное декодирование, мажоритарный кодер и декодер
Мажоритарный метод, давно и широко используется, и состоит в следующем:
Каждое сообщение ограниченной длины передается несколько раз, чаще всего три раза.
0001
1 0011 1
0001
Принимаемые сообщения запоминаются, а потом производится их поразрядное сравнение.
Суждение о правильности передачи выносится по совпадению большинства из принятой информации методом «два из трех».
Стремление
создать наиболее простой двоичный
декодер привело к созданию так называемых
мажоритарных декодеров, которые являются
наипростейшими и могут быть использованы
для декодирования двоичных кодов большой
длины.
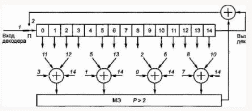
Он состоит из:
кольцевого регистра сдвига длины n = 15,
четырех четырехвходовых сумматоров по mod 2, мажоритарного элемента (МЭ) двухвходового сумматора по mod 2, непосредственно исправляющего ошибки.
14.Метод синдромного декодирования.
Коды
Хэмминга имеют кодовое расстояние
,
исправляют все однократные ошибки или
обнаруживают двукратные, т.е.
,
.
Зависимости проверочных символов от
информационных выбраны так, что каждой
однократной ошибке соответствует свое
ненулевое значение синдрома. Поэтому
для кодов Хэмминга число ненулевых
синдромов равно числу символов в кодовых
комбинациях (числу однократных ошибок):
|
(5.24) |
.
Следовательно,
для кодов Хэмминга достигается нижняя
граница числа
избыточных
символов, а сами коды являются совершенными.
Примеры кодов: (3, 1,3), (7,4, 3), (15, И, 3), (31,26,
3), (63, 57, 3),....
Единственный код Голея (23, 12, 7) завершает ряд совершенных кодов.
Расширенный
код Хэмминга образуется из совершенного
путем добавления общей проверки на
четность, т. е. проверочного символа,
равного сумме всех символов кода
Хэмминга. Код имеет кодовое расстояние
,
что позволяет исправить все однократные
и одновременно обнаружить все двукратные
ошибки. Такой режим целесообразен, в
частности, в системах передачи информации
с обратной связью.
При
добавлении проверочного символа длина
кода становится четной, а соотношение
(5.24) преобразуется к виду
.
Расширенные коды Хэмминга образуют
ряд: (4, 1,4), (8,4,4), (16, 11,4), (32, 26,4), (64,57,4),....
Коды
этого вида относятся к квазисовершенным,
т.е. исправляющим все ошибки кратности
по
включительно
и часть ошибок кратности
