1. Криволинейный интеграл 1-го рода.
Рисунок 13 |
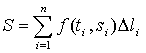
Определение. Предел 
, если
он существует, называется криволинейным
интегралом 1-го
родаот
функции f (x,y)
по кривой L и
обозначается
(20)
В случае замкнутой кривой L выбирается произвольная точка на кривой, которая принимается за концевые точки А, В, и криволинейный интеграл 1-го рода определяется аналогично случаю незамкнутой кривой.
Теорема (достаточное условие существования интеграла). Если функция f (x,y) непрерывна на кривой L за исключением, быть может, конечного числа точек и ограничена на L, то криволинейный интеграл 1-го рода (20) существует.
Некоторые свойства криволинейного интеграла 1-го рода. Для криволинейных интегралов 1-го рода выполняются свойствалинейности и аддитивности
1) L=
, где L длина
кривой L.
2) Криволинейный интеграл 1-го рода (20) не зависит от ориентации кривой L. Это значит, что интеграл не зависит от того, какая из концевых точек А и В является начальной точкой кривой.
Физический смысл криволинейного интеграла 1-го рода. Пусть L кривая с линейной плотностью массы (х, у). Тогда масса кривой равна
(21)
Замечание. Криволинейный интеграл 1-го рода аналогично определяется и для пространственной кривой.
2.Вычисление криволинейного интеграла 1-го рода.
Пусть кривая L задана параметрическими уравнениями x = (t), y= (t), ≤ t ≤,
где (t), (t) непрерывно дифференцируемые на отрезке [, ] функции. Тогда
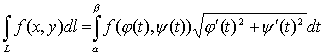. (22)
Пусть кривая L задана явно уравнением y=g (x), a≤ x ≤b,
где g (x) непрерывно дифференцируемая на [a, b] функция. Тогда
. (23)
|
|
3. Криволинейный интеграл 2-го рода.
Рассмотрим ориентированную незамкнутую кривую L = АВ в плоскости хОу с началом в точке А и концом в точке В; z=f (x,y) функция, определенная на кривой L. Разобьем кривую L последовательными точками
А0=А, А1, А2, . . . , Аn=В
на дуги 1= А0А1, 2= А1А2, . . . , n= Аn-1Аn и на дуге i выберем произвольную точку Мi(ti , si) (i = 1, 2, . . . , n) (рис. 16). Обозначим xi = xi xi1 , yi = yi yi1, а наибольшую из длин дуг i (i = 1,2, . . . , n).
Составим интегральную сумму функции f (x,y) по кривой L относительно х
Определение. Предел 
, если
он существует, называется криволинейным
интегралом 2-го
рода от
функции f (x,y)
по кривой L
относительно х и
обозначается
Рисунок 16 |
(24)
В случае замкнутой кривой L выбирается произвольная точка на кривой, которая принимается за концевые точки А, В, и криволинейный интеграл 2-го рода определяется аналогично случаю незамкнутой кривой.
Теорема (достаточное условие существования интеграла). Если функция f (x,y) непрерывна на кривой L за исключением, быть может, конечного числа точек и ограничена на L, то криволинейный интеграл 2-го рода (24) существует.
Некоторые свойства криволинейного интеграла 2-го рода. Для криволинейных интегралов 2-го рода выполняются свойства линейности и аддитивности (см. аналогичные свойства для тройного интеграла в п. 10).
Свойство антиориентированности
.
Это свойство связано с тем, что при изменении направления обхода кривой все приращения xi и, следовательно, интегральная сумма Sx изменяют знак.
Аналогично определяется криволинейный интеграл 2-го рода от функции g(x,y) по кривой L относительно у
,
где 
.
Пусть на ориентированной кривой L определены две функции f (x, y) и g (x, y). Тогда сумма интегралов (24) и (25) называется общим криволинейным интегралом 2-го рода от функций f (x,y) и g (x,y) по кривой L и обозначается
(26)
Физический смысл криволинейного интеграла 2-го рода. Пусть
сила,
действующая на материальной
точку М(x, y) ориентированной
кривой L. Тогда
работа, совершаемая силой 
при
перемещении точки М вдоль
ориентированной кривой L, равна
(27)
Замечание. Криволинейный интеграл 2-го рода аналогично определяется и для пространственной ориентированной кривой.
Площадь плоской фигуры. Пусть простая замкнутая кривая3 L ориентирована “против часовой стрелки”, D область, ограниченная кривой L. Тогда площадь области D равна
(28)