
- •2. Диодный ключ. Работа в статическом и динамическом режимах.
- •3. Собственный и примесные проводники.
- •4.Типы полупроводниковых диодов. Параметры Диодов. Типы полупроводниковых диодов:
- •6. Параметрический стабилизатор напряжения.
- •7. Закон распределения носителей в зонах полупроводника. Функция Ферми – Дирака.
- •8. Туннельный диод.
- •9. Работа выхода.
- •10. Варикап.
- •11. Генерация и рекомбинация. Виды пробоев.
- •Vt может работать в 4 режимах, в зависимости от напряжения на его
- •13. Контакты полупроводник – металл.
- •14. Технология изготовления транзисторов.
- •15. Емкости p-n перехода. Схемы замещения p-n перехода.
- •16. Энергетические диаграммы транзистора при включении с общей базой.
- •8. Чрезмерное большое выходное сопротивление затрудняет согласование с нагрузкой. 17. Лавинно-пролетный диод. Применение.
- •18. Схемы включения транзисторов. Схема замещения транзисторов.
- •Схемы замещения транзистора.
- •19. Принцип работы фотоприемников.
- •20. Входные и выходные характеристики транзисторов при различных схемах включения.
- •21. Фоторезисторы. Схемы включения.
- •22. Емкости транзистора. Частотные характеристики транзистора.
- •23. Представление транзистора в виде четырехполюсника и системы статистических параметров.
- •24. Фотодиоды. Схемы включения фотодиодов.
- •25. Определение h-параметров по статическим характеристикам транзистора. Страница 66 методичка по фоэт.
- •26. Лавинные фотодиоды.
- •27. Фототранзисторы. Схемы включения.
- •28. Динамический режим работы транзистора.
- •29. Фототиристоры. Характеристики.
- •30. Транзисторный ключ. Основная схема, увеличение быстродействия.
- •31. Ненасыщенный транзисторный ключ.
- •32. Квантовая система. Энергетические уровни.
- •33. Спонтанное и индуцированное излучение. Трехуровневая квантовая система.
- •34. Высокочастотные транзисторы. Технология изготовления, свойства. 35. Полевые транзисторы. Разновидности. Схемы включения.
- •36. Основы работы полупроводниковых лазеров.
- •37. Схема действия полупроводникового инжекционного лазера. Инжекционный лазер представляет собой инжекционный p - n переход, в котором
- •38. Полевые транзисторы с управляющим p-n переходом.
- •40. Динисторы. Структура, схема замещения, вах.
- •Чем отличается динистор от полупроводникового диода?
- •Принцип работы динистора.
- •Вах динистора.
- •41. Разновидности мдп-транзисторов, статические характеристики.
- •42. Тиристоры и их классификация.
- •43. Полевые транзисторы с изолированным затвором и индуцированным каналом, устройство, вах, основные особенности.
- •44. Характеристики переходных процессов включения тиристоров и их особенности.
- •45. Полевые транзисторы с изолированным затвором и встроенным каналом, устройство, семейство вах, основные особенности.
- •47. Биполярные транзисторы с изолированным затвором (igbt), их устройство и основные особенности.
- •Применение
- •48. Критическая скорость нарастания прямого напряжения на тиристоре. Эффект du/dt. Критическая скорость нарастания напряжения в закрытом состоянии.
- •49. Ненасыщенный транзисторный ключ с нелинейной обратной связью.
- •51. Транзисторный ключ с форсирующим конденсатором.
- •52. Включение тиристорной структуры сигналом управления. Параметры процесса включения тиристора.
- •53. Методы улучшения импульсных и частотных свойств биполярных транзисторов.
- •54. Оособенности процесса выключении тиристора. Области применения тиристора.
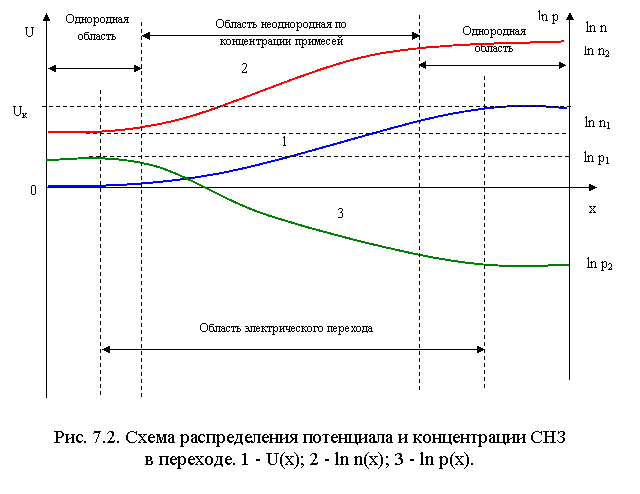
- •55. Распределение электрического потенциала в объеме полупроводника.
54. Оособенности процесса выключении тиристора. Области применения тиристора.
Смотри вопрос 46.
55. Распределение электрического потенциала в объеме полупроводника.
Выделим мысленно бесконечно тонкий слой dx электронного газа, заключенный между плоскостями I и II с координатами х и x+dx. Этот слой будет испытывать со стороны окружающего электронного газа давление Р1 слева и Р2 справа. Давление газа, как известно, равно nkT, где n- концентрация частиц этого газа. Обозначим концентрацию электронов в плоскости 1 через n1 а в плоскости II через n2. Тогда разность давлений ∆Р на рассматриваемый слой будет равна:
![]() (7.1)
(7.1)
Сила перепада давлений, действующая на слой dx, будет равна:
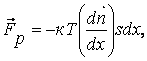 (7.2)
(7.2)
где s- площадь границ слоя. Знак " - " показывает, что эта сила противоположна направлению вектора градиента концентрации электронов.
Определим силу электрического поля, действующую на тот же слой. Электрический заряд слоя ∆Q равен:
![]() (7.3)
(7.3)
Электрическая
сила ![]() ,
действующая на слой, будет равна:
,
действующая на слой, будет равна:
![]() (7.4)
(7.4)
В состоянии равновесия сумма сил, действующих на слой, равна нулю. Следовательно:
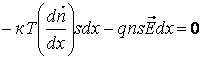
или
![]() (7.5)
(7.5)
Так
как![]() ,
то
,
то
![]() (7.6)
(7.6)
Решая это дифференциальное уравнение, получим:
 (7.7)
(7.7)
Рассуждая аналогично в отношении дырочного газа, найдем, что
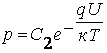 (7.8)
(7.8)
Константы интегрирования С1 и С2 определяются как всегда из граничных условий. Начало координат мы поместили в глубине однородной области I полупроводника. Здесь выполняется условие локальной электрической нейтральности и поле отсутствует. Примем потенциал этой области в окрестности начала координат равным нулю. Тогда, подставляя в (7.7) и (7.8) значения x = 0; U = 0; n = n1; p = p1, получим С1= n1, С2 = р1. Следовательно:
 (7.9)
(7.9)
 (7.10)
(7.10)
Таким образом, концентрация СНЗ и потенциал в электрическом переходе связаны между собой экспоненциальной зависимостью.
Распределение потенциала в переходе определим, решив уравнение Пуассона. Плотность пространственного заряда в любом слое равна:
![]() (7.11)
(7.11)
или, учитывая (7.9) и (7.10):
 (7.12)
(7.12)
Следовательно, уравнение Пуассона будет иметь вид:
 (7.13)
(7.13)
Поскольку распределение примесей, т.е. (Nd-Na) = ƒ(х) известно, то, решая (7.13), найдем U = U(x).
Так как соотношения (7.9) и (7.10) должны быть справедливы для любого элемента объема полупроводника, то, применяя их для второй однородной области, где концентрации электронов и дырок соответственно равны n2 и p2 получим, что потенциал этой области U2 равен:
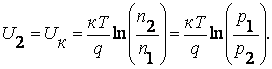 (7.14)
(7.14)
Разность потенциалов на концах электрического перехода пропорциональна логарифму отношения концентраций однотипных СНЗ в однородных областях полупроводника, разделенных переходом. Эта разность называется контактной разностью потенциалов перехода.
Деба́евская длина (дебаевский радиус) — расстояние, на которое распространяется действие электрического поля отдельного заряда в нейтральной среде, состоящей из положительно и отрицательно заряженных частиц (плазма, электролиты). Вне сферы радиуса дебаевской длины электрическое поле экранируется в результате поляризации окружающей среды (поэтому это явление еще называют экранировкой Дебая).
Дебаевская длина определяется формулой (СГС):
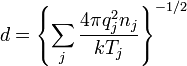
(СИ) :
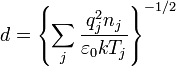
где: ![]() ,
, ![]() ,
, ![]() — электрический
заряд, концентрация
частиц и температура частиц
типа
— электрический
заряд, концентрация
частиц и температура частиц
типа ![]() ;
; ![]() ,
, ![]() — постоянная
Больцмана и диэлектрическая
проницаемость вакуума. Суммирование
идет по всем сортам частиц, при этом
должно выполняться условие нейтральности:
— постоянная
Больцмана и диэлектрическая
проницаемость вакуума. Суммирование
идет по всем сортам частиц, при этом
должно выполняться условие нейтральности: ![]() .
Важным параметром среды является число
частиц в сфере радиуса дебаевской длины:
.
Важным параметром среды является число
частиц в сфере радиуса дебаевской длины:
56. Определение h-параметров по статическим характеристикам транзисторов.








58. Импульсные диоды.


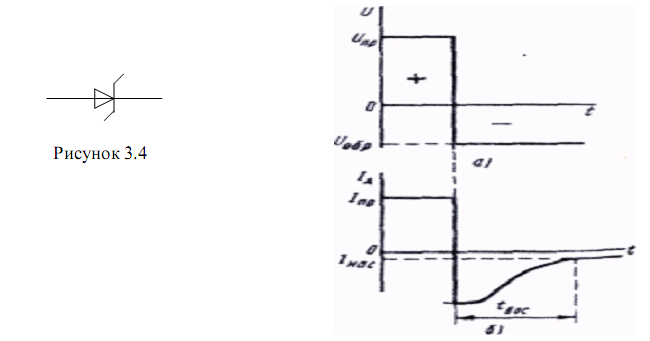 59.
Диффузионный и дрейфовый токи в
полупроводниках.
59.
Диффузионный и дрейфовый токи в
полупроводниках.

60. Выпрямительные диоды.


Directed by V.I.P. Big Thanks All For a Work.
