Ргр2 Корреляционно-регрессионный анализ
Цель работы: исследование парной корреляции,
формирование модели множественной регрессии,
оценка адекватности модели,
оценка влияния факторных признаков на результативный признак.
1. Исследование парной корреляции
Парная корреляция - зависимость между двумя признаками (результативным и одним из факторных). Порядок исследования парной корреляции следующий:
1.1. Определяется характер связи
Для того, чтобы проверить, как проявляется связь между двумя переменными (признаками), нужно построить график-поле корреляции.
Поле
корреляции - это поле точек, на котором
каждая точка соответствует
единице совокупности; ее координаты
определяются значениями признаков
х и у, И по характеру расположения точек
на поле корреляции делают вывод
о наличии или отсутствии связи, о
характере связи (линейная или нелинейная,
а если связь линейная - то прямая или
обратная). Для того чтобы разобраться,
как проявляется изучаемая связь у разных
единиц, можно разделить поле
корреляции на 4 области линиями
и
(
см.рис.1)
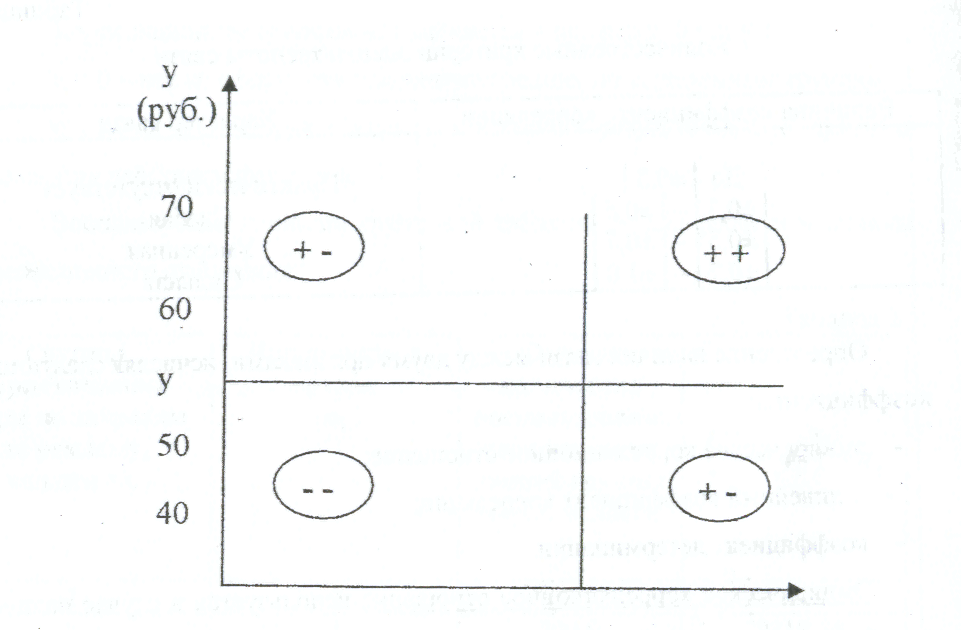
Рис.1. Поле корреляции.
Когда имеет место
прямая связь, то большинство рассматриваемых
точек попадают в область (++) или (- -). В
области (++) отклонения
и
положительны,
а в области (- -) произведение отклонений
и
положительно,
что приведет к положительному знаку
коэффициента парной корреляции.
1.2. Оценка связи между количественными признаками
Теснота связи между количественными признаками определяется, исчисляя следующие показатели, значения которых сопоставляют с табличными (табл. 1).
Таблица 1.
Количественные критерии оценки тесноты связи.
Величина коэффициента корреляции |
Характер связи |
До |±0,3| |±0,3| - |±0,5| |±0,5| - |±0,7| |±0,7| - |±1,0| |
Практически отсутствует Слабая Умеренная Сильная |
Определения наличия связи между двумя признаками, исчисляя следующие коэффициенты: линейный (парный) коэффициент корреляции;
коэффициент детерминации.
А) Расчет линейного коэффициента корреляции выполняется следующим образом:
Определяется величина коэффициента корреляции rxy (r) , дается его оценка.
или 
где 
-
среднее значение соответствующего
факторного признака;
- среднее значение
результативного признака;
- среднее
квадратическое отклонение
соответствующего факторного
признака;
- среднее квадратическое отклонение
результативного признака;
n - число наблюдений.
Линейный коэффициент корреляции изменяется в пределах от -1 до 1: -
Если знаки отклонений от средних совпадают, то связь прямая (гху >0), если знаки отклонений не совпадают, то связь обратная (гху<0). При этом интерпретацию выходных значений коэффициента корреляции можно представить в табл.2 .
Таблица 2.
Оценка линейного коэффициента корреляции
Значение линейного коэффициента связи |
Характер связи |
Интерпретация связи |
r = 0 |
Отсутствует |
— |
0 < г< 1 |
Прямая |
С увеличением х увеличивается у |
-1 < г<0 |
Обратная |
С увеличением х уменьшается у и наоборот |
r = 1 |
Функциональная |
Каждому значению факторного признака строго соответствует одно значение результативного признака |
Пример:
на основе данных табл.3.рассчитываем коэффициент парной корреляции между ценой товара и дальностью перевозки.
Таблица 3
-
№ п/п
xi
yi
1
1
4
-3
-8
24
9
64
2
2
5
-2
-7
14
4
49
3
3
10
-1
-2
2
1
4
4
4
12
0
0
0
0
0
5
5
15
1
3
3
1
9
6
6
17
2
5
10
4
25
7
7
21
3
9
27
9
81
Итого
80
28
232
-
среднее значение факторного признака
x;
-
среднее значение результативного
признака y;
Полученное значение коэффициента корреляции показывает, что связь между ценой товара и дальностью его перевозки является очень тесной.
При использовании для определения тесноты связи линейного коэффициента корреляции производится оценка его значимости :