Контур с током в однородном магнитном поле.

.

Покажем, что момент сил, действующих на контур с током в магнитном поле не зависит от точки, относительно которой мы его считаем: Момент относительно какой-то точки внутри контура O . Момент относительно какой-то другой точки внутри контура . Здесь – радиус-вектор элемента контура , на который действует сила относительно точки O, – радиус-вектор того де элемента относительно точки – радиус вектор точки относительно точки O.

П усть . Тогда . Аналогично , но , где – площадь полоски. Таким образом, .

Дипольный магнитный момент контура с током .

.

Пусть теперь . Тогда .

Магнитное поле в веществе

Если проводники создают магнитное поле , то в веществе . Это говорит о том, что вещества намагничиваются. В отсутствие магнитного поля ориентация витков с током в веществе (орбит электронов вокруг атомов) хаотично, следовательно . При введении вещества в магнитное поле они начинают ориентироваться вдоль него (поляризовываться) и тогда .

Вектор намагниченности .

Каждый атом вещества в соответствии с моделью Бора можно представить как маленький виток с током. Тогда , где – плотность макроскопических токов, – плотность молекулярных токов. Вычислим сумму молекулярных токов, охватываемых некоторым контуром: . Сумма токов, пронизанных отрезком равна , где 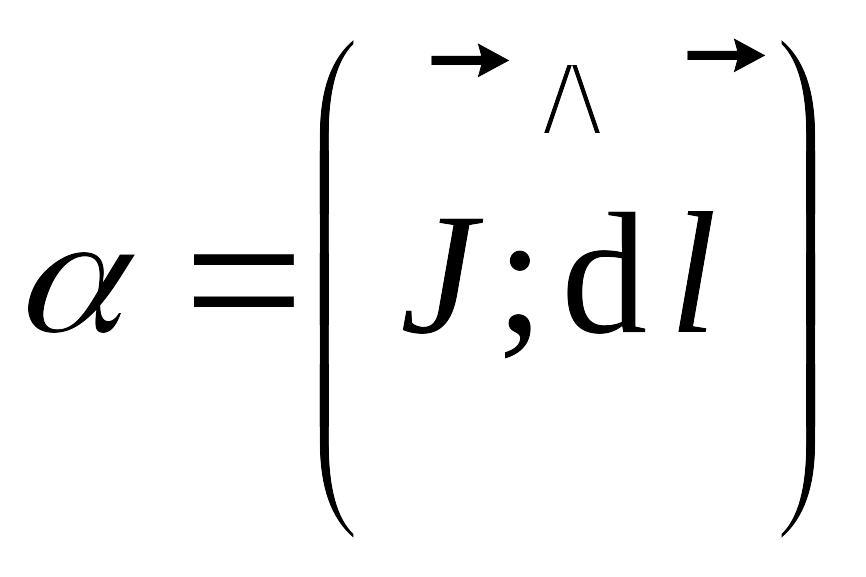, – ток одного витка, S – его площадь, n – концентрации атомов. . В то же время . Т.к. , то 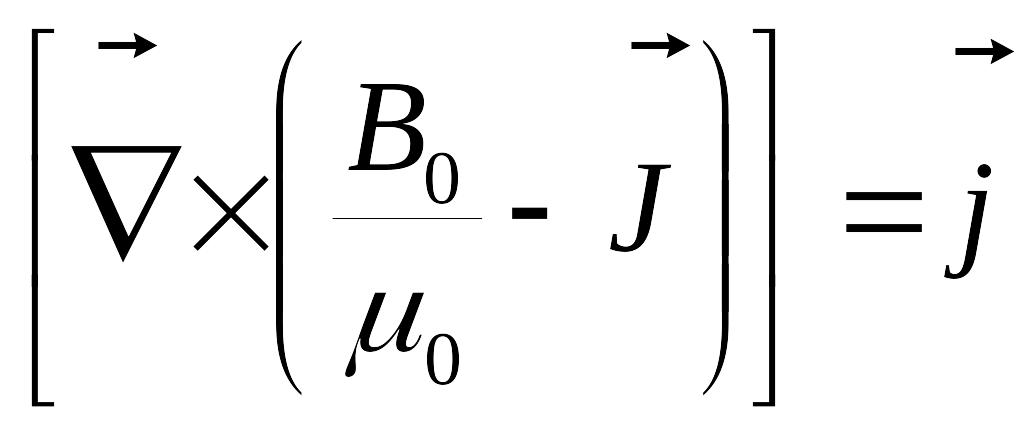. Выражение называют вектором напряжённости. . Циркуляция ; , где ­ – магнитная восприимчивость. , где – относительная магнитная проницаемость.

Это справедливо только в изотропных случаях. В противном случае  – тензор.

Вещества, проявляющие магнитные свойства в магнитном поле, называются магнетиками.

Условия на границе двух магнетиков.

. Рассмотрим теперь такой же контур: , где a – сторона контура, параллельная границе раздела, b – перпендикулярная ей. .

Для диамагнетиков ( , где – объём одного моля); для парамагнетиков , для ферромагнетиков .

Магнитомеханические явления

Модель атома Бора ( – момент инерции электрона относительно ядра атома):

– магнитомеханическое отношение (гиромагнитное отношение).

Эксперимент показал, что – следовательно, у электрона есть собственный механический момент (спин): . – магнетон Бора.

Диамагнетизм

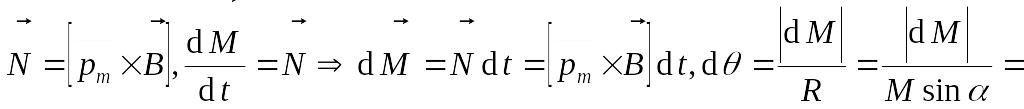
М омент силы . Таким образом, скорость прецессии – Ларморова частота прецессии не зависит от радиуса орбиты, скорости электрона и угла наклона орбиты к , следовательно, любой электрон в веществе прецессирует одинаково. – ток, который при этом создаётся, , где r – радиус прецессии электрона. Среднее значение , где R – радиус электронной орбиты. Тогда . Диамагнитные свойства проявляются только у тех веществ, атомы которых не обладают собственным магнитным моментом.

Парамагнетизм

. Работа при повороте магнитного момента на угол . Потенциальная энергия . Если парамагнетик не находится в магнитном поле, то ориентирован случайным образом. При помещении его в магнитное поле идут два процесса: выстраивание вдоль и разрушение этого выстраивания. Количество частиц, находящихся в

потенциальном поле с энергией с координатами . Вероятность найти в некотором угле , где A ­ нормировочная константа. Введём сферическую систему координат. Тогда ( – вертикальный угол в сферической системе координат, характеризующий направление телесного угла ), 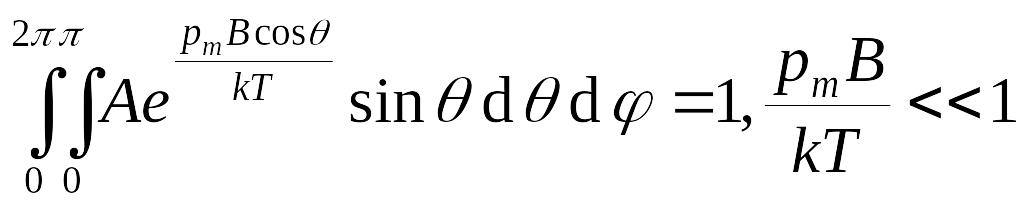. Пусть . Тогда и , следовательно, .

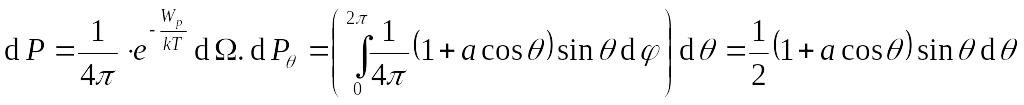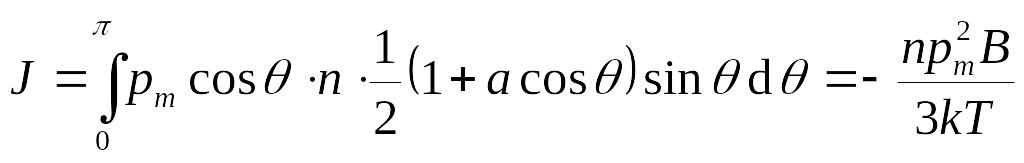Количество молекул, у которых направлен под углом  к , где n – концентрация молекул в единице объёма вещества. , , – закон Кюри.